Влияние кубических и катмулловых сплайнов на изображение

Question

Я пытаюсь реализовать какую-то функцию, как показано ниже

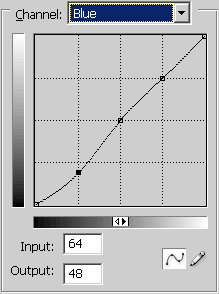
Для этого я пытаюсь использовать Cubic interpolation а также Catmull interpolation (отметьте оба по отдельности, чтобы сравнить лучший результат), что я не понимаю, так это то, как эти интерполяции отражаются на изображении и как мы можем получить значения этих точек, где мы щелкнули, чтобы установить эту кривую? и нужно ли нам определять функцию этих черных точек на изображении отдельно?

Я получаю помощь от этих ресурсов

Источник 1

Источник 2

Приблизительно такой же фокус

редактировать

int main (int argc, const char** argv)
{
Mat input = imread ("E:\\img2.jpg");
for(int i=0 ; i<input.rows ; i++)
{
    for (int p=0;p<input.cols;p++)
    {
        //for(int t=0; t<input.channels(); t++)
    //{

        input.at<cv::Vec3b>(i,p)[0] = 255*correction(input.at<cv::Vec3b>(i,p)[0]/255.0,ctrl,N);  //B
        input.at<cv::Vec3b>(i,p)[1] = 255*correction(input.at<cv::Vec3b>(i,p)[1]/255.0,ctrl,N);  //G
        input.at<cv::Vec3b>(i,p)[2] = 255*correction(input.at<cv::Vec3b>(i,p)[2]/255.0,ctrl,N);  //R
    //}
    }
}

imshow("image" , input);
waitKey();
}

Answer 1

Так что, если ваши контрольные точки всегда находятся на одной и той же координате х
и линейно распределены по всему диапазону, то вы можете сделать это так:

//---------------------------------------------------------------------------
const int N=5;      // number of control points (must be >= 4)
float ctrl[N]=      // control points y values initiated with linear function y=x
    {           // x value is index*1.0/(N-1)
    0.00,
    0.25,
    0.50,
    0.75,
    1.00,
    };
//---------------------------------------------------------------------------
float correction(float col,float *ctrl,int n)
    {
    float di=1.0/float(n-1);
    int i0,i1,i2,i3;
    float t,tt,ttt;
    float a0,a1,a2,a3,d1,d2;
    // find start control point
    col*=float(n-1);
    i1=col; col-=i1;
    i0=i1-1; if (i0< 0) i0=0;
    i2=i1+1; if (i2>=n) i2=n-1;
    i3=i1+2; if (i3>=n) i3=n-1;
    // compute interpolation coefficients
    d1=0.5*(ctrl[i2]-ctrl[i0]);
    d2=0.5*(ctrl[i3]-ctrl[i1]);
    a0=ctrl[i1];
    a1=d1;
    a2=(3.0*(ctrl[i2]-ctrl[i1]))-(2.0*d1)-d2;
    a3=d1+d2+(2.0*(-ctrl[i2]+ctrl[i1]));
    // now interpolate new colro intensity
    t=col; tt=t*t; ttt=tt*t;
    t=a0+(a1*t)+(a2*tt)+(a3*ttt);
    return t;
    }
//---------------------------------------------------------------------------

Он использует 4-точечную 1D кубическую интерполяцию (по этой ссылке в моем комментарии выше), чтобы получить новый цвет, просто сделайте это:

new_col = correction(old_col,ctrl,N);

вот как это выглядит:

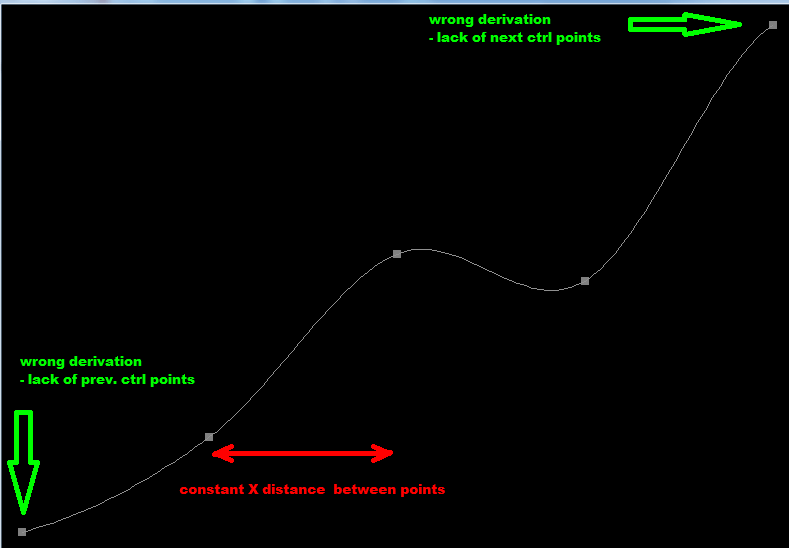
зеленые стрелки показывают ошибку деривации (всегда только в начальной и конечной точке всей кривой). Это можно исправить, добавив еще 2 контрольные точки, одну до и одну после всех остальных...

[Заметки]

цветовая гамма < 0.0 , 1.0 > так что если вам нужен другой, то просто умножьте результат и разделите входные данные...

[edit1] начало / конец деривации немного исправлено

float correction(float col,float *ctrl,int n)
    {
    float di=1.0/float(n-1);
    int i0,i1,i2,i3;
    float t,tt,ttt;
    float a0,a1,a2,a3,d1,d2;
    // find start control point
    col*=float(n-1);
    i1=col; col-=i1;
    i0=i1-1;
    i2=i1+1; if (i2>=n) i2=n-1;
    i3=i1+2;
    // compute interpolation coefficients
    if (i0>=0) d1=0.5*(ctrl[i2]-ctrl[i0]); else d1=ctrl[i2]-ctrl[i1];
    if (i3< n) d2=0.5*(ctrl[i3]-ctrl[i1]); else d2=ctrl[i2]-ctrl[i1];
    a0=ctrl[i1];
    a1=d1;
    a2=(3.0*(ctrl[i2]-ctrl[i1]))-(2.0*d1)-d2;
    a3=d1+d2+(2.0*(-ctrl[i2]+ctrl[i1]));
    // now interpolate new colro intensity
    t=col; tt=t*t; ttt=tt*t;
    t=a0+(a1*t)+(a2*tt)+(a3*ttt);
    return t;
    }

[edit2] просто некоторые разъяснения по коэффициентам

все они получены из следующих условий:

y(t) = a0 + a1*t + a2*t*t + a3*t*t*t // direct value
y'(t) = a1 + 2*a2*t + 3*a3*t*t        // first derivation

теперь у вас есть очки y0,y1,y2,y3 поэтому я выбрал это y(0)=y1 а также y(1)=y2 который дает непрерывность c0 (значение одинаково в точках соединения между кривыми)
теперь мне нужна непрерывность c1, поэтому я добавляю y'(0) должен быть таким же, как y'(1) из предыдущей кривой.
за y'(0) Я выбираю среднее направление между точками y0,y1,y2
за y'(1) Я выбираю среднее направление между точками y1,y2,y3
Они одинаковы для следующих / предыдущих сегментов, поэтому этого достаточно. Теперь соберите все это вместе:

y(0)  = y0           = a0 + a1*0 + a2*0*0 + a3*0*0*0
y(1)  = y1           = a0 + a1*1 + a2*1*1 + a3*1*1*1
y'(0) = 0.5*(y2-y0) = a1 + 2*a2*0 + 3*a3*0*0
y'(1) = 0.5*(y3-y1) = a1 + 2*a2*1 + 3*a3*1*1

И решить эту систему уравнений (a0,a1,a2,a3 = ?), Вы получите то, что у меня есть в исходном коде выше. Если вам нужны разные свойства кривой, просто создайте разные уравнения...

[edit3] использование

pic1=pic0; // copy source image to destination pic is mine image class ...
for (y=0;y<pic1.ys;y++) // go through all pixels
 for (x=0;x<pic1.xs;x++)
    {
    float i;
     //  read, convert, write pixel 
    i=pic1.p[y][x].db[0]; i=255.0*correction(i/255.0,red control points,5); pic1.p[y][x].db[0]=i;
    i=pic1.p[y][x].db[1]; i=255.0*correction(i/255.0,green control points,5); pic1.p[y][x].db[1]=i;
    i=pic1.p[y][x].db[2]; i=255.0*correction(i/255.0,blue control points,5); pic1.p[y][x].db[2]=i;
    }

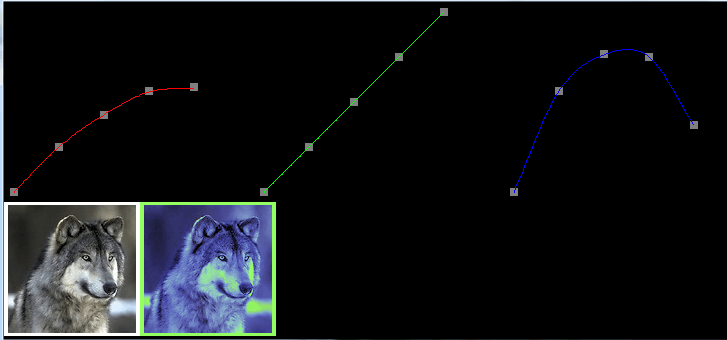
На вершине есть контрольные точки в R,G,B, Слева внизу оригинальное изображение, а справа внизу исправленное изображение.