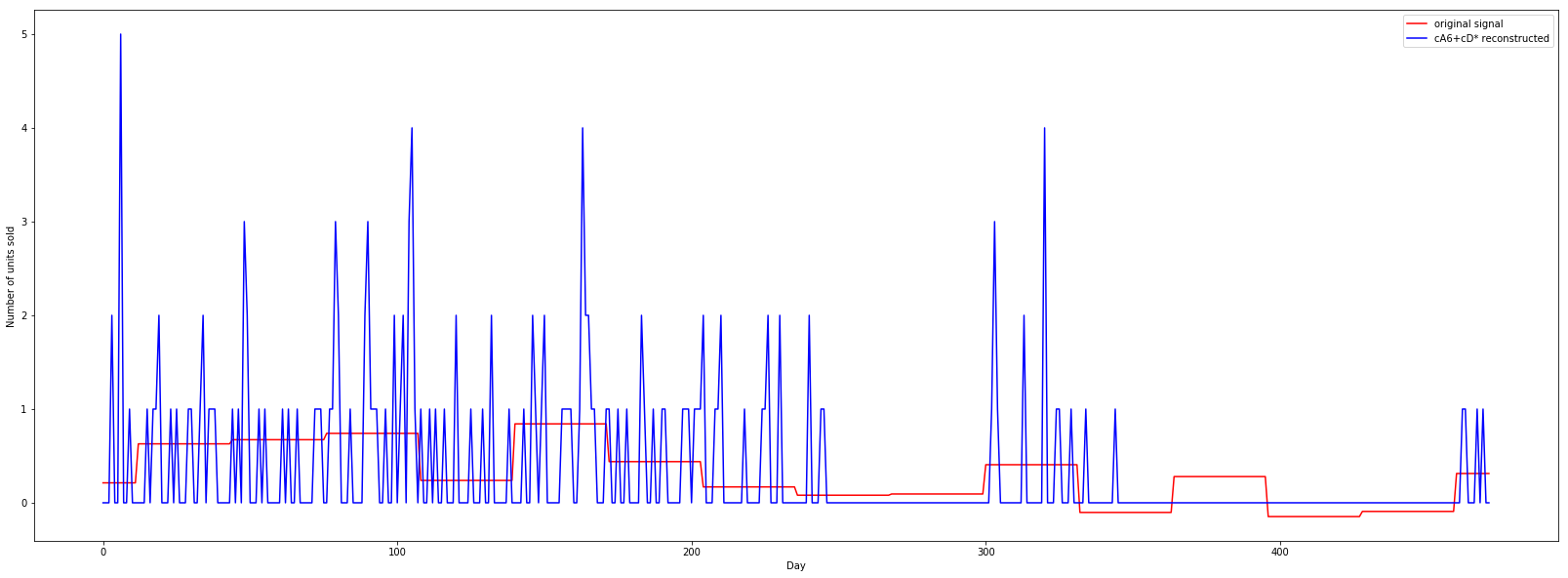
Реконструкция сигнала Пивавелета

Question

Я пытаюсь понять концепцию вейвлетов, используя библиотеку pywavelet. Моим первым шагом было посмотреть, как я могу восстановить данный входной сигнал, используя вейвлет-коэффициенты. Пожалуйста, смотрите мой код ниже:

db1 = pywt.Wavelet('db1')
cA6, cD6,cD5, cD4, cD3, cD2, cD1=pywt.wavedec(data, db1, level=6)
cA6cD_approx = pywt.upcoef('a',cA6,'db1',take=n, level=6) +   pywt.upcoef('d',cD1,'db1',take=n, level=6)\
 +pywt.upcoef('d',cD2,'db1',take=n, level=6) +  pywt.upcoef('d',cD3,'db1',take=n, level=6) + \
  pywt.upcoef('d',cD4,'db1',take=n, level=6) + pywt.upcoef('d',cD5,'db1',take=n, level=6) + \
  pywt.upcoef('d',cD6,'db1',take=n, level=6)

plt.figure(figsize=(28,10))
p1, =plt.plot(t, cA6cD_approx,'r')
p2, =plt.plot(t, data, 'b')
plt.xlabel('Day')
plt.ylabel('Number of units sold')
plt.legend([p2,p1], ["original signal", "cA6+cD* reconstructed"])
plt.show()

Это дало следующий сюжет:

Теперь, когда я использовал waverec() Метод восстановления сигнала был достаточно точным. Пожалуйста, смотрите график ниже: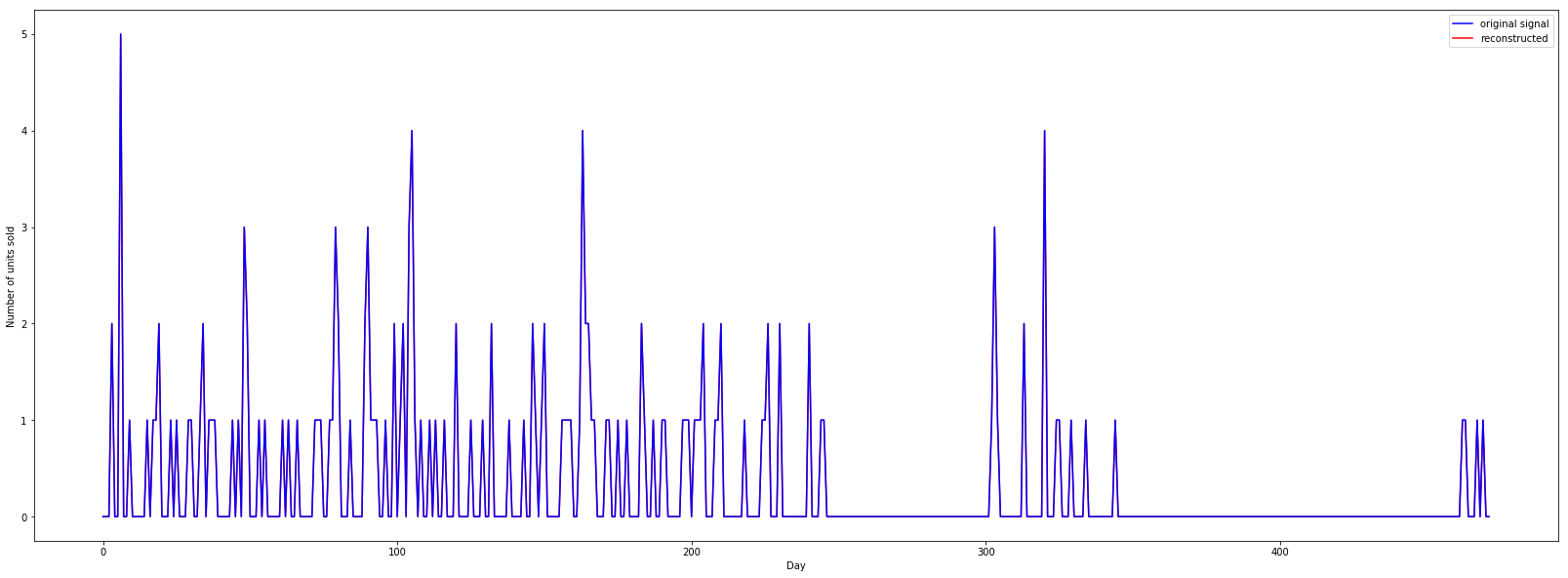

Может кто-нибудь объяснить, пожалуйста, разницу между двумя методами реконструкции?

Answer 1

Оба они являются обратным дискретным вейвлет-преобразованием "upcoef" - это прямая реконструкция с использованием коэффициентов, в то время как "waverec" - это многоуровневое 1D-обратное вейвлет-преобразование, выполняющее почти одно и то же, но делающее так, чтобы выстроить коэффициенты и быть более эффективными при разработке.

Answer 2

Я немного изменил, особенно настройки для "уровня". Из сюжета вы увидите два способа реконструкции, которые дадут одинаковый результат.

import numpy as np
import pywt
import matplotlib.pyplot as plt

data = np.loadtxt('Mysample_test.txt')
n = len(data)
wl = pywt.Wavelet("db1")
coeff_all = pywt.wavedec(data, wl, level=6)
cA6, cD6,cD5, cD4, cD3, cD2, cD1= coeff_all
omp0 = pywt.upcoef('a',cA6,wl,level=6)[:n]
omp1 = pywt.upcoef('d',cD1,wl,level=1)[:n]
omp2 = pywt.upcoef('d',cD2,wl,level=2)[:n]
omp3 = pywt.upcoef('d',cD3,wl,level=3)[:n]
omp4 = pywt.upcoef('d',cD4,wl,level=4)[:n]
omp5 = pywt.upcoef('d',cD5,wl,level=5)[:n]
omp6 = pywt.upcoef('d',cD6,wl,level=6)[:n]

#cA6cD_approx = omp0 + omp1 + omp2 + omp3 + omp4+ omp5 + omp6
#plt.figure(figsize=(18,9))
recon = pywt.waverec(coeff_all, wavelet= wl)
p1, =plt.plot(omp0 + omp6 + omp5 + omp4 + omp3 + omp2 + omp1,'r')
p2, =plt.plot(data, 'b')
p3, =plt.plot(recon, 'y')

plt.xlabel('Day')
plt.ylabel('Number of units sold')
plt.legend([p3,p2,p1], ["waverec reconstructed","original signal", "cA6+cD* reconstructed"])
plt.show()

Answer 3

Функция wavedec выполняет декомпозицию дерева, что означает фильтрацию с последующей понижающей дискретизацией (с коэффициентом 2 для двоичной схемы).

Обе функции waverec и upcoef могут привести к реконструкции.
Первый, waverec, выполняет прямую реконструкцию дерева, симметричную тому, что выполняется wavedec, что означает повышающую дискретизацию с последующей фильтрацией. На каждом уровне реконструкции (6 в вашем случае) также выполняется суммирование для получения сигнала с более подробной информацией, которая будет использоваться для следующего уровня реконструкции.
Вторая функция, upcoef, позволяет выполнять независимую реконструкцию данного подшкала без учета остальных деталей, содержащихся в других подшкалах. Обычно это выполняется заполнением нулями при восстановлении сигнала. Другими словами, upcoef можно рассматривать как оператор интерполяции.

В вашем случае вы использовали upcoef для интерполяции всех подшкал вейвлета из их децимированной x-grid в исходную x-grid. Затем вы выполнили суммирование всех интерполированных сигналов (содержащих только определенное и ограниченное количество деталей). Поскольку вейвлеты Добеши ортогональны, они приводят к идеальной реконструкции, и таким образом вы можете получить свой исходный сигнал после реконструкции.
Короче:

waverec        => direct reconstruction                        => original signal
n times upcoef => interpolation followed by a global summation => original signal

Интерполяция подшкалы полезна, только если вы хотите визуализировать все детали в одном и том же нерасеченном кадре x-grid. Такая интерполяция больше ничего не дает, так как количество информации, содержащейся в любой подшкале, и ее интерполированная версия одинаковы.