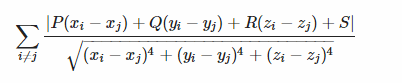Эффективный метод для свертки, как оценка суммы
Задача Даны N 3-мерных точек, которые являются {$p_1,p_2,..,p_n$}, где $p_i = (x_i,y_i,z_i) $ . Я должен найти значение формулы
для некоторых заданных постоянных целых чисел P, Q, R, S. все числа находятся в диапазоне от 1 до M ( = 100).
Мне нужен эффективный метод для расчета по этой формуле
Пожалуйста, дайте представление о том, как уменьшить сложность лучше, чем $O(n^2)$.
2 ответа
Предполагая, что все координаты находятся в диапазоне от 1 до 100, вы можете сделать это с помощью:
Вычислить 3d гистограмму всех точек O(100*100*100) операций.
Используйте БПФ для вычисления свертки гистограмм по каждой из 3 осей
Это приведет к трехмерной гистограмме трехмерных векторов. Затем вы можете перебрать эту гистограмму, чтобы вычислить желаемое значение.
Главное, что при вычислении свертки гистограммы значений вычисляется гистограмма парных разностей этих значений. Это также может быть использовано для вычисления гистограммы сумм значений аналогичным образом.
Ваша проблема выглядит как потенциальная проблема частиц (такая, как у вас, например, в электродинамике), где вы должны найти некоторый "потенциал" в этом месте (x_j, y_j) суммируя все элементарные вклады i-th частицы.
Быстрый алгоритм, характерный для этого класса задач, - это метод быстрого мультиполя. Посмотрите это ключевое слово, но я должен предупредить вас, что это ни в коем случае не просто понять или реализовать. Необходим сильный математический фон.