С реализация алгоритма разрешения потока с невзвешенными двунаправленными ребрами и узлами с пропускной способностью
Я попытался найти переполнение стека для ответа на мой вопрос. Я нашел эти ответы, но их решение не относится к моему делу, так как у меня есть ненаправленные края. Я не могу создать новую вершину с ребрами, идущими в Vin, и ребрами, идущими в Vout, так как нет "входящего" или "выходящего" в определенном направлении.
Алгоритм Эдмондса-Карпа для графа, который имеет узлы с пропускной способностью
(был второй вопрос стека, который я не могу найти, но это был тот же ответ)
Начальная проблема
Моя проблема в том, что у меня есть граф, где узлы имеют емкость, все ребра двунаправлены, и мне нужно найти все пути, которые позволят мне максимизировать поток N элементов через граф.
В основном это лемин с комнатами вместимостью 1 и двунаправленными ребрами бесконечной вместимости.
Представьте себе лабиринт, в котором в туннеле может находиться как можно больше людей, но только один человек на комнату. Они могут перемещаться из одной комнаты в другую за один ход. Как я могу сделать так, чтобы у меня были все возможности пройти от начала до конца лабиринта, не имея двух человек в одной комнате.
Реализация Эдмондс-Карп
Мне удалось реализовать Edmonds-Karp (вероятно, очень плохо), используя матрицу смежности (это 1-мерный массив целых чисел, использующий биты для проверки наличия соединения или нет).
У меня есть 3 функции, функция, которая запускает сам алгоритм (я немного упрощаю код, такой как удаление защиты для malloc, освобождения и т. Д., Чтобы алгоритм выглядел лучше):
- Основной алгоритм цикла
Это основной цикл. Я пытаюсь найти путь расширения. Если я этого не сделаю, это означает, что родительский номер (приемника) конечной комнаты будет равен начальному значению (-1). В противном случае я применяю путь, печатаю путь и продолжаю.
void edmonds_karp(t_map *map)
{
t_deque *deque;
uint32_t *flow;
int64_t *path;
t_way *way;
flow = ft_memalloc(sizeof(uint32_t) * map->size_rooms);
while (TRUE)
{
deque = ft_deque_create();
find_augmenting_path(deque, map, &flow, &path);
if (path[get_end_room(map)->id] == -1)
break ;
apply_augmenting_path(map, &flow, path);
way = build_way_from_path(path, map);
print_way(way);
ft_deque_delete(deque);
}
}
- Найти увеличивающий путь
Тогда есть функция, которая находит путь дополнения. Я просто использую BFS с очередью, выскакиваю родителя, а затем проверяю всех потомков. Если у потомка есть прямое соединение, но емкость остается, я добавляю его в путь, отмечаю как посещенный и помещаю в очередь. Если у потомка есть обратное соединение и поток проходит через него, я добавляю его в путь, отмечаю как посещенный и помещаю в очередь.
static int64_t find_augmenting_path(t_deque *deque, t_map *map, uint32_t **flow, int64_t **path)
{
uint32_t child_id;
uint8_t *visited;
t_room *parent;
t_room *child;
visited = ft_memalloc(sizeof(uint8_t) * map->size_rooms);
ft_deque_push_back(deque, get_start_room(map));
*path = init_path(map->size_rooms);
while (deque->head)
{
parent = ft_deque_pop_front(deque);
child_id = 0;
while (child_id < map->size_rooms)
{
if (!visited[child_id] && !map->rooms[child_id]->visited)
if ((((map->adj_matrix[parent->id] & (1ULL << child_id)) && !((*flow)[parent->id] & (1ULL << child_id))) // There is a forward connection and we still have capacity
|| ((map->adj_matrix[child_id] & (1ULL << parent->id)) && ((*flow)[child_id] & (1ULL << parent->id))))) // There is a backward connection and we have reverse capacity
{
child = get_room_by_id(map, child_id);
visited[child_id] = TRUE;
(*path)[child_id] = parent->id;
ft_deque_push_back(deque, (void*)child);
if (child->type == END)
return (SUCCESS);
}
++child_id;
}
}
return (ERROR);
}
- Применить добавочный путь
Функция, которая применяет путь дополнения, довольно проста, так как в моем случае емкость равна 1 для всех ребер. Мы просто возвращаемся с конца (раковина), пока не достигнем начала (касание), используя идентификаторы, сохраненные в пути. Для каждой комнаты мы заполняем емкость от родителя к ребенку и освобождаем емкость от ребенка к родителю.
static void apply_augmenting_path(t_map *map, uint32_t **flow, int64_t *path)
{
t_room *start;
t_room *parent;
t_room *child;
start = get_start_room(map);
child = get_end_room(map);
while (child->id != start->id)
{
parent = get_room_by_id(map, path[child->id]);
(*flow)[parent->id] |= 1ULL << child->id;
(*flow)[child->id] |= 0ULL << parent->id;
child = parent;
}
}
Есть проверка, которую я добавил в следующем состоянии:
if (!visited[child_id] && !map->rooms[child_id]->visited)
Эта проверка !map->rooms[child_id]->visited) это флаг посещения, который я добавляю, когда строю свой путь по найденному пути. Это позволяет мне избегать занимать одну и ту же комнату несколько раз в некоторых ситуациях.
Если у меня будет несколько ребер, в Эдмонде-Карпсе поток будет ограничен ребрами. Это означает, что если у меня есть 4 ребра к узлу, у меня может быть 2 элемента, если у меня есть 2 других ребра для элементов. Эти проверки позволяют избежать этой ситуации.
НО, и это моя главная проблема, делая это, я блокирую некоторые возможные пути через лабиринт.
Следующие фотографии покажут вам проблему. Без моей дополнительной проверки Эдмондс-Карп работает хорошо, но использует ребра, чтобы найти лучший поток:
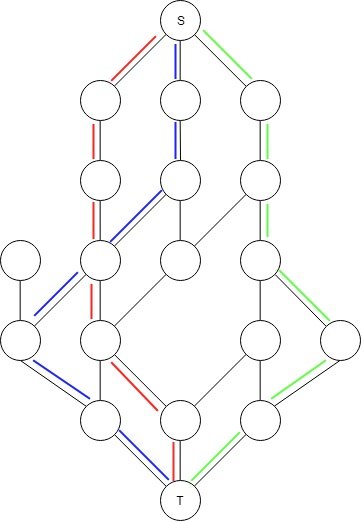
Вот решение, когда я добавляю свой чек, чтобы не использовать одну и ту же комнату дважды:
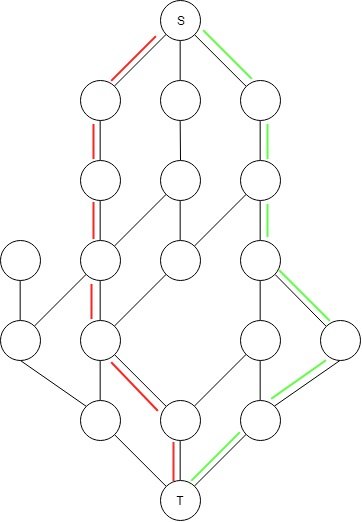
Вот что я хотел бы найти:
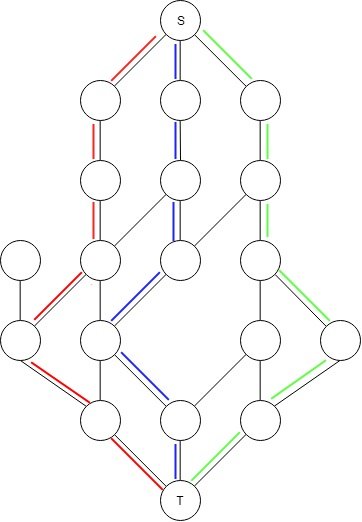
Есть ли способ изменить мою реализацию Edmonds-Karp, чтобы получить то, что я хочу? Если нет, есть ли другой алгоритм, который я мог бы использовать?
Спасибо всем большое за ваше терпение!
PS: я не могу вставлять картинки, потому что мне не хватает репутации:'(
1 ответ
Давайте начнем с чего-то простого, предполагая, что у нас есть простой граф с двумя узлами A и B, A, соединенными с B: A <-> B
Для каждого узла добавьте одну пару узлов, SA и EA для A, и SB и EB для B. (S означает начало и E означает конец)
- Из SA добавьте направленное ребро к узлу EA с емкостью, равной емкости узла A.
- Примените те же шаги с узлом B,
Теперь у нас есть график выглядит так:
SA -> EA
SB -> EB
Чтобы представить связь между A и B, мы добавляем направленное ребро из EA -> SB с неограниченной (очень большой) емкостью, аналогично, мы добавляем направленное ребро из EB -> SA
Итак, наш последний график:
SA -> EA
SB -> EB
EA -> SB
EB -> SA
Мы понимаем, что это преобразование может быть легко применено к более сложному графу, используя аналогичный процесс.
После применения преобразования теперь мы можем использовать стандартный алгоритм максимального потока для решения этой проблемы. Ура!