Инициализация неправильного смещения Tensorflow

Question

Я инициализирую свои 2 набора весов / смещений, используя ту же функцию

1-й сет:

W_omega = tf.Variable(tf.random_uniform([hidden_size, attention_size], -0.1, 0.1), name='W_omega')
b_omega = tf.Variable(tf.random_uniform([attention_size], -0.1, 0.1), name='b_omega')

2-й сет:

W = tf.Variable(tf.random_uniform([input_dim, output_dim], -0.1, 0.1), name='W_post_attn')  
b = tf.Variable(tf.random_uniform([output_dim], -0.1, 0.1), name='b_post_attn')

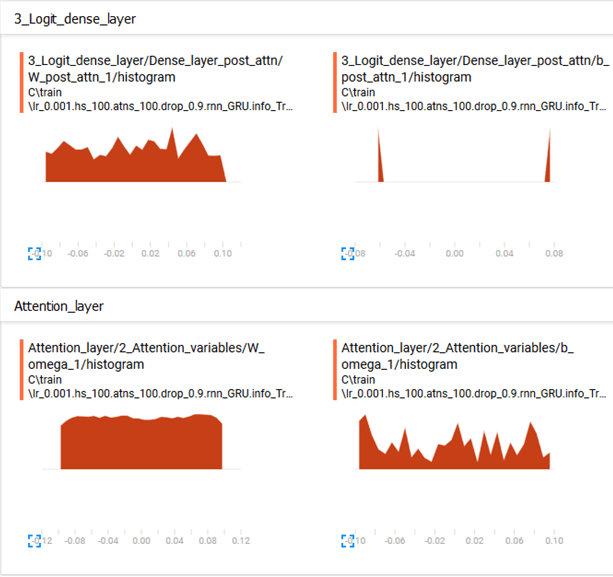
Но гистограмма в Tensorboard показывает, что 2-й набор смещения распределен неравномерно (двоичное распределение сосредоточено вокруг +/-0,06, см. Верхнее изображение ниже).

Есть идеи, что может быть причиной этого?

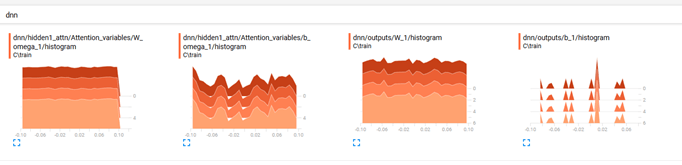
Добавление фиктивного кода с использованием данных MNIST и запуск на ноутбуке Jupyter. Обратите внимание, что мой оригинальный код является двоичной классификацией, в то время как MNIST имеет 10 классов. Кажется, что число пиков в выходном смещении (на последнем уровне) коррелирует с количеством выходных классов (см. Рисунок ниже).

from __future__ import division, print_function, unicode_literals
from functools import partial

import numpy as np
import os

import tensorflow as tf

def reset_graph(seed=42):
    tf.reset_default_graph()
    tf.set_random_seed(seed)
    np.random.seed(seed)

path = '/your_folder/'

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/mnist/tmp/data/")

reset_graph()

def variable_summaries(var, name):
  """Attach a lot of summaries to a Tensor (for TensorBoard visualization)."""
  with tf.name_scope(name):
    mean = tf.reduce_mean(var)
    tf.summary.scalar('mean', mean)
    tf.summary.scalar('max', tf.reduce_max(var))
    tf.summary.scalar('min', tf.reduce_min(var))
    tf.summary.histogram('histogram', var)

n_inputs = 28*28  # MNIST
n_hidden1 = 200
n_outputs = 10

learning_rate = 0.01

n_epochs = 50
batch_size = 50

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")

def attention(inputs, attention_size, name):
    hidden_size = int(inputs.get_shape()[1])

    # Trainable parameters
    with tf.name_scope(name):
        with tf.name_scope('Attention_variables'):
            W_omega = tf.Variable(tf.random_uniform([hidden_size, attention_size], -0.1, 0.1), name='W_omega')
            b_omega = tf.Variable(tf.random_uniform([attention_size], -0.1, 0.1), name='b_omega')
            u_omega = tf.Variable(tf.random_uniform([attention_size], -0.1, 0.1), name='u_omega')

            variable_summaries(W_omega, 'W_omega')
            variable_summaries(b_omega, 'b_omega')

        with tf.name_scope('Attention_u_it'):
            v = tf.tanh(tf.tensordot(inputs, W_omega, axes=[[1], [0]]) + b_omega, name='u_it')

        with tf.name_scope('Attention_alpha_it'):
            vu = tf.tensordot(v, u_omega, axes=[[1], [0]], name='u_it_u_w')   
            alphas = tf.nn.softmax(vu, name='alphas')              

        with tf.name_scope('Attention_output'):
            #output = tf.reduce_sum(inputs * tf.expand_dims(alphas, -1), 1, name='attention_output')
            output = inputs * tf.expand_dims(alphas, -1)
    return output


def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int(X.get_shape()[1])
        W = tf.Variable(tf.random_uniform([n_inputs, n_neurons], -0.1, 0.1), name='W')
        b = tf.Variable(tf.random_uniform([n_neurons], -0.1, 0.1), name='b')

        variable_summaries(W, 'W')
        variable_summaries(b, 'b')
        if activation is not None:
            return activation(tf.matmul(X, W) + b)
        else:
            return tf.matmul(X, W) + b


with tf.name_scope("dnn"):
    hidden1 = attention(X, n_hidden1, name="hidden1_attn")
    logits = neuron_layer(hidden1, n_outputs, name="outputs")

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
                                                              logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

with tf.name_scope("train"):
    opt = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = opt.minimize(loss)

with tf.name_scope("eval"):
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
saver = tf.train.Saver()

#tensorboard saving parameters
from datetime import datetime
now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "/tensorboard_files/"
logdir = "{}/run-{}/".format(root_logdir, now)

# Merge all the summaries and write them out to /tmp/mnist_logs (by default)
merged = tf.summary.merge_all()
train_writer = tf.summary.FileWriter(logdir+'/train', tf.get_default_graph())


with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
        if epoch%2==0:    
            acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})        
            #tensorboard summary
            summary = sess.run(merged, feed_dict={X: X_batch, y: y_batch})
            train_writer.add_summary(summary, epoch)

            acc_val = accuracy.eval(feed_dict={X: mnist.validation.images,
                                                y: mnist.validation.labels})
            print(epoch, "Train accuracy:", acc_train, "Val accuracy:", acc_val)

    save_path = saver.save(sess, path+"my_model_final.ckpt")

Answer 1

Значение ключа, которое определяет, как выглядит гистограмма, является размером случайного вектора, в вашем случае это attention_size=200 а также n_neurons=10 (или же output_dim=2 в первом фрагменте). Ясно, что чем больше размер выборки, тем ближе образец к однородному. Вот почему распределение b_omega больше похоже на форму, чем на распределение b,

Задавать attention_size=10 и вот что вы увидите: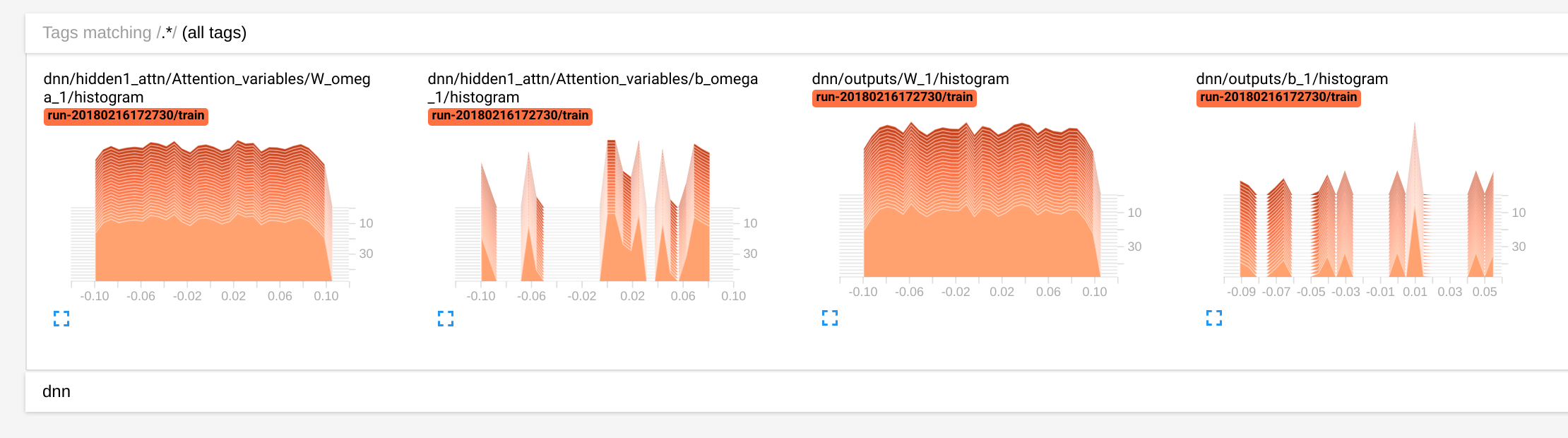

Настоящий b значения за этим графиком (обратите внимание на пики в 0.01):

[ 0.05595738  0.01231904 -0.08605836  0.01057353 -0.03015073 -0.04255719
  0.04719915  0.01116617 -0.0672287  -0.00013051]

Настоящий b_omega значения:

[-0.06326838 -0.09758444  0.06982093  0.01574633  0.0039237   0.07463291
  0.02308519  0.04594345  0.07912541  0.00175323]

Также обратите внимание, что распределения были одинаковыми в каждую эпоху (это глубина диаграммы), потому что никакие веса и смещения никогда не обновляются.

Итог: инициализация верна, но гистограмма может сбивать с толку, если не обращать внимания на форму переменных.