Как работает минимизация DFA?
Что-то не так с этими заметками, написанными моим профессором?
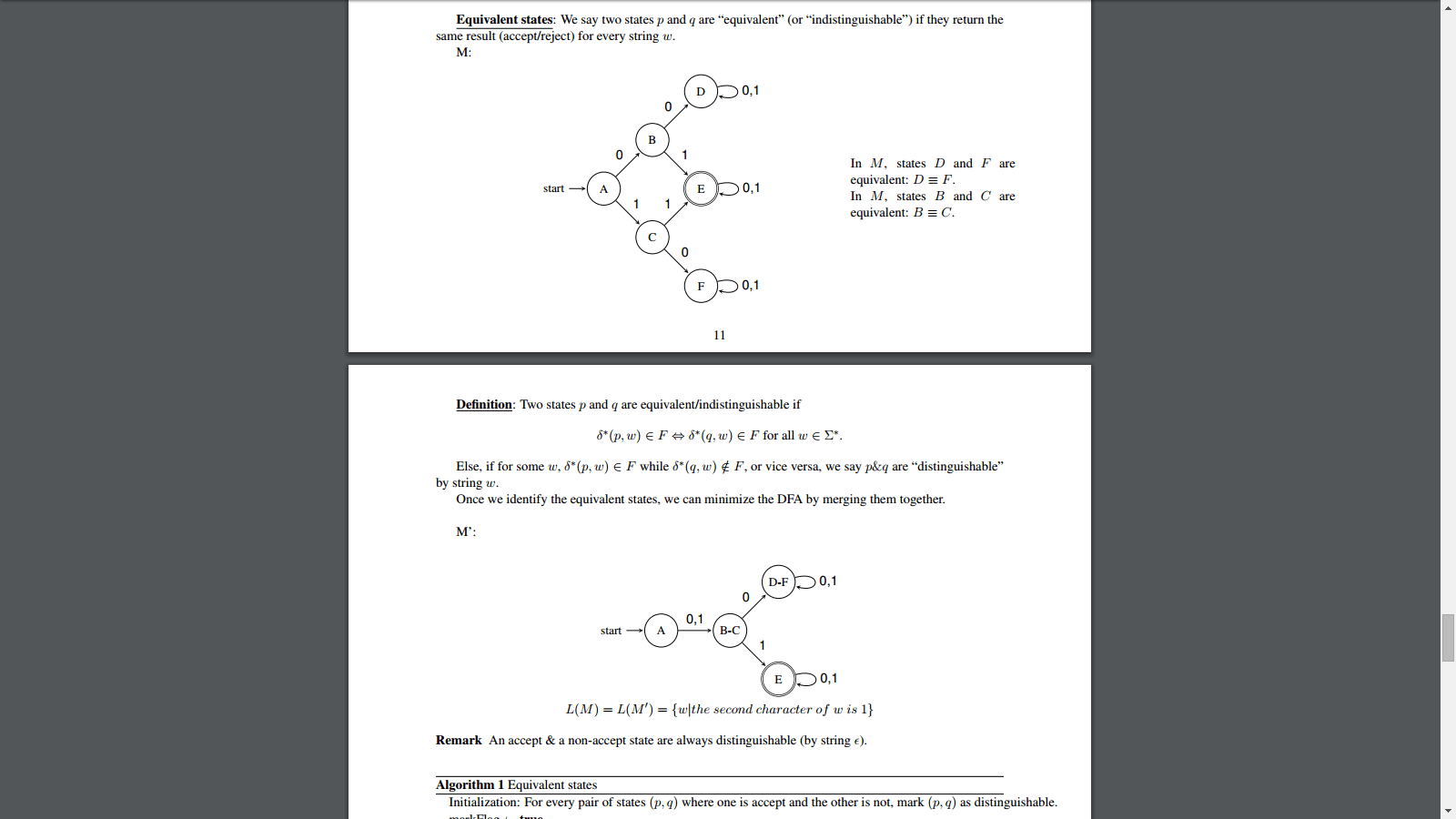
Насколько D&F и B&C эквивалентны?
Они не должны быть, потому что функции транзакций дают разные состояния. Если это нормально, и мы заботимся об эквивалентности одного и того же ввода, принятого или отклоненного в обоих состояниях, то почему D и B не эквивалентны?
Дополнительный вопрос:
В чем разница между транзакцией и звездочкой транзакции, если вы знакомы с обозначениями?
В чем разница между обозначением суммы и звездой суммы?
Замечание внизу гласит: "... по эпсилону". Что это значит? Я не использовал эпсилон.
Любая помощь приветствуется. Спасибо!
1 ответ
Я не знаю, что вы подразумеваете под "транзакцией" или "звездой транзакции", но, посмотрев на "нотацию суммы" и "звезду суммы", я подозреваю, что вы имеете в виду одну из греческих букв.
Итак, сначала давайте разберемся с этим немного путаницы.
Этот символ здесь не называется "сумма": Σ
Это буква в греческом алфавите, называемая "сигма". Как и латинский алфавит, греческие буквы имеют заглавные и строчные буквы. Этот символ - заглавная сигма.
Этот символ очень часто используется для обозначения суммы. Тем не менее, есть определенные разделы математики, где традиционно использование заглавной сигмы означает нечто иное. По сути, рассматривайте это как очередное письмо, хотя и немного странное.
Теперь, потому что вы изучаете теорию языка, есть некоторые традиционные вещи, которые обозначают различные буквы. Это, вероятно, в вашем тексте или в другом месте ранее в заметках вашего профессора, но на самом деле это не более загадочно, чем соглашение о том, что "х" часто представляет, как далеко влево или вправо поставить точку, а "у" часто представляет, насколько высоко или вниз, чтобы поставить точку.
В частности, в теории языка информатики традиционно используется Σ для обозначения "алфавита" (как, например, набор символов).
Кроме того, в теории языка, если у вас есть набор чего-либо, традиционно использовать этот набор, за которым следует верхняя звездочка, означающая "строки, составленные из элементов этого набора". Так, например, если я скажу:
Пусть S = {0, 1}. Напишите пять примеров элементов S *
тогда один адекватный ответ будет:
ϵ "1" "111000" "0101" "110011001100111"
Обратите внимание, что я использовал ϵ там! В теории языка ϵ означает пустую строку.
Из контекста, похоже, что нотация в вашем классе - использовать строчную дельту (δ) для обозначения функции перехода DFA. Например, на первом слайде δ(B,0) = D и δ(B,1) = E. Кроме того, похоже, что они используют (δ) для обозначения функции, которая принимает начальное состояние и строку и говорит, куда эта строка берет вещи. Итак, на первой диаграмме δ (A, "11") = E.
Теперь давайте вернемся и объясним каждый из этих заметок.
Во-первых, на первом слайде слайд начинается с того, что два состояния эквивалентны, если и только если они принимают одинаковые строки, начиная с этих состояний. Теперь давайте посмотрим, какие строки принимаются начиная с B и C: любая строка, начинающаяся с "1", переходит в E и принимается (поскольку после E все пути снова возвращаются в E); любая строка, начинающаяся с "0", попадает в D или F, где она находится, и отклоняется.
Вы спрашиваете, почему B и D не эквивалентны - рассмотрите строку "1", с одним символом. Если вы начинаете с B, эта строка принимается. (Потому что он переходит к E, состояние принятия). Если вы начинаете с D, эта строка отклоняется (потому что D, где она заканчивается, не является состоянием принятия).
Теперь определение в верхней части второго этапа просто помещает понятие о том, имеют ли строки разные результаты, начиная с разных состояний, в формальный язык. Это говорит о том, что два состояния эквивалентны, если они оказываются в принимающем состоянии после следующей строки w, то же самое для обоих состояний, для всех строк w. В противном случае есть некоторая строка w, такая, что из одного состояния вы переходите в состояние принятия при продолжении работы с w, а из другого состояния вы попадаете в непринятое состояние. Затем вы говорите, что состояния "различимы" этой строкой w.
В примечании внизу, о котором вы спрашивали, просто отмечается, что принимающее состояние и неприемлемое состояние всегда различаются по пустой строке (помните, что в теории языка это означает ϵ). Это имеет смысл, поскольку δ * (A, ϵ) = A для всех состояний A и всех DFA (после пустой строки никуда не денется).