Интерполяция через заполнение пространства Фурье

Question

Недавно я попытался реализовать на matlab простой пример метода интерполяции с использованием заполнения нулями в области Фурье. Но я не могу получить эту работу должным образом, у меня всегда небольшой сдвиг частоты, едва заметный в пространстве Фурье, но он генерирует огромную ошибку во временном пространстве.

Поскольку заполнение нулями в пространстве Фурье, кажется, является распространенным (и быстрым) методом интерполяции, я предполагаю, что мне чего-то не хватает:

Вот код Matlab:

clc;
clear all;
close all;


Fe = 3250;
Te = 1/Fe;
Nech = 100;

F1 = 500;
F2 = 1000;
FMax = 1500;

time = [0:Te:(Nech-1)*Te];
timeDiscrete = [1:1:Nech];
frequency = (timeDiscrete/Nech)*Fe;

signal = cos(2*pi*F1*(time))+cos(2*pi*F2*(time))+cos(2*pi*FMax*(time));

%Compute the FFT
spectrum=zeros(1,Nech);
for k = timeDiscrete
    for l = timeDiscrete
        spectrum(k) = spectrum(k) + signal(l)*exp(-2*pi*j*l*k/Nech);
    end
end

%Compute de inverse FFT
reconstruction=zeros(1,Nech);
for k = timeDiscrete
    for l = timeDiscrete
        reconstruction(k) = reconstruction(k) + spectrum(l)*exp(2*pi*j*l*k/Nech);
    end
end
reconstruction=reconstruction/Nech;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%    Now interpolation will take place   %%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Finterp = 6*Fe;
Tinterp = 1/Finterp;
TimeInterp = [0:Tinterp:(Nech-1)*Te];
[m,n] = size(TimeInterp);
NechInterp = n;
TimeInterpDiscrete = [1:1:NechInterp];

%Compute original signal value without any interpolation
signalResampled = cos(2*pi*F1*(TimeInterp))+cos(2*pi*F2*(TimeInterp))+cos(2*pi*FMax*(TimeInterp));

%Compute original signal interpolation by padding the fft and performing
%inverse fft on the result
semipaddedsize=floor(NechInterp/2);
padded_spectrum0 = zeros(1,semipaddedsize);
padded_spectrum0 = padarray(spectrum(1:Nech/2),[0 semipaddedsize-(Nech/2)],0,'post');
padded_spectrum = zeros(1,NechInterp);
padded_spectrum(1:semipaddedsize) = padded_spectrum0;
padded_spectrum(semipaddedsize+1:NechInterp-1) = conj(fliplr(padded_spectrum0));
% padded_spectrum = padarray(spectrum,[0 NechInterp-Nech],0,'post');
padded_timeDiscrete = [1:1:NechInterp];
padded_reconstruction = zeros(1,NechInterp);


for k = padded_timeDiscrete
    for l = padded_timeDiscrete
        padded_reconstruction(k) = padded_reconstruction(k) + padded_spectrum(l)*exp(2*pi*j*l*k/NechInterp);
    end
end
padded_reconstruction=padded_reconstruction/(1*Nech);


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%       Let's print out the result       %%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

spectrumresampled=zeros(1,NechInterp);
for k = TimeInterpDiscrete
    for l = TimeInterpDiscrete
        spectrumresampled(k) = spectrumresampled(k) + signalResampled(l)*exp(-2*pi*j*l*k/NechInterp);
    end
end

figure(2);
plot(abs(spectrumresampled)/6,'g');
hold on;
plot(abs(padded_spectrum),'b');

figure(3);

% Ground truth : deterministic signal is recomputed
plot(TimeInterp,signalResampled,'g');
hold on;
% linear interpolation between subsampled points (matlab tracing tool)
plot(time,(reconstruction),'c');
hold on;
% Padding the spectrum and reconstructing it 
plot(TimeInterp,real(padded_reconstruction),'m');
hold on;

xlabel('Time in s','FontSize',16)
ylabel('Signal value (no unit)','FontSize',16)
title('\it{ Various signal reconstruction from fourier transform }','FontSize',16)
legend('True signal', 'Reconstruction with linear interpolation', 'Reconstruction with padded spectrum');

Я не могу публиковать изображения результатов из-за моей репутации, но график легко генерируется с помощью Matlab. Я был бы очень признателен за комментарий к этому коду или к полям с нулевым отступом для интерполяции в целом.

заранее спасибо

Answer 1

Большое спасибо вам обоим за эти советы, я решил ответить на свой вопрос, потому что в поле для комментариев было недостаточно места:

@ Попробуй, я действительно определил неправильный дискретный вектор времени, как @Frederick также указал, что у меня была проблема с заполнением моего вектора, спасибо, что дал мне правильный "способ Matlab" сделать это, я не должен был так бояться из fftshift/ifftshift, кроме того, использование padarray с 'both' также сделало бы эту работу, как упомянуто @Frederick .

Свертывание цикла for также было важным шагом для правильной реализации matlab, который я не использую в обучающих целях, чтобы облегчить мое понимание и связанную проверку.

Еще один очень интересный момент @Try, упомянутый в первом предложении, и то, что я не осознал в первую очередь, заключается в том факте, что заполнение нулями является просто эквивалентом свертывания моих данных во временной области функцией sinc.

На самом деле, я думаю, что это буквально эквивалентно свертке с псевдонимной функцией sinc, также называемой ядром дирихле, которая ограничивает при увеличении частоты дискретизации до бесконечности классическую функцию sinc (см. http://www.dsprelated.com/dspbooks/sasp/Rectangular_Window_I.html)

Я не разместил здесь весь код, но цель моей исходной программы состояла в том, чтобы сравнить формулу свертки ядра Дирихле, которую я продемонстрировал в другом контексте (теоретическая демонстрация с использованием дискретного выражения ряда Фурье), формулу интерполяции Уинтекера – Шеннона и свертку sinc, и заполнение нулями, поэтому мне нужно дать очень похожий результат.

На вопрос об аподизации, я думаю, что истинный ответ таков: если ваш сигнал ограничен по полосе, вам не нужна другая функция аподизации, кроме прямоугольного окна.

Если ваш сигнал не ограничен по полосе частот или не имеет псевдонимов относительно частоты дискретизации, вам нужно будет уменьшить вклад псевдонимной части спектра, что достигается путем их фильтрации с помощью окна частотного фильтра = аподирования в частотной области, которое превращается в конкретные интерполяционные ядра во временной области.

Answer 2

Результат, который вы наблюдаете во временной области, звонит из-за свертывания функции sinc с вашими исходными данными. Это эквивалентно во временной области умножения на прямоугольное окно в частотной области, которое фактически является тем, что вы делаете, когда заполняете ноль. Не забудьте извиниться!

Я публикую ваш код после свертывания циклов (что значительно ускоряет вычисления), переопределения диапазонов временных и частотных переменных (см. Определение DFT, чтобы понять почему) и удаления одной из выполняемых вами операций заполнения, которые я, честно говоря, не делал понять суть.

clc;
clear all;
close all;

Fe = 3250;
Te = 1/Fe;
Nech = 100;
mlt = 10;
F1 = 50; 
F2 = 100; 
FMax = 150; 

time = [0:Te:(Nech-1)*Te];
%timeDiscrete = [1:1:Nech];
timeDiscrete = [0:1:Nech-1];
frequency = (timeDiscrete/Nech)*Fe;

signal = cos(2*pi*F1*(time))+cos(2*pi*F2*(time))+cos(2*pi*FMax*(time));
spectrum =  signal*exp(-2*pi*j*timeDiscrete'*timeDiscrete/Nech);
fspec = [0:Nech-1]*Fe/Nech;
reconstruction = spectrum*exp(2*pi*j*timeDiscrete'*timeDiscrete/Nech)/Nech;

figure
plot(time,signal)
hold on
plot(time,reconstruction,'g:')

% **** interpolation ****

Finterp = 6*Fe;
Tinterp = 1/Finterp;
TimeInterp = [0:Tinterp:(Nech-1)*Te];
NechInterp = length(TimeInterp);
%TimeInterpDiscrete = [1:NechInterp];
TimeInterpDiscrete = [0:NechInterp-1];

%Compute original signal value without any interpolation
signalResampled = cos(2*pi*F1*(TimeInterp))+cos(2*pi*F2*(TimeInterp))+cos(2*pi*FMax*(TimeInterp));

%Compute original signal interpolation by padding the fft and performing
%inverse fft on the result
padded_spectrum0 = spectrum;
padded_spectrum0(NechInterp) = 0;
fspecPadded = [0:NechInterp-1]*Finterp/NechInterp;

padded_reconstruction = padded_spectrum0*exp(2*pi*j*TimeInterpDiscrete'*TimeInterpDiscrete/NechInterp)/(1*Nech);
spectrumresampled = signalResampled*exp(-2*pi*j*TimeInterpDiscrete'*TimeInterpDiscrete/NechInterp);
fresampled = [0:NechInterp-1]*Fe/NechInterp;

% **** print out ****

figure(2);
hold on;
plot(fspec,abs(spectrum),'c');
plot(fresampled,abs(spectrumresampled)/6,'g--');
plot(fspecPadded,abs(padded_spectrum0),'m:');
xlabel('Frequency in Hz','FontSize',16)
ylabel('Signal value (no unit)','FontSize',16)
legend('True signal', 'Reconstruction with resampled spectrum', 'Padded spectrum');

figure(3);
% Ground truth : deterministic signal is recomputed
plot(TimeInterp,signalResampled,'g');
hold on;
% Padding the spectrum and reconstructing it 
plot(TimeInterp,real(padded_reconstruction),'m:');
xlabel('Time in s','FontSize',16)
ylabel('Signal value (no unit)','FontSize',16)
title('\it{ Various signal reconstruction from fourier transform }','FontSize',16)
legend('True signal', 'Reconstruction with padded spectrum');

А вот изображение ужасно искаженного сигнала из-за заполнения в частотной области:

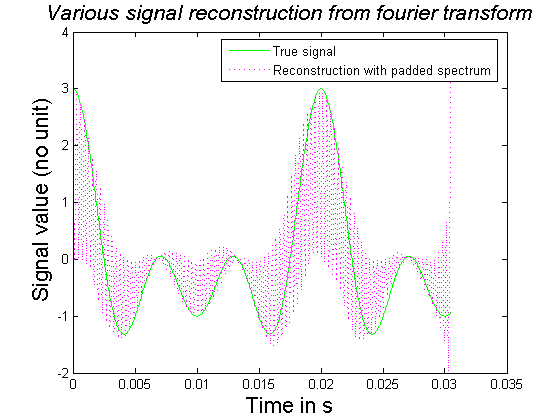
Некоторое улучшение возможно при первом применении fftshift для центрирования спектра и заполнения на чередующихся сторонах центрированного спектра, затем инвертируя fftshift операция:

Nz = NechInterp-Nech;
padded_spectrum0 = ifftshift([ zeros(1,floor(Nz/2)) fftshift(spectrum) zeros(1,floor(Nz/2)+rem(Nz,2)) ]); % replaces (NechInterp) = 0;
fspecPadded = [0:NechInterp-1]*Finterp/NechInterp;

Затем вы получите гораздо более приятный интерполированный сигнал во временной области, потому что операция заполнения не приводит к таким резким спадам в спектре (однако некоторые улучшения могут все же быть возможными при дальнейшем использовании):

Answer 3

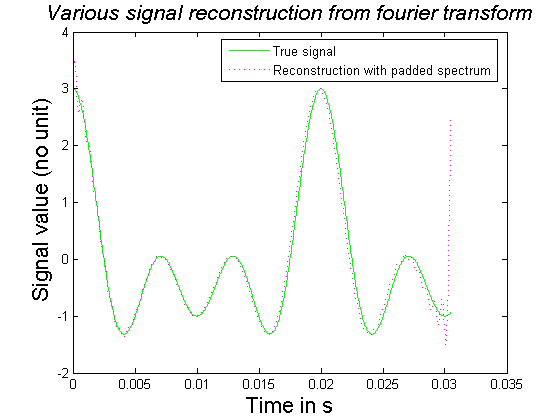
ХОРОШО. Одной из проблем было то, как вы делали IDFT для padded_reconstruction. То, как вы определили TimeInterp и, следовательно, NechInterp, сделало элементы комплексного показателя неправильными. Это объясняет неправильные частоты.

Затем возникла проблема с включением средней точки в область Фурье (pt 50) дважды. Он был близок к нулю, поэтому он не создавал чрезвычайно очевидной проблемы, но он должен быть включен только один раз. Я переписал этот раздел, потому что мне было трудно проработать его так, как вы это сделали. Я держал это очень близко все же. Если бы я делал это, я использовал бы fftshift, а затем padarray(...,'both'), что избавило бы от необходимости помещать нули в середину. Если вы делаете это для обучения и стараетесь не использовать инструменты Matlab (например, fftshift), тогда не берите в голову.

Я также переделал то, как вы определяете время, но, если честно, я думаю, это может сработать по-вашему.

Я указал изменения с%<<<<<<<<<<

Fe = 3250;
Te = 1/Fe;
Nech = 100;

F1 = 500;
F2 = 1000;
FMax = 1500;

time = [Te:Te:(Nech)*Te];  %<<<<<<<<<<
timeDiscrete = [1:1:Nech];
frequency = (timeDiscrete/Nech)*Fe;

signal = cos(2*pi*F1*(time))+cos(2*pi*F2*(time))+cos(2*pi*FMax*(time));

%Compute the FFT
spectrum=zeros(1,Nech);
for k = timeDiscrete
    for l = timeDiscrete
        spectrum(k) = spectrum(k) + signal(l)*exp(-2*pi*j*l*k/Nech);
    end
end

%Compute de inverse FFT
reconstruction=zeros(1,Nech);
for k = timeDiscrete
    for l = timeDiscrete
        reconstruction(k) = reconstruction(k) + spectrum(l)*exp(2*pi*j*l*k/Nech);
    end
end
reconstruction=reconstruction/Nech;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%    Now interpolation will take place   %%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Finterp = 6*Fe;
Tinterp = 1/Finterp;
TimeInterp = [Tinterp:Tinterp:(Nech*6)*Tinterp];  %<<<<<<<<<<
[m,n] = size(TimeInterp);
NechInterp = n;
TimeInterpDiscrete = [1:1:NechInterp];

%Compute original signal value without any interpolation
signalResampled = cos(2*pi*F1*(TimeInterp))+cos(2*pi*F2*(TimeInterp))+cos(2*pi*FMax*(TimeInterp));

%Compute original signal interpolation by padding the fft and performing
%inverse fft on the result
padded_spectrum = zeros(1,NechInterp); %<<<<<<<<<<
padded_spectrum(1:floor(Nech/2-1)) = spectrum(1:floor(Nech/2-1)); %<<<<<<<<<<
padded_spectrum(end-floor(Nech/2)+1:end) = spectrum(floor(Nech/2)+1:end); %<<<<<<<<<<

padded_reconstruction = zeros(1,NechInterp);
for k = TimeInterpDiscrete %<<<<<<<<<<(no reason for new variable)
    for l = TimeInterpDiscrete %<<<<<<<<<<(no reason for new variable)
        padded_reconstruction(k) = padded_reconstruction(k) + padded_spectrum(l)*exp(2*pi*j*l*k/NechInterp);
    end
end
padded_reconstruction=padded_reconstruction/(1*Nech);