Объедините geom_tile() и facet_grid/facet_wrap и удалите пробел между плитками (ggplot2)

Question

У меня есть набор данных с х, у и г (resp) значения вместе с двумя столбцами для фасетирования, чтобы создать сетку плиточных графиков.

Выход из dput() находится в конце поста.

library(ggplot2)

Мой фактический набор данных имеет шесть уникальных взаимодействий между переменными, однако я ограничил его четырьмя для простоты. Я могу создать плитку с каждой уникальной комбинацией, но не со всем набором. Выход из dput() находится в конце поста. Я думал, что это может быть связано с ggplot нужен общий масштаб по оси Y, но это не проблема.

library(ggplot2)
p <- ggplot(data_sub, aes(x = x, y = y)) + geom_tile(aes(fill = resp))
p <- p + facet_wrap(var2 ~ var1, scales = "free", ncol = 2)

Выход:

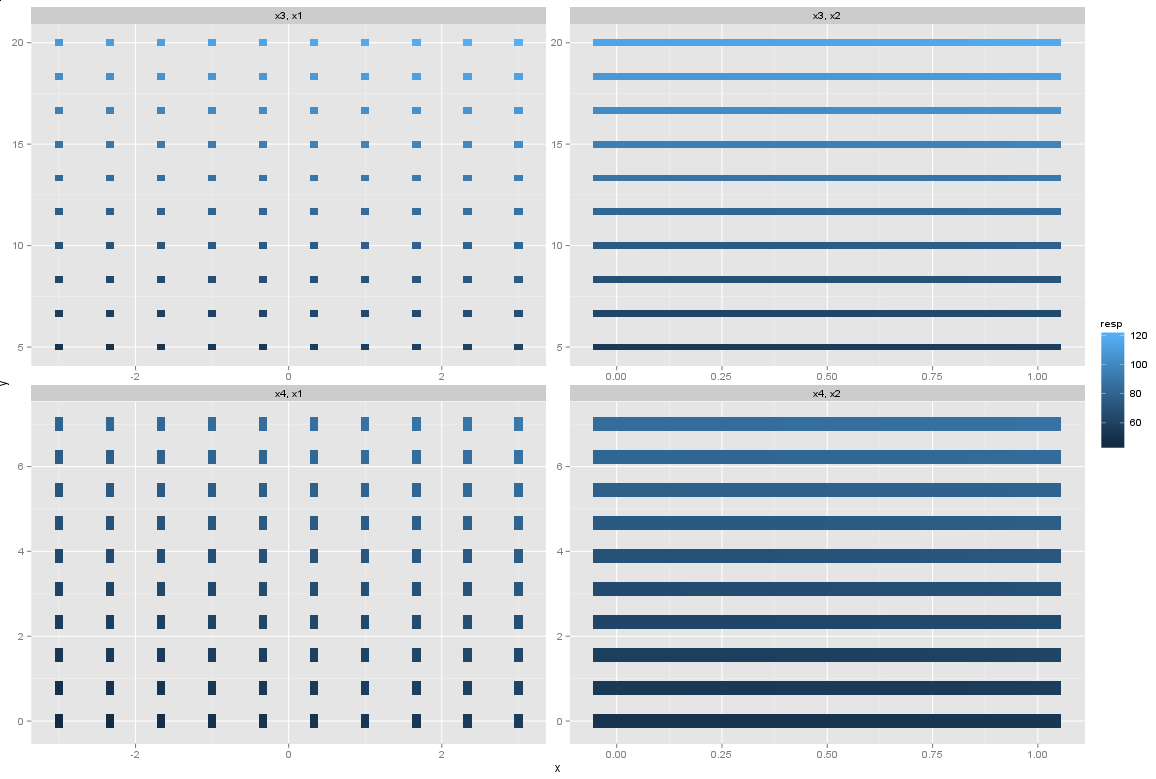
Сюжет сделан самостоятельно, таких пробелов нет:

x1x2 <- data_sub[data_sub$var1 == "x1" & data_sub$var2 == "x3", ]
ggplot(x1x2, aes(x = x, y = y)) + geom_tile(aes(fill = resp))

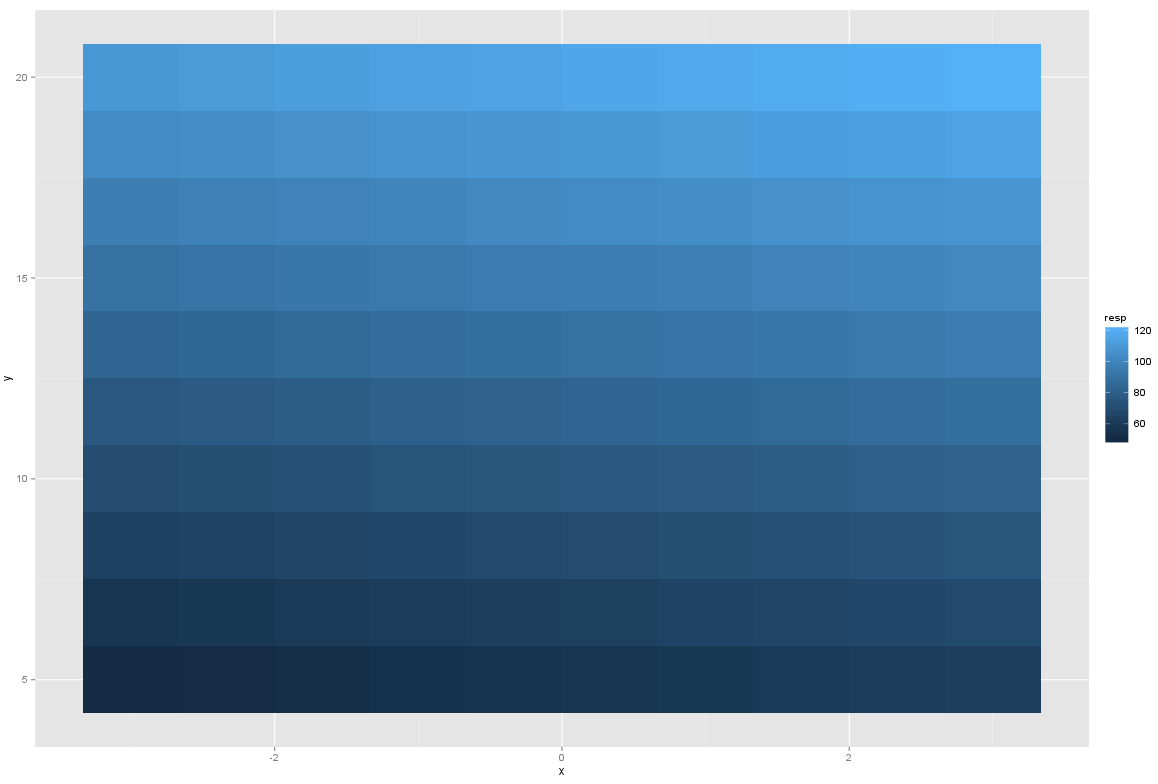
Я считаю, что проблема определяет какую-то динамику height а также width эстетическое в geom_tile() позвони, но я не уверен, как это сделать. Похоже, что на одном тайле будет использоваться что-то вроде diff((unique(x)) придумать подходящую высоту, но я не уверен, как это сделать для каждого уровня фасета - это единственный способ создать такие столбцы в моем фрейме данных?

---

Данные:

dput(data_sub)
structure(list(x = c(-3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, -3, -2.33333333333333, -1.66666666666667, 
-1, -0.333333333333333, 0.333333333333333, 1, 1.66666666666667, 
2.33333333333333, 3, 0, 0.111111111111111, 0.222222222222222, 
0.333333333333333, 0.444444444444444, 0.555555555555556, 0.666666666666667, 
0.777777777777778, 0.888888888888889, 1, 0, 0.111111111111111, 
0.222222222222222, 0.333333333333333, 0.444444444444444, 0.555555555555556, 
0.666666666666667, 0.777777777777778, 0.888888888888889, 1, 0, 
0.111111111111111, 0.222222222222222, 0.333333333333333, 0.444444444444444, 
0.555555555555556, 0.666666666666667, 0.777777777777778, 0.888888888888889, 
1, 0, 0.111111111111111, 0.222222222222222, 0.333333333333333, 
0.444444444444444, 0.555555555555556, 0.666666666666667, 0.777777777777778, 
0.888888888888889, 1, 0, 0.111111111111111, 0.222222222222222, 
0.333333333333333, 0.444444444444444, 0.555555555555556, 0.666666666666667, 
0.777777777777778, 0.888888888888889, 1, 0, 0.111111111111111, 
0.222222222222222, 0.333333333333333, 0.444444444444444, 0.555555555555556, 
0.666666666666667, 0.777777777777778, 0.888888888888889, 1, 0, 
0.111111111111111, 0.222222222222222, 0.333333333333333, 0.444444444444444, 
0.555555555555556, 0.666666666666667, 0.777777777777778, 0.888888888888889, 
1, 0, 0.111111111111111, 0.222222222222222, 0.333333333333333, 
0.444444444444444, 0.555555555555556, 0.666666666666667, 0.777777777777778, 
0.888888888888889, 1, 0, 0.111111111111111, 0.222222222222222, 
0.333333333333333, 0.444444444444444, 0.555555555555556, 0.666666666666667, 
0.777777777777778, 0.888888888888889, 1, 0, 0.111111111111111, 
0.222222222222222, 0.333333333333333, 0.444444444444444, 0.555555555555556, 
0.666666666666667, 0.777777777777778, 0.888888888888889, 1, 0, 
0.111111111111111, 0.222222222222222, 0.333333333333333, 0.444444444444444, 
0.555555555555556, 0.666666666666667, 0.777777777777778, 0.888888888888889, 
1, 0, 0.111111111111111, 0.222222222222222, 0.333333333333333, 
0.444444444444444, 0.555555555555556, 0.666666666666667, 0.777777777777778, 
0.888888888888889, 1, 0, 0.111111111111111, 0.222222222222222, 
0.333333333333333, 0.444444444444444, 0.555555555555556, 0.666666666666667, 
0.777777777777778, 0.888888888888889, 1, 0, 0.111111111111111, 
0.222222222222222, 0.333333333333333, 0.444444444444444, 0.555555555555556, 
0.666666666666667, 0.777777777777778, 0.888888888888889, 1, 0, 
0.111111111111111, 0.222222222222222, 0.333333333333333, 0.444444444444444, 
0.555555555555556, 0.666666666666667, 0.777777777777778, 0.888888888888889, 
1, 0, 0.111111111111111, 0.222222222222222, 0.333333333333333, 
0.444444444444444, 0.555555555555556, 0.666666666666667, 0.777777777777778, 
0.888888888888889, 1, 0, 0.111111111111111, 0.222222222222222, 
0.333333333333333, 0.444444444444444, 0.555555555555556, 0.666666666666667, 
0.777777777777778, 0.888888888888889, 1, 0, 0.111111111111111, 
0.222222222222222, 0.333333333333333, 0.444444444444444, 0.555555555555556, 
0.666666666666667, 0.777777777777778, 0.888888888888889, 1, 0, 
0.111111111111111, 0.222222222222222, 0.333333333333333, 0.444444444444444, 
0.555555555555556, 0.666666666666667, 0.777777777777778, 0.888888888888889, 
1, 0, 0.111111111111111, 0.222222222222222, 0.333333333333333, 
0.444444444444444, 0.555555555555556, 0.666666666666667, 0.777777777777778, 
0.888888888888889, 1), y = c(5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6.66666666666667, 
6.66666666666667, 6.66666666666667, 6.66666666666667, 6.66666666666667, 
6.66666666666667, 6.66666666666667, 6.66666666666667, 6.66666666666667, 
6.66666666666667, 8.33333333333333, 8.33333333333333, 8.33333333333333, 
8.33333333333333, 8.33333333333333, 8.33333333333333, 8.33333333333333, 
8.33333333333333, 8.33333333333333, 8.33333333333333, 10, 10, 
10, 10, 10, 10, 10, 10, 10, 10, 11.6666666666667, 11.6666666666667, 
11.6666666666667, 11.6666666666667, 11.6666666666667, 11.6666666666667, 
11.6666666666667, 11.6666666666667, 11.6666666666667, 11.6666666666667, 
13.3333333333333, 13.3333333333333, 13.3333333333333, 13.3333333333333, 
13.3333333333333, 13.3333333333333, 13.3333333333333, 13.3333333333333, 
13.3333333333333, 13.3333333333333, 15, 15, 15, 15, 15, 15, 15, 
15, 15, 15, 16.6666666666667, 16.6666666666667, 16.6666666666667, 
16.6666666666667, 16.6666666666667, 16.6666666666667, 16.6666666666667, 
16.6666666666667, 16.6666666666667, 16.6666666666667, 18.3333333333333, 
18.3333333333333, 18.3333333333333, 18.3333333333333, 18.3333333333333, 
18.3333333333333, 18.3333333333333, 18.3333333333333, 18.3333333333333, 
18.3333333333333, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 0, 
0, 0, 0, 0, 0, 0, 0, 0, 0, 0.777777777777778, 0.777777777777778, 
0.777777777777778, 0.777777777777778, 0.777777777777778, 0.777777777777778, 
0.777777777777778, 0.777777777777778, 0.777777777777778, 0.777777777777778, 
1.55555555555556, 1.55555555555556, 1.55555555555556, 1.55555555555556, 
1.55555555555556, 1.55555555555556, 1.55555555555556, 1.55555555555556, 
1.55555555555556, 1.55555555555556, 2.33333333333333, 2.33333333333333, 
2.33333333333333, 2.33333333333333, 2.33333333333333, 2.33333333333333, 
2.33333333333333, 2.33333333333333, 2.33333333333333, 2.33333333333333, 
3.11111111111111, 3.11111111111111, 3.11111111111111, 3.11111111111111, 
3.11111111111111, 3.11111111111111, 3.11111111111111, 3.11111111111111, 
3.11111111111111, 3.11111111111111, 3.88888888888889, 3.88888888888889, 
3.88888888888889, 3.88888888888889, 3.88888888888889, 3.88888888888889, 
3.88888888888889, 3.88888888888889, 3.88888888888889, 3.88888888888889, 
4.66666666666667, 4.66666666666667, 4.66666666666667, 4.66666666666667, 
4.66666666666667, 4.66666666666667, 4.66666666666667, 4.66666666666667, 
4.66666666666667, 4.66666666666667, 5.44444444444444, 5.44444444444444, 
5.44444444444444, 5.44444444444444, 5.44444444444444, 5.44444444444444, 
5.44444444444444, 5.44444444444444, 5.44444444444444, 5.44444444444444, 
6.22222222222222, 6.22222222222222, 6.22222222222222, 6.22222222222222, 
6.22222222222222, 6.22222222222222, 6.22222222222222, 6.22222222222222, 
6.22222222222222, 6.22222222222222, 7, 7, 7, 7, 7, 7, 7, 7, 7, 
7, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6.66666666666667, 6.66666666666667, 
6.66666666666667, 6.66666666666667, 6.66666666666667, 6.66666666666667, 
6.66666666666667, 6.66666666666667, 6.66666666666667, 6.66666666666667, 
8.33333333333333, 8.33333333333333, 8.33333333333333, 8.33333333333333, 
8.33333333333333, 8.33333333333333, 8.33333333333333, 8.33333333333333, 
8.33333333333333, 8.33333333333333, 10, 10, 10, 10, 10, 10, 10, 
10, 10, 10, 11.6666666666667, 11.6666666666667, 11.6666666666667, 
11.6666666666667, 11.6666666666667, 11.6666666666667, 11.6666666666667, 
11.6666666666667, 11.6666666666667, 11.6666666666667, 13.3333333333333, 
13.3333333333333, 13.3333333333333, 13.3333333333333, 13.3333333333333, 
13.3333333333333, 13.3333333333333, 13.3333333333333, 13.3333333333333, 
13.3333333333333, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16.6666666666667, 
16.6666666666667, 16.6666666666667, 16.6666666666667, 16.6666666666667, 
16.6666666666667, 16.6666666666667, 16.6666666666667, 16.6666666666667, 
16.6666666666667, 18.3333333333333, 18.3333333333333, 18.3333333333333, 
18.3333333333333, 18.3333333333333, 18.3333333333333, 18.3333333333333, 
18.3333333333333, 18.3333333333333, 18.3333333333333, 20, 20, 
20, 20, 20, 20, 20, 20, 20, 20, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0.777777777777778, 0.777777777777778, 0.777777777777778, 0.777777777777778, 
0.777777777777778, 0.777777777777778, 0.777777777777778, 0.777777777777778, 
0.777777777777778, 0.777777777777778, 1.55555555555556, 1.55555555555556, 
1.55555555555556, 1.55555555555556, 1.55555555555556, 1.55555555555556, 
1.55555555555556, 1.55555555555556, 1.55555555555556, 1.55555555555556, 
2.33333333333333, 2.33333333333333, 2.33333333333333, 2.33333333333333, 
2.33333333333333, 2.33333333333333, 2.33333333333333, 2.33333333333333, 
2.33333333333333, 2.33333333333333, 3.11111111111111, 3.11111111111111, 
3.11111111111111, 3.11111111111111, 3.11111111111111, 3.11111111111111, 
3.11111111111111, 3.11111111111111, 3.11111111111111, 3.11111111111111, 
3.88888888888889, 3.88888888888889, 3.88888888888889, 3.88888888888889, 
3.88888888888889, 3.88888888888889, 3.88888888888889, 3.88888888888889, 
3.88888888888889, 3.88888888888889, 4.66666666666667, 4.66666666666667, 
4.66666666666667, 4.66666666666667, 4.66666666666667, 4.66666666666667, 
4.66666666666667, 4.66666666666667, 4.66666666666667, 4.66666666666667, 
5.44444444444444, 5.44444444444444, 5.44444444444444, 5.44444444444444, 
5.44444444444444, 5.44444444444444, 5.44444444444444, 5.44444444444444, 
5.44444444444444, 5.44444444444444, 6.22222222222222, 6.22222222222222, 
6.22222222222222, 6.22222222222222, 6.22222222222222, 6.22222222222222, 
6.22222222222222, 6.22222222222222, 6.22222222222222, 6.22222222222222, 
7, 7, 7, 7, 7, 7, 7, 7, 7, 7), var1 = c("x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", 
"x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x1", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", 
"x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2", "x2"
), var2 = c("x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", "x3", 
"x3", "x3", "x3", "x3", "x3", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", "x4", 
"x4", "x4", "x4", "x4", "x4", "x4"), resp = c(49.855790574209, 
51.1750882867235, 52.494385999238, 53.8136837117525, 55.132981424267, 
56.4522791367815, 57.771576849296, 59.0908745618105, 60.410172274325, 
61.7294699868395, 56.5060300788685, 57.825327791383, 59.1446255038975, 
60.463923216412, 61.7832209289265, 63.102518641441, 64.4218163539555, 
65.74111406647, 67.0604117789845, 68.379709491499, 63.1562695835279, 
64.4755672960424, 65.7948650085569, 67.1141627210714, 68.4334604335859, 
69.7527581461004, 71.0720558586149, 72.3913535711294, 73.7106512836439, 
75.0299489961584, 69.8065090881873, 71.1258068007018, 72.4451045132163, 
73.7644022257308, 75.0836999382454, 76.4029976507599, 77.7222953632744, 
79.0415930757889, 80.3608907883034, 81.6801885008178, 76.4567485928468, 
77.7760463053613, 79.0953440178758, 80.4146417303903, 81.7339394429048, 
83.0532371554193, 84.3725348679338, 85.6918325804483, 87.0111302929628, 
88.3304280054773, 83.1069880975062, 84.4262858100207, 85.7455835225352, 
87.0648812350497, 88.3841789475642, 89.7034766600787, 91.0227743725932, 
92.3420720851077, 93.6613697976222, 94.9806675101367, 89.7572276021656, 
91.0765253146801, 92.3958230271947, 93.7151207397092, 95.0344184522237, 
96.3537161647382, 97.6730138772527, 98.9923115897672, 100.311609302282, 
101.630907014796, 96.4074671068251, 97.7267648193396, 99.0460625318541, 
100.365360244369, 101.684657956883, 103.003955669398, 104.323253381912, 
105.642551094427, 106.961848806941, 108.281146519456, 103.057706611485, 
104.377004323999, 105.696302036514, 107.015599749028, 108.334897461543, 
109.654195174057, 110.973492886572, 112.292790599086, 113.612088311601, 
114.931386024115, 109.707946116144, 111.027243828658, 112.346541541173, 
113.665839253687, 114.985136966202, 116.304434678716, 117.623732391231, 
118.943030103745, 120.26232781626, 121.581625528774, 44.8527240775983, 
46.1720217901128, 47.4913195026273, 48.8106172151418, 50.1299149276563, 
51.4492126401708, 52.7685103526853, 54.0878080651998, 55.4071057777143, 
56.7264034902288, 48.7344239681344, 50.0537216806489, 51.3730193931634, 
52.6923171056779, 54.0116148181924, 55.3309125307069, 56.6502102432214, 
57.9695079557359, 59.2888056682504, 60.6081033807649, 52.6161238586705, 
53.935421571185, 55.2547192836995, 56.574016996214, 57.8933147087285, 
59.212612421243, 60.5319101337575, 61.851207846272, 63.1705055587865, 
64.489803271301, 56.4978237492065, 57.817121461721, 59.1364191742355, 
60.45571688675, 61.7750145992646, 63.094312311779, 64.4136100242935, 
65.732907736808, 67.0522054493226, 68.3715031618371, 60.3795236397426, 
61.6988213522571, 63.0181190647716, 64.3374167772861, 65.6567144898006, 
66.9760122023151, 68.2953099148296, 69.6146076273441, 70.9339053398586, 
72.2532030523731, 64.2612235302787, 65.5805212427932, 66.8998189553077, 
68.2191166678222, 69.5384143803367, 70.8577120928512, 72.1770098053657, 
73.4963075178802, 74.8156052303947, 76.1349029429092, 68.1429234208147, 
69.4622211333293, 70.7815188458437, 72.1008165583582, 73.4201142708727, 
74.7394119833872, 76.0587096959017, 77.3780074084163, 78.6973051209308, 
80.0166028334453, 72.0246233113508, 73.3439210238653, 74.6632187363798, 
75.9825164488943, 77.3018141614088, 78.6211118739233, 79.9404095864378, 
81.2597072989523, 82.5790050114668, 83.8983027239813, 75.9063232018869, 
77.2256209144014, 78.5449186269159, 79.8642163394304, 81.1835140519449, 
82.5028117644594, 83.8221094769739, 85.1414071894884, 86.4607049020029, 
87.7800026145174, 79.7880230924229, 81.1073208049374, 82.4266185174519, 
83.7459162299664, 85.065213942481, 86.3845116549954, 87.7038093675099, 
89.0231070800245, 90.342404792539, 91.6617025050535, 55.0389923581682, 
55.076209045692, 55.1878591082632, 55.373942545882, 55.6344593585483, 
55.9694095462621, 56.3787931090235, 56.8626100468323, 57.4208603596887, 
58.0535440475926, 61.6892318628276, 61.7264485503514, 61.8380986129227, 
62.0241820505415, 62.2846988632078, 62.6196490509216, 63.0290326136829, 
63.5128495514918, 64.0710998643481, 64.703783552252, 68.3394713674871, 
68.3766880550108, 68.4883381175821, 68.6744215552009, 68.9349383678672, 
69.269888555581, 69.6792721183423, 70.1630890561512, 70.7213393690076, 
71.3540230569114, 74.9897108721465, 75.0269275596703, 75.1385776222415, 
75.3246610598603, 75.5851778725266, 75.9201280602404, 76.3295116230018, 
76.8133285608106, 77.371578873667, 78.0042625615709, 81.639950376806, 
81.6771670643297, 81.788817126901, 81.9749005645198, 82.2354173771861, 
82.5703675648999, 82.9797511276612, 83.4635680654701, 84.0218183783264, 
84.6545020662303, 88.2901898814654, 88.3274065689891, 88.4390566315604, 
88.6251400691792, 88.8856568818455, 89.2206070695593, 89.6299906323207, 
90.1138075701295, 90.6720578829859, 91.3047415708897, 94.9404293861248, 
94.9776460736486, 95.0892961362198, 95.2753795738386, 95.5358963865049, 
95.8708465742187, 96.2802301369801, 96.7640470747889, 97.3222973876453, 
97.9549810755492, 101.590668890784, 101.627885578308, 101.739535640879, 
101.925619078498, 102.186135891164, 102.521086078878, 102.93046964164, 
103.414286579448, 103.972536892305, 104.605220580209, 108.240908395444, 
108.278125082967, 108.389775145539, 108.575858583158, 108.836375395824, 
109.171325583538, 109.580709146299, 110.064526084108, 110.622776396964, 
111.255460084868, 114.891147900103, 114.928364587627, 115.040014650198, 
115.226098087817, 115.486614900483, 115.821565088197, 116.230948650958, 
116.714765588767, 117.273015901624, 117.905699589528, 50.0359258615575, 
50.0731425490813, 50.1847926116525, 50.3708760492713, 50.6313928619376, 
50.9663430496514, 51.3757266124128, 51.8595435502216, 52.417793863078, 
53.0504775509819, 53.9176257520936, 53.9548424396173, 54.0664925021886, 
54.2525759398074, 54.5130927524737, 54.8480429401875, 55.2574265029488, 
55.7412434407577, 56.2994937536141, 56.9321774415179, 57.7993256426296, 
57.8365423301534, 57.9481923927247, 58.1342758303435, 58.3947926430098, 
58.7297428307236, 59.1391263934849, 59.6229433312938, 60.1811936441501, 
60.813877332054, 61.6810255331657, 61.7182422206895, 61.8298922832607, 
62.0159757208795, 62.2764925335458, 62.6114427212596, 63.020826284021, 
63.5046432218298, 64.0628935346862, 64.6955772225901, 65.5627254237018, 
65.5999421112255, 65.7115921737968, 65.8976756114156, 66.1581924240819, 
66.4931426117957, 66.9025261745571, 67.3863431123659, 67.9445934252223, 
68.5772771131261, 69.4444253142378, 69.4816420017616, 69.5932920643329, 
69.7793755019516, 70.039892314618, 70.3748425023318, 70.7842260650931, 
71.268043002902, 71.8262933157583, 72.4589770036622, 73.3261252047739, 
73.3633418922977, 73.4749919548689, 73.6610753924877, 73.921592205154, 
74.2565423928679, 74.6659259556292, 75.149742893438, 75.7079932062944, 
76.3406768941983, 77.20782509531, 77.2450417828337, 77.356691845405, 
77.5427752830238, 77.8032920956901, 78.1382422834039, 78.5476258461653, 
79.0314427839741, 79.5896930968305, 80.2223767847343, 81.089524985846, 
81.1267416733698, 81.2383917359411, 81.4244751735599, 81.6849919862262, 
82.01994217394, 82.4293257367013, 82.9131426745102, 83.4713929873665, 
84.1040766752704, 84.9712248763821, 85.0084415639059, 85.1200916264771, 
85.3061750640959, 85.5666918767622, 85.9016420644761, 86.3110256272374, 
86.7948425650462, 87.3530928779026, 87.9857765658065)), .Names = c("x", 
"y", "var1", "var2", "resp"), row.names = 101:500, class = "data.frame")

Answer 1

Я столкнулся с двумя проблемами:

1) Мой истинный набор данных генерируется через fit <- lm(x ~ y)с последующим созданием нового набора входных данных через expand.gridи затем создаю мои данные графика с predict(fit, newdata), Странно, если я не обойду x а также y точки, я не могу сгенерировать график (полный код для создания моих данных графика ниже).

2) При построении одного geom_tile сюжет, высота / ширина плитки установлены для заполнения пространства. При создании ограненного набора плиточных участков кажется, что height а также width аргументы в пользу geom_tile() по умолчанию на что-то другое. Я бы сказал, что по умолчанию они имеют наименьший диапазон, но на самом деле ни один график не заполняет всю ширину или высоту окна полного фасета... так что это не так.

Извинения за приведенный выше пример не воспроизводимы. Я этого не ожидал dput() Я бы не стал создавать идентичный набор данных, и было бы гораздо проще просто вставить вывод этого, чем кто-то запустить весь код ниже.

---

Полный код для генерации набора данных:

set.seed(42)
x1 <- rnorm(20)
x2 <- runif(20)
x3 <- rpois(20,10)
x4 <- rexp(20)
y <- 10 + 2*x1 + 3*x2^2 + 4*x3 +5*x4 + rnorm(20, sd=0.1)

dat <- data.frame(x1, x2, x3, x4, y)

# vector of variable names for easy data.frame column naming later
var_names <- c("x1", "x2", "x3", "x4")

# possible combinations of four variables
combis <- combn(1:4, 2)
combis <- rbind(combis, combis[, 6:1])

# steps to generate for the contour using `rep(min, max, length.out = n)`
n <- 100

#fit the model
fit <- lm(y~x1+I(x2^2)+x3+x4, data=dat)

# range values for when variable is featured on an axis
mins_maxs <- data.frame(x1 = c(-3, 3),
                        x2 = c(0, 1),
                        x3 = c(5, 20),
                        x4 = c(0, 7))

# values to hold for plots in which variables are not on an axis
holds <- c(0, 0.5, 10, 5)

sim_data <- list()
sim_data <- lapply(seq_len(ncol(combis)), function (i) {
  sim_data[[i]] <- expand.grid(seq(mins_maxs[1, combis[1, i]], 
                                   mins_maxs[2, combis[1, i]], length.out = n),
                               seq(mins_maxs[1, combis[2, i]], 
                                   mins_maxs[2, combis[2, i]], length.out = n),
                               holds[combis[3, i]],
                               holds[combis[4, i]])
} )

# we create a new data frame for the data set we want to plot
# for each contour of interest, we want the first two columns, as the second two
# were only created for the sake of feeding into our fit lm 
# we'll also create a vector for facetting using paste()
plot_data <- list()
plot_data <- lapply(1:ncol(combis), function(i) {
  plot_data[[i]] <- sim_data[[i]][, 1:2]
  plot_data[[i]]$var1 <- rep(var_names[combis[1, i]],
                             nrow(plot_data[[i]]))
  plot_data[[i]]$var2 <- rep(var_names[combis[2, i]],
                                   nrow(plot_data[[i]]))
  return(plot_data[[i]])
} )

# now we rename the columns of plot_data
plot_data <- lapply(1:length(plot_data), function(i) {
  names(plot_data[[i]]) <- c("x", "y", "var1", "var2")
  return(plot_data[[i]])
} )

# similarly, we need to re-name the sim_data columns so we can rbind them
# and predict new values using our fit lm
sim_data <- lapply(1:length(sim_data), function(i) {
  names(sim_data[[i]]) <- var_names[combis[, i]]
  return(sim_data[[i]])
} )


# collapse the separate lists into one data.frame
plot_data <- do.call(rbind, plot_data)
sim_data <- do.call(rbind, sim_data)

# create a vector of predictions using sim_data
plot_data$resp <- predict(fit, sim_data)

---

На данный момент, если кто-то пытается построить с помощью plot_dataмы получаем это:

library(ggplot2)
p <- ggplot(plot_data, aes(x = x, y = y, z = resp))
p <- p + geom_tile(aes(fill = resp))
p <- p + facet_wrap(var2 ~ var1, scales = "free", ncol = 3) + theme_bw()

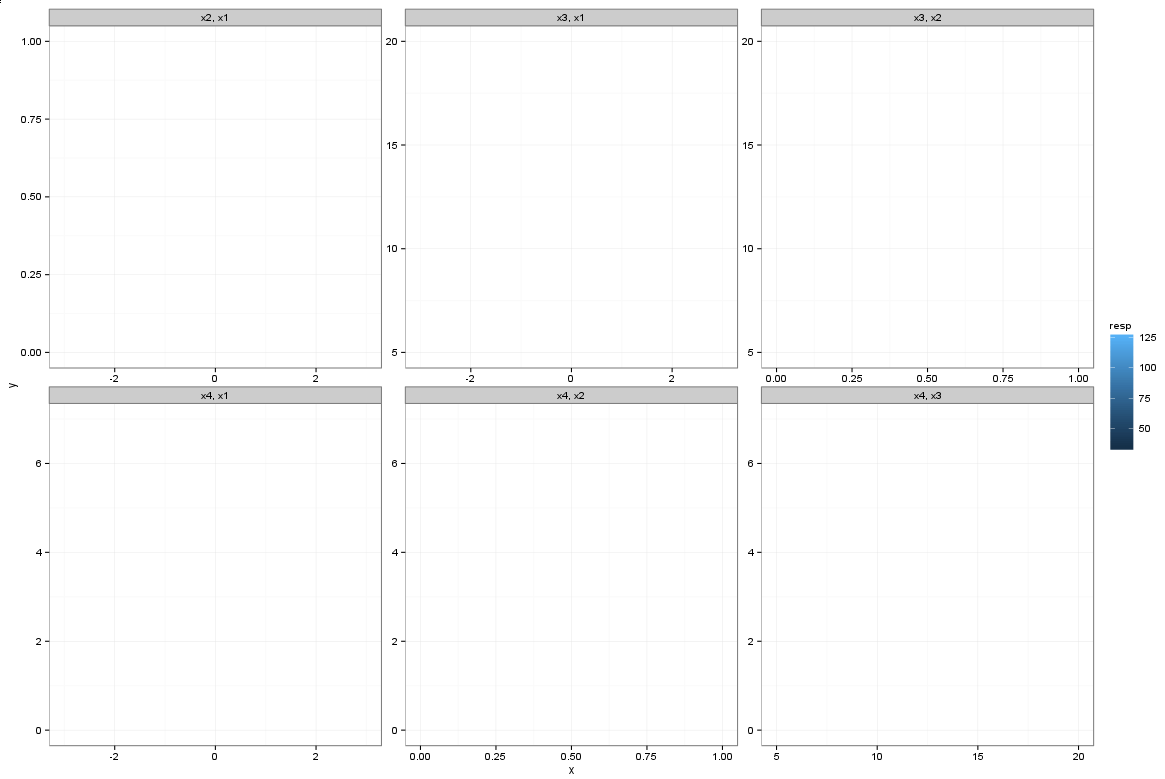
Если мы округлим данные, мы получим что-то еще:

plot_data_round <- plot_data
plot_data_round[, c("x", "y")] <- round(plot_data_round[, c("x", "y")], 5)

# same plot call as above
p <- ggplot(plot_data_round, aes(x = x, y = y, z = resp))
p <- p + geom_tile(aes(fill = resp))
p <- p + facet_wrap(var2 ~ var1, scales = "free", ncol = 3) + theme_bw()

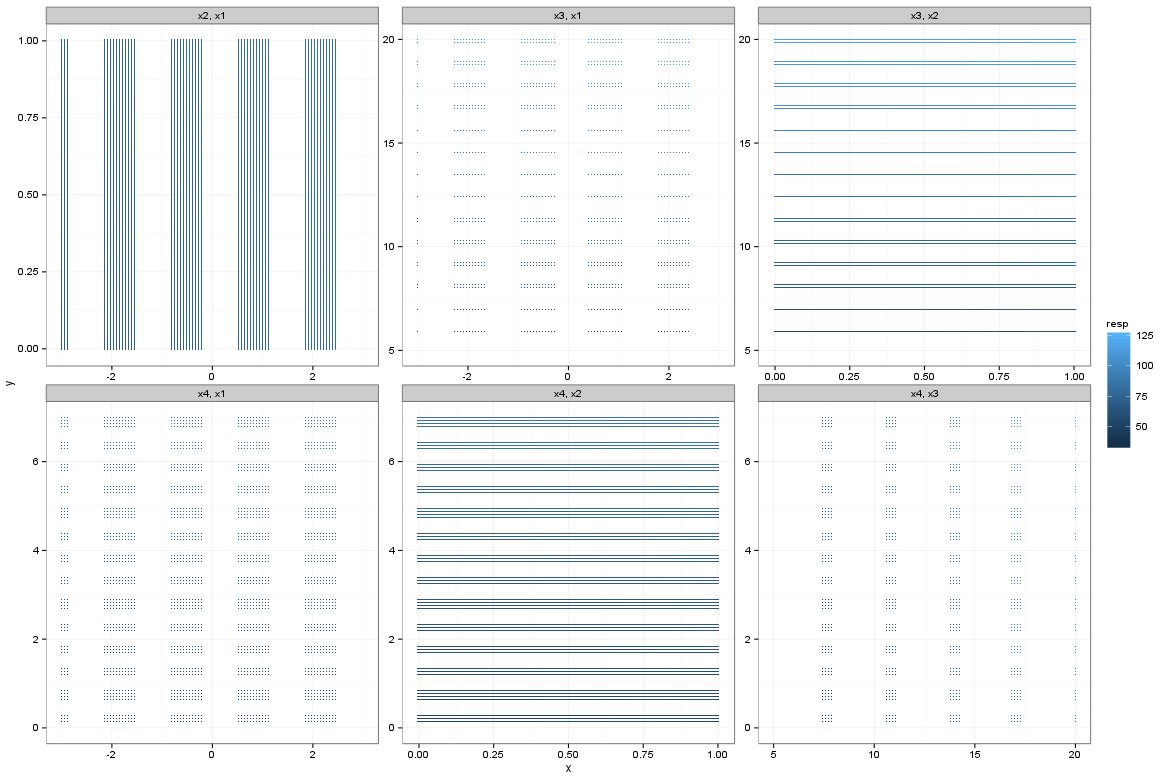
Если мы возьмем неокругленные данные и добавим векторы для сохранения высоты и ширины, мы вернемся к пустому фасетному графику, как только неокругленные данные.

plot_data_hw <- plot_data
hw <- ddply(plot_data, .(var1, var2), summarize,
            height = (max(y) - min(y))/n, width = (max(x) - min(x))/n)
plot_data_hw <- merge(plot_data_hw, hw, by = c("var1", "var2"), all.x = T)
# verify using same plot call and plot_data_hw

Если мы объединим округление и height а также width Значения на фасет взаимодействия, мы получаем желаемый результат (добавив height/width аргументы geom_tile()):

plot_data_hw_round <- merge(plot_data_round, hw, by = c("var1", "var2"), all.x = T)
p <- ggplot(plot_data_hw_round, aes(x = x, y = y, z = resp))
p <- p + geom_tile(aes(fill = resp, height = height, width = width))
p <- p + facet_wrap(var2 ~ var1, scales = "free", ncol = 3) + theme_bw()

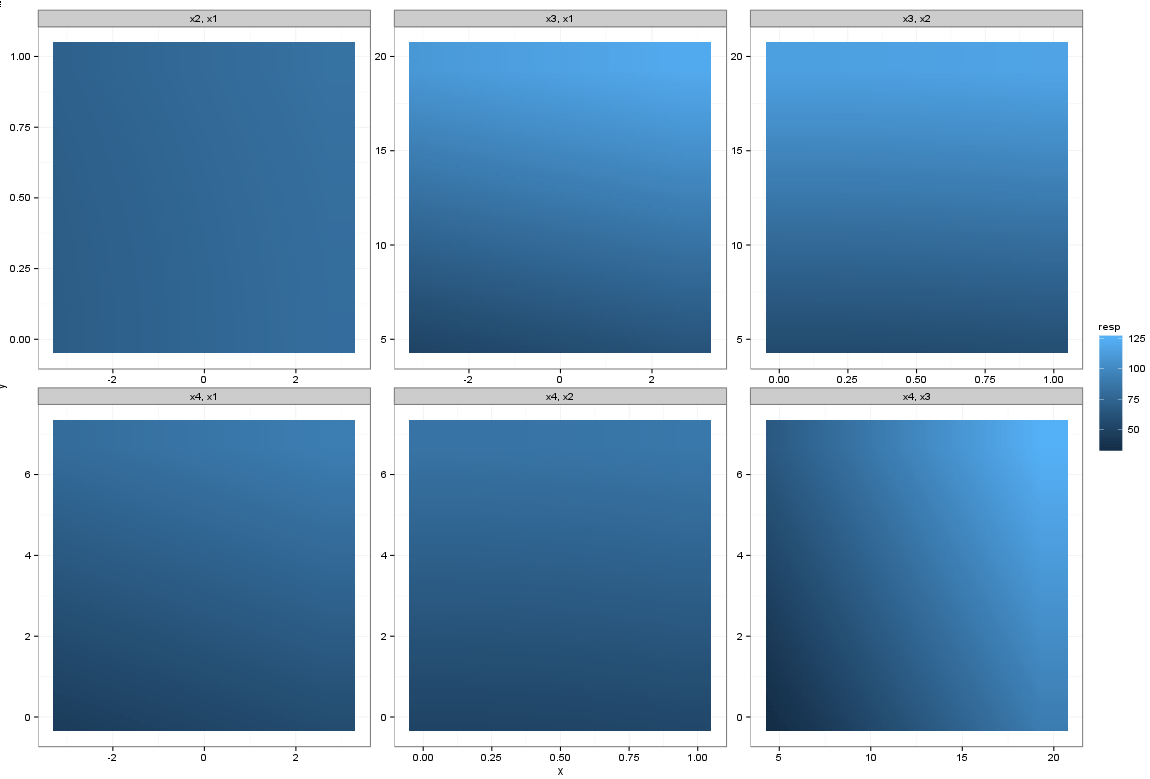
Итак, вот оно. Я собираюсь подать отчет об ошибке округления, поскольку это кажется мне довольно странным. Возможно, что-то еще происходит, но если это из-за точности с плавающей запятой или чего-то еще, Хэдли все еще может заинтересоваться.