Смущает процесс проверки P2b на бумаге.
Я читаю газету Paxos, сделанную простой, но застрявшую на части для P2b.
Содержание правила P2b:
Если выбрано предложение со значением v, то каждое предложение с более высоким номером, выданное любым заявителем, имеет значение v.
И это доказательная часть Лесли Лэмпорта:
Чтобы выяснить, как удовлетворить P2b, давайте рассмотрим, как мы докажем, что оно выполняется. Мы предположили бы, что выбрано какое-то предложение с номером m и значением v, и покажем, что любое предложение, выданное с номером n> m, также имеет значение v. Мы упростили бы доказательство, используя индукцию по n, чтобы мы могли доказать, что предложение n имеет значение v при дополнительном допущении, что каждое предложение, выпущенное с номером в m., (n-1) имеет значение v, где i., j обозначает набор чисел от i до j. Чтобы предложение, пронумерованное m, было выбрано, должен быть некоторый набор C, состоящий из большинства акцепторов, чтобы каждый акцептор в C принял его. Комбинируя это с предположением индукции, гипотеза о том, что выбрано m, предполагает:
Каждый акцептор в C принял предложение с номером в m . . (n-1), и каждое предложение с номером в m . . (n-1), принятое любым акцептором, имеет значение v
Итак, индукционный процесс:
- Базовый случай: выбрано предложение m со значением v
- Индуктивный шаг: любое предложение в номере m . . (n-1) имеет значение v
Почему это означает, что:
Каждый акцептор в C принял предложение с номером в m . . (n-1)
Я просто не могу преодолеть разрыв, почему каждый акцептор в C должен принять предложение с номером в m . . (n-1)?
P1 гарантирует, что акцептор должен принять первое полученное предложение,P2 гарантирует, что акцепторы могут принять только предложения с более высоким номером с выбранным значением, но я просто не понимаю смысл подразумеваемого утверждения.
2 ответа
Вот графическое объяснение всего доказательства правильности.
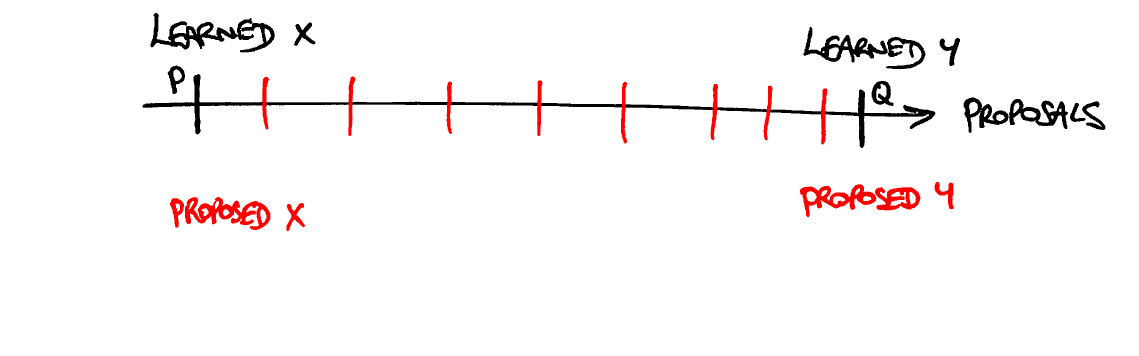
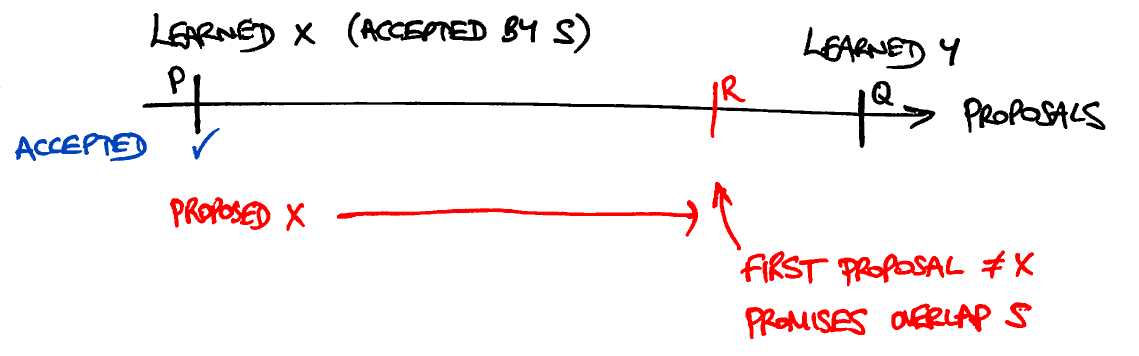
- Предположим, что значения были получены для двух предложений, пронумерованных P и Q, где P
- Кроме того, предположим для противоречия, что выученное значение для P было X, а выученное значение для Q было Y, где X ≠ Y:
- Это означает, что значения, предложенные для P и для Q, были X и Y соответственно. Каждое предложение может иметь не более одного значения:
- Теперь рассмотрим все другие предложения, которые были сделаны между P и Q:
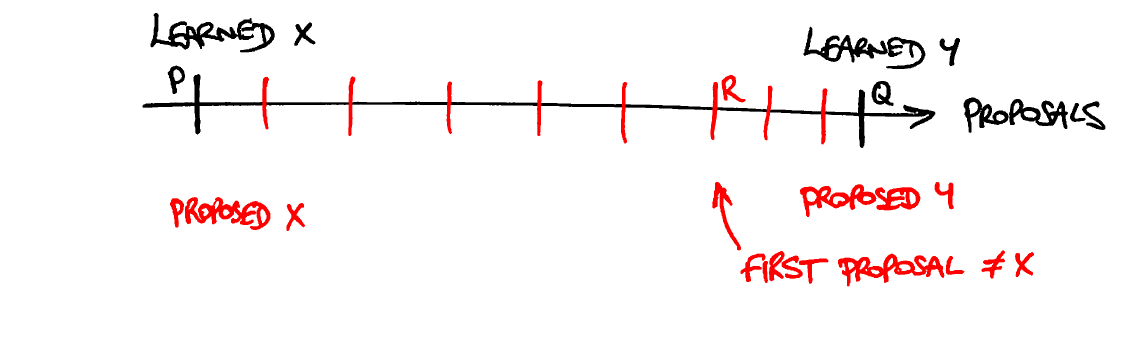
- Пусть R будет первым предложением, значение которого было ≠X. Надеемся, что P
- Другими словами, предложения с номерами ≥ P и
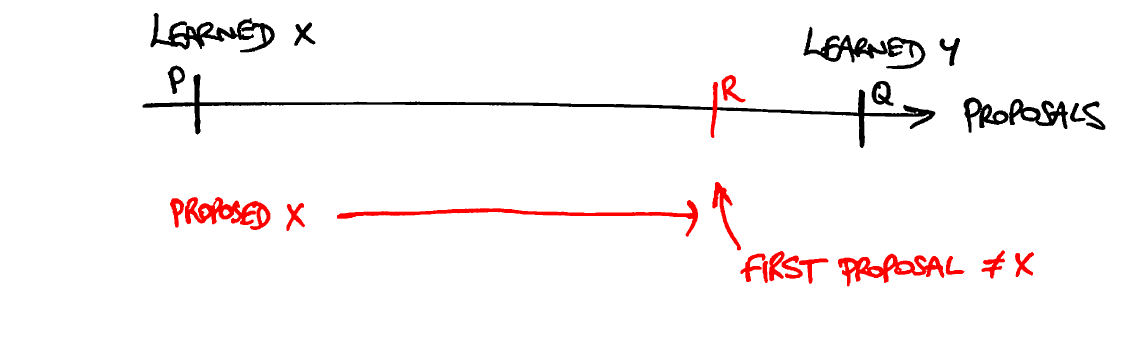
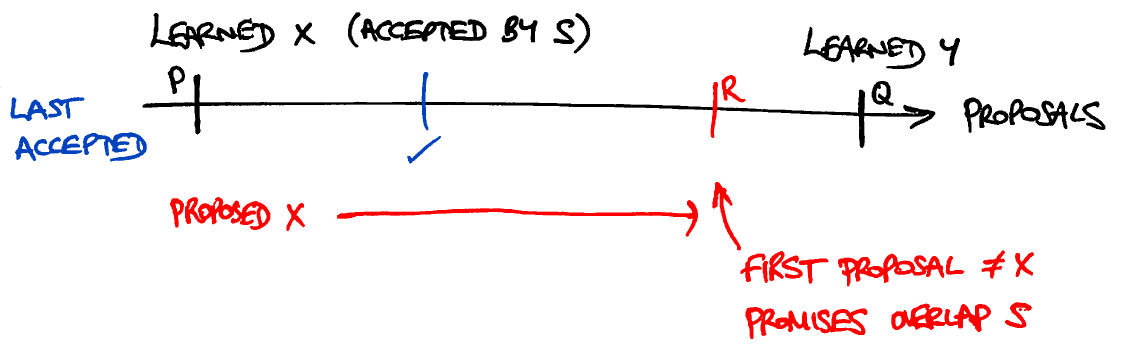
- Пусть S будет набором узлов, которые отправили сообщения фазы 2b в P. (S в вашем вопросе называется C, но я уже нарисовал эти картинки, поэтому придерживаюсь S). Поскольку большинство пересекаются, этот набор узлов должен перекрывать набор узлов, которые отправили сообщения фазы 1b в R:
- Созерцайте один из узлов, который был в перекрытии. Он должен был отправить свое сообщение фазы 2b в P перед отправкой своего сообщения фазы 1b в R, потому что это то, для чего предназначены сообщения фазы 1b.
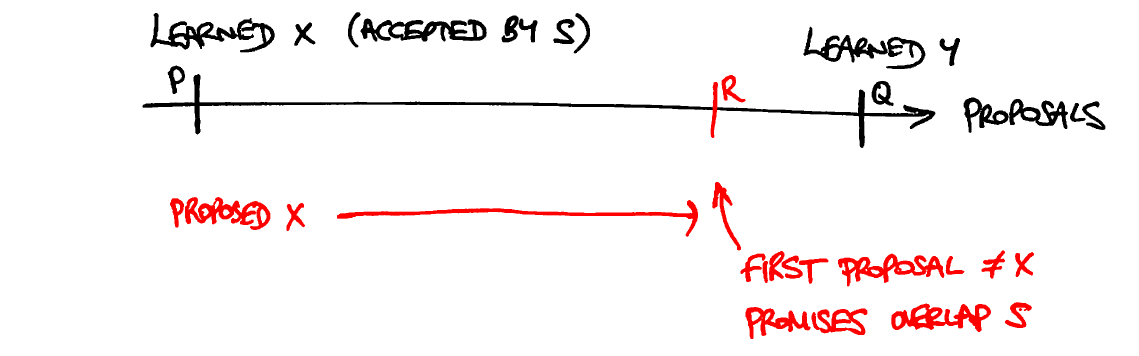
- Возможно, он также отправил сообщение фазы 2b для предложения, пронумерованного>P, но не смог отправить сообщение для предложения, пронумерованного ≥R, потому что это правило для сообщений фазы 1b. Но все предложения с ≥ P и
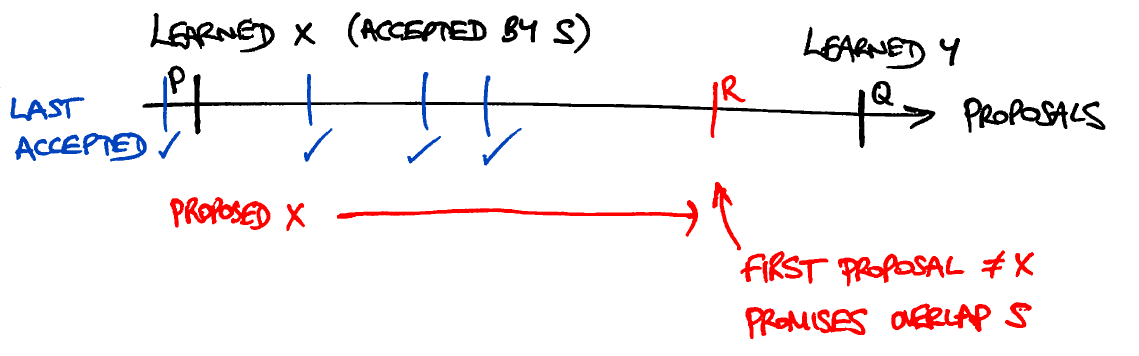
- Теперь рассмотрите все другие узлы, которые отправили сообщения фазы 1b для предложения R. Некоторые из них, возможно, не приняли никакого предыдущего предложения; некоторые, возможно, приняли предложения, пронумерованные
В этом заключается противоречие: по правилам для сообщений фазы 2а это означает, что значение, предложенное в точке R, должно быть X в конце концов.
Это может показаться вам существенно отличным от доказательства, приведенного в статье Paxos Made Simple, поскольку, похоже, оно работает противоречием и в нем нет явной индукции. На самом деле, техника "предположим, что существует контрпример, а затем рассмотрим наименьшее из таких" на шаге 5, на самом деле является просто скрытой индукцией, и мой опыт показывает, что это более доступный способ ее представления. Это интересное упражнение - превратить этот шаг в явную индукцию, если вам нравится такая вещь.
Упомянутый в вашем вопросе набор C - это набор акцепторов, отправивших сообщения фазы 2b для принятия предложения в P. Это не обязательно тот же набор, что и те, которые отправили сообщения фазы 1b в R, но эти наборы пересекаются, и это важный фактор.
Это действительно легко зацикливаться на деталях, учитывая язык в этой статье. Я предлагаю попробовать Понимание Паксос вместо этого. Это гораздо более многословно, но в нем рассматриваются как и почему, а также окружающие вопросы для практического использования алгоритма без набора обозначений или надстрочных знаков.
Каждый акцептор в C принял предложение с номером в m ..(n - 1) Поскольку предложение m со значением v было выбрано, должен быть некоторый набор C, состоящий из большинства акцепторов, чтобы каждый акцептор в C принял его, и m ..(n - 1) содержит m