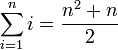Почему переменные "i" и "j" используются для счетчиков?

Question

Я знаю, что это может показаться глупым вопросом, но мне слишком любопытно не задавать вопросы...

Почему "i" и "j" стали переменными для использования в качестве счетчиков в большинстве структур управления?

Хотя здравый смысл говорит мне, что они похожи на X, который используется для представления неизвестных значений, я не могу не думать, что должна быть причина, по которой всех учат одинаково снова и снова.

Это потому, что на самом деле это рекомендуется для передового опыта или конвенции, или за этим стоит какая-то неясная причина?

На всякий случай я знаю, что могу дать им любое имя, и имена переменных не имеют значения.

Answer 1

В конечном итоге это исходит из математики: для обозначения суммирования традиционно используется i для первого индекса, j для второго и так далее. Пример (из http://en.wikipedia.org/wiki/Summation):

Он также используется таким образом для коллекций вещей, например, если у вас есть набор переменных x₁, x₂,... x_n, тогда произвольная переменная будет известна как x_i.

Что касается того, почему это так, я думаю, что SLaks является правильным, и это потому, что я первая буква в Index.

Answer 2

Я верю, что это восходит к Фортрану. Переменные, начинающиеся с I по Q, были по умолчанию целочисленными, остальные были действительными. Это означало, что I была первой целочисленной переменной, и J второй и т. д., поэтому они упали на использование в петлях.

Answer 3

Математики использовали i,j,k для обозначения целых чисел в алгебре (индексы, серии, суммирования и т. Д.) Задолго до появления компьютеров (например, 1836 или 1816) (это источник значений по умолчанию типа переменных FORTRAN). Привычка использовать буквы от конца алфавита (...,x,y,z) для неизвестных переменных и от начала (a, b, c...) для констант обычно приписывается Рене Декарту(см. также здесь), поэтому я предполагаю, что i,j,k...n (в середине алфавита) для целых чисел, вероятно, тоже из-за него.

Answer 4

Я = целое число

Приходит из Фортрана, где целочисленные переменные должны были начинаться с букв от I до N, а реальные переменные начинались с других букв. Таким образом, я был первым и самым коротким целочисленным именем переменной. Фортран был одним из первых широко распространенных языков программирования, и привычки, разработанные программистами при его использовании, были перенесены на другие языки.

РЕДАКТИРОВАТЬ: У меня нет проблем с ответом, который он вытекает из математики. Несомненно, именно здесь дизайнеры Fortran черпали свое вдохновение. Во всяком случае, для меня факт, что когда я начал программировать на Фортране, мы использовали I, J, K, ... для счетчиков циклов, потому что они были короткими, а первые юридически допустимые имена переменных для целых чисел. Как второкурсник в HS я, вероятно, слышал о Декарте (и очень немногих других), но при программировании очень мало имел отношения к математике. Фактически, первый курс, который я выбрал, назывался "Фортран для бизнеса" и преподавался не на математическом факультете, а на факультете бизнеса / экономики.

Для меня, по крайней мере, именование переменных не имело ничего общего с математикой, но все из-за привычек, которые я приобрел для написания кода на Фортране, который я перенес на другие языки.

Answer 5

i stands for I ndex.
j идет после i,

Answer 6

Эти символы использовались в качестве матричных индексов в математике задолго до того, как были изобретены электронные компьютеры.

Answer 7

Я думаю, что он, скорее всего, получен из индекса (в математическом смысле) - он обычно используется в качестве индекса в суммах или других операциях на основе множеств и, скорее всего, использовался таким образом еще до появления языков программирования.

Answer 8

В математике предпочтение отдается использованию последовательных букв в алфавите для "анонимных" переменных, используемых аналогичным образом. Следовательно, не только "i, j, k", но также "f, g, h", "p, q, r", "x, y, z" (редко с префиксом "u, v, w"), и "α, β, γ".

Теперь "f, g, h" и "x, y, z" не используются свободно: первый предназначен для функций, второй - для измерений. "p, q, r" также часто используются для функций.

Тогда есть другие ограничения на доступные последовательности: "l" и "o" избегаются, потому что они слишком похожи на "1" и "0" во многих шрифтах. "t" часто используется для времени, "d & δ" для дифференциалов и "a, s, m, v" для физических мер ускорения, смещения, массы и скорости. Это оставляет не так много пробелов из трех последовательных букв без нежелательных ассоциаций в математике для индексов.

Затем, как заметили несколько других, условные обозначения из математики оказали сильное влияние на ранние условные обозначения, и "α, β, γ" не были доступны во многих ранних наборах символов.

Answer 9

Я нашел другой возможный ответ, который может быть, что я, J и K приходят из Hamilton's Quaternions,

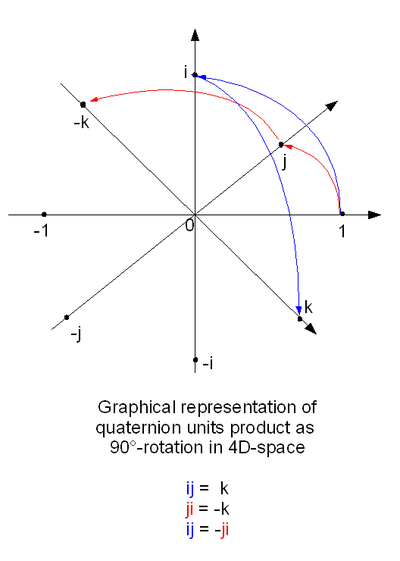
Эйлер выбрал меня за воображаемую единицу.

Гамильтону понадобилось еще два квадратных корня из -1: ii = jj = kk = ijk = -1

Гамильтон был действительно влиятельным, и кватернионы были стандартным способом сделать трехмерный анализ до 1900 года. К тому времени математики уже привыкли думать о (ijk) как о согласованном множестве.Векторное исчисление заменило кватернионный анализ в 1890-х годах, потому что это был лучший способ написать уравнения Максвелла. Но люди, как правило, записывали векторные величины следующим образом: (3i-2j+k) вместо (3,-2,1), Так (ijk) стал стандартным базисным вектором в R^3.

Наконец, физики начали использовать теорию групп для описания симметрий в системах дифференциальных уравнений. Итак, (ijk) начал обозначать "векторы, которые обмениваются группами перестановок", затем перешел к "индексным вещам, которые принимают все возможные значения в некотором указанном наборе", что в основном и означает в цикле for.

Answer 10

Отбрасывая (немного предвзято)

a seems an array
b seems another array 
c seems a language name
d seems another language name
e seems exception
f looks bad in combination with "for" (for f, a pickup?)
g seems g force
h seems height

---

i seems an index                    
j seems i (another index)

---

k seems a constant k
l seems a number one (1) 
m seems a matrix
n seems a node
o seems an output
p sounds like a pointer
q seems a queue
r seems a return value
s seems a string
t looks like time
u reserved for UVW mapping or electic phase 
v reserved for UVW mapping or electic phase or a vector
w reserved for UVW mapping or electic phase or a weight
x seems an axis (or an unknown variable)
y seems an axis
z seems a third axis

Answer 11

В один солнечный день Архимед обдумал (как обычно было в солнечные дни) и столкнулся со своим приятелем Эратосфеном.

Архимед сказал: "Приветствую Архимеда и Эратосфена! Я пытаюсь найти решение для соотношения нескольких сферических твердых тел в равновесии. Я хочу перебирать эти тела несколько раз, но у меня ужасное время, чтобы отследить сколько итераций я сделал!

Эратосфен сказал: "Почему, Архимед, ты, зрелая слива шутника, ты можешь просто пометить последовательные ряды строк на песке, каждый из которых отслеживает количество итераций, которые ты сделал за итерацию!"

Архимед закричал всему миру, что его великий друг, несомненно, был ярким маяком разума для того, чтобы придумать такое простое решение. Но Архимед заметил, что ему нравится ходить кругами вокруг своей песчаной ямы, пока он размышляет. Таким образом, был риск потерять след, какой ряд был сверху, а какой снизу.

"Возможно, мне следует пометить эти строки буквой алфавита рядом с краем, чтобы я всегда знал, какая строка какая! Что вы об этом думаете?" он спросил, затем добавил: "Но, Эратосфен... какие буквы я буду использовать?"

Эратосфен был уверен, что не знает, какие буквы будут лучше, и сказал так же Архимеду. Но Архимед был неудовлетворен и продолжал подталкивать бедного библиотекаря, чтобы выбрать, по крайней мере, две буквы, которые ему потребуются для его текущего решения сферного равновесия.

Эратосфен, наконец усталый от непрекращающейся просьбы о двух письмах, закричал: "Я НЕ ЗНАЮ!!!"

Поэтому Архимед выбрал первые две буквы в восклицательном предложении Эратосфена и поблагодарил своего друга за вклад.

---

Эти символы были быстро приняты древнегреческими разработчиками Java, а остальное, ну... история.

Answer 12

Я думаю, это потому, что многие циклы используют переменную типа Int для подсчета, например

for (int i = 0; etc

и когда вы печатаете, вы на самом деле произносите это в своей голове (например, когда вы читаете), поэтому в уме вы говорите "int...."

и когда вам нужно написать письмо сразу после этого "int....", вы говорите / набираете "i", потому что это первая буква, о которой вы думаете, когда только что сказали "int".

как вы пишете слово детям, которые начинают учиться читать слова, написанные для них, используя имена, например:

СЛОВО заклинания Уильям W, ОК O, Рубин R, Готово D

Итак, вы говорите Int I, Double d, Float f, string s и т. Д. На основе первой буквы.

И j используется, потому что, когда вы сделали int I, J следует сразу за ним.

Answer 13

Я думаю, что это сочетание других упомянутых причин:

Для начала, "i" обычно использовалось математиками в их обозначениях, и в первые дни вычислений с языками, которые не были двоичными (то есть должны были быть проанализированы и лексированы некоторым способом), подавляющее большинство пользователей компьютеров были также математики (... и ученые и инженеры), так что нотация стала использоваться в компьютерных языках для циклов программирования, и с тех пор как-то застряла.

Объедините это с тем фактом, что пространство экрана в те самые первые годы было очень ограничено, так же как и память, имело смысл сохранять более короткие имена переменных.

Answer 14

Я = итератор, я = индекс, я = целое число

Что бы вы ни считали "я", оно все еще "отвечает всем требованиям".

Кроме того, если у вас нет только одной строки кода в этом цикле, вы, вероятно, должны называть переменную iterator/index/integer чем-то более значимым. Нравится: employeeIndex

Кстати, я обычно использую "i" в моих простых циклах итераторов; если, конечно, он не содержит несколько строк кода.

Answer 15

Я = йота, j = йот; оба небольших изменения.

йота - самая маленькая буква в греческом алфавите; в английском языке его значение связано с небольшими изменениями, как, например, "ни на йоту" (из фразы в Новом Завете: "пока небо и земля не пройдут, ни йота, ни точка не перейдут от закона") (Мф 5:18)).

Счетчик представляет небольшое изменение значения.

И из йоты происходит йот (iot), который также является синонимом небольшого изменения.

ср http://en.wikipedia.org/wiki/Iota

Answer 16

Возможно исторический?

FORTRAN, возможно, первый язык высокого уровня, определил i,j,k,l,m как целочисленные типы данных по умолчанию, и циклы могут управляться только целочисленной переменной, соглашение продолжается?

например:

сделать 100 я = J,100,5 .... 100 продолжить....

Answer 17

Ну из математики: (для латинских букв)

a, b: используется как константа или как целое число для рационального числа
с: константа
д: производная
е: номер Эйлера
f, g, h: функции
i,j,k: индексы (также единичные векторы и кватернионы)
л: обычно не используется. выглядит как 1
m, n: строки и столбцы матриц или целые числа для рациональных чисел
o: также не используется (если вы не в небольшом обозначении o)
p, q: часто используется в качестве простых чисел
r: иногда пространственное изменение переменной, иногда связанное с простыми числами
s, t: пространственные и временные переменные или s используется как замена переменной для t
u, v, w: изменение переменной
x,y,z: переменные

Answer 18

Я полагаю, много возможных основных причин:

• математики используют i а также j для натуральных чисел в формулах (те, которые используют сложные числа редко, по крайней мере), так что это перенесено на программирование
• из С, i намеки на int, И если вам нужен другой int затем i2 просто слишком долго, поэтому вы решили использовать j,
• есть языки, где первая буква определяет тип, и i тогда integer,

Answer 19

Это происходит из Фортрана, где i,j,k,l,m,n являются неявно целыми числами.

Answer 20

Это определенно происходит от математики, которая давно предшествовала компьютерному программированию.

Так откуда же взяться в математике? Мое совершенно необразованное предположение состоит в том, что, как сказал один из них, математики любят использовать буквенные кластеры для похожих вещей - f, g, h для функций; x, y, z для числовых переменных; p, q, r для логических переменных; u, v, w для других наборов переменных, особенно в исчислении; а, б, в для многих вещей. i, j, k пригодится для итерационных переменных, и это исчерпывает возможности. Почему не м, н? Ну, они используются для целых чисел, но чаще всего конечные точки итераций, а не сами итерационные переменные.

Кто-то должен спросить историка математики.

Answer 21

Счетчики так распространены в программах, и на заре вычислительной техники все было дороже...
Программисты, естественно, пытались сохранить пиксели, и "i" требовало меньше пикселей, чем любая другая буква для представления. (Математики, будучи ленивыми, выбрали его по той же причине - как самый маленький глиф).
Как уже говорилось ранее, "j" естественно следовал...

:)

Answer 22

Я использую это по ряду причин.

• Обычно мои циклы основаны на int, поэтому вы делаете полный треугольник на клавиатуре, набирая "int i", за исключением места, которое я обрабатываю большим пальцем. Это очень быстрая последовательность ввода.

• "I" может обозначать итератор, целое число, приращение или индекс, каждый из которых имеет логический смысл.

Если оставить в стороне мои личные использования, теория о том, что она получена из FORTRAN, верна, где целые числа используют буквы I - N.

Answer 23

Я изучил FORTRAN в корпорации Control Data Corp. 3100 в 1965 году. Предполагалось, что переменные, начинающиеся с 'I' до 'N', являются целыми числами. Пример: "IGGY" и "NORB" были целыми числами, "XMAX" и "ALPHA" были числами с плавающей точкой. Однако вы можете переопределить это через явное объявление.