Как нарисовать фигуру (эллипс или овал) по некоторым точкам и рассчитать ее площадь?

Question

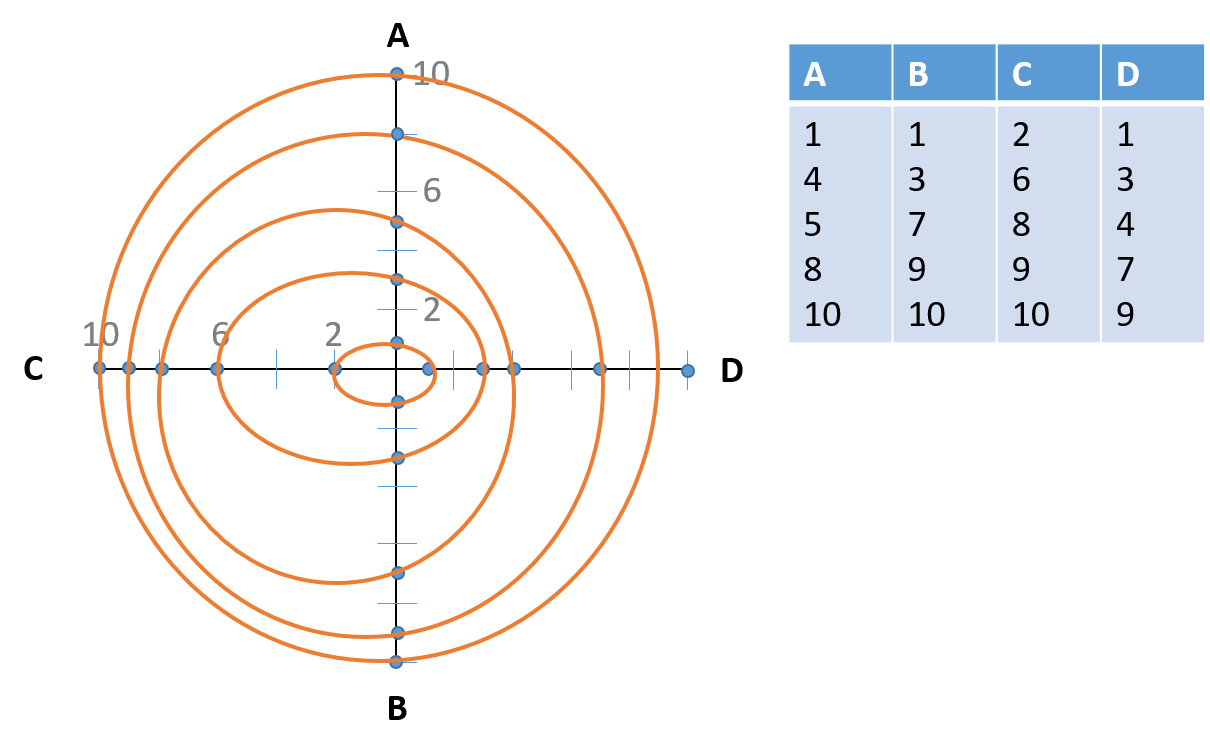
Я пытаюсь построить кольца деревьев и рассчитать их площади. Однако я заметил, что на самом деле не все кольца имеют симметричные радиусы как круг. У меня есть данные измерений 4 радиусов, и я хотел бы построить кольца (или любую подобную форму), следуя каждой точке каждого радио, как этот пример (этот рисунок был сделан вручную с векторами в PowerPoint):

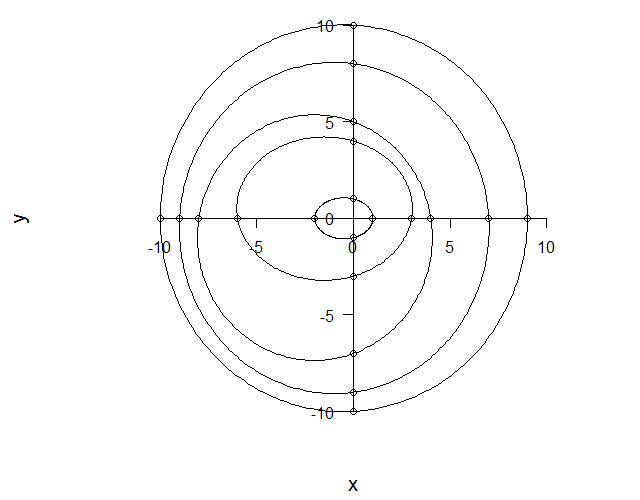
проблема в том, что в РИ нашли только возможность построить эти кольца с circles вариант из symbols() функция, и я получил этот график: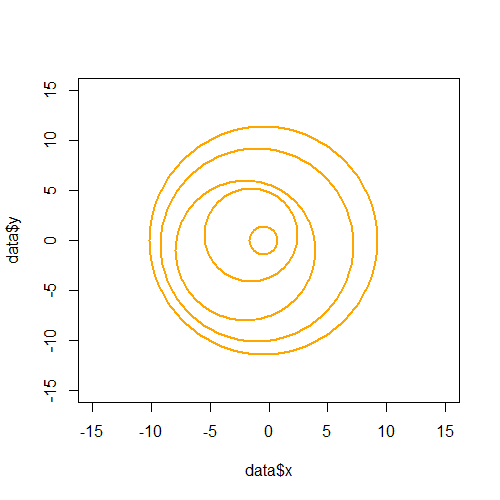

используя этот R скрипт:

data <- data.frame(
a = c(1,4,5,8, 10),
b = c(1, 3,7,9, 10),
c = c(2, 6, 8, 9 ,10),
d = c(1, 3, 4, 7, 9) )

data$y <- (data$a - data$b)/2 # y position
data$x <- (data$d - data$c)/2 # x position
data$z <- rowMeans(data[,1:4]) # radio length

symbols(x = data$x, y = data$y, circles=data$z, 
        xlim = c(-10, 10)*1.5, ylim = c(-10, 10)*1.5, inches = F, fg = "orange", lwd = 2)

Я проверил некоторые пакеты с функциями для рисования эллипсов (elliplot, ellipse, ellipseplot, carи т.д.), но мне не нравятся их функции. Я не заинтересован в использовании этих пакетов, напротив, я хотел бы написать собственный код.

Моя идея состоит в том, чтобы построить форму, которая лучше всего соответствует реальной фигуре кольца с моими значениями данных четырех радиусов, это может быть эллипс, овал и т. Д.

С кружком я использую только данные одного радио (в моем примере среднее значение всех радиусов). С эллипсом было бы лучше, потому что я могу использовать как минимум два значения, большую ось (A+B) и малую ось (C+D). Но было бы здорово нарисовать фигуру, которая использует значения четырех радиусов (A, B, C, D) или даже больше радиусов.

Здесь парень нарисовал очень хороший суперэллипс, используя R-скрипт, а другой нарисовал несколько эллипсов, как кольца, также в R.

Тем не менее, я не знаю, как использовать их методы для моей конкретной проблемы.

Если у кого-то есть идея, как начать рисовать хотя бы эллипс в R, было бы неплохо. Но было бы здорово узнать, как нарисовать фигуру (овал, эллипс и т. Д.), Используя значения четырех радиусов и, наконец, рассчитать их площадь.

Я был бы очень признателен за вашу помощь или любое направление, чтобы сделать это.

ОБНОВИТЬ:

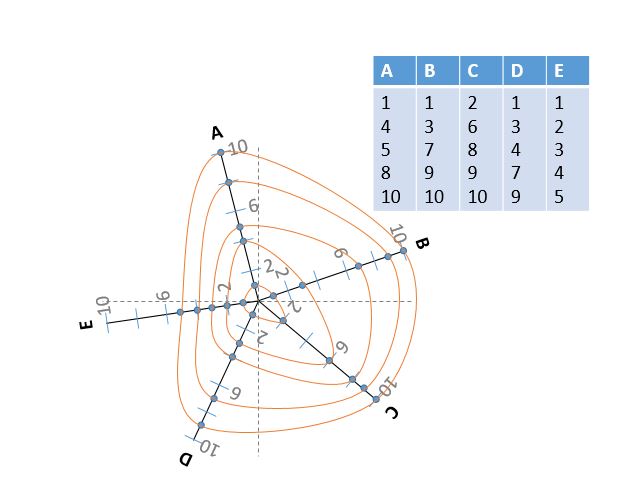
Спасибо @cuttlefish44 за отличный ответ, который был очень полезен для объяснения роста деревьев моим ученикам. Однако большинство тропических деревьев имеют очень неправильные формы, и теперь мне интересно узнать, могу ли я нарисовать эту другую форму с дополнительным радио "Е" и осями радиусов в разных положениях, как эта схема:

любое направление было бы очень полезно для меня.

Answer 1

Если A & B находятся на оси Y, а C & D на оси X, нетрудно вычислить параметры эллипсов. я использовал optim() чтобы получить параметры (Примечание: этот подход имеет крошечную ошибку, такую ​​как 2.439826e-12).

манипуляция данными

 # change all data into xy coordinates and make ring-factor
library(reshape2); library(dplyr)

data <- data.frame(
  a = c(1, 4, 5, 8, 10),
  b = c(1, 3, 7, 9, 10) * -1,
  c = c(2, 6, 8, 9, 10) * -1,
  d = c(1, 3, 4, 7, 9) )

data <- t(data)
colnames(data) <- LETTERS[1:ncol(data)]   # ring-factor
df <- melt(data, value.name = "x")        # change into long-form

df$y <- df$x                              # make xy coordinates
df[df$Var1=="a"|df$Var1=="b", "x"] <- 0
df[df$Var1=="c"|df$Var1=="d", "y"] <- 0

расчет координат центра, ox & oy

center <- df %>% group_by(Var2) %>% summarize(sum(x)/2, sum(y)/2) %>% as.data.frame()

расчет параметров эллипса; полу-большая и малая ось, ra & rb

opt.f <- function(par, subset, center) {     # target function
  ox <- center[[1]]                          # par[1] and par[2] are ra and rb
  oy <- center[[2]]
  x <- subset$x
  y <- subset$y
  sum(abs((x - ox)^2/par[1]^2 + (y - oy)^2/par[2]^2 - 1))   # from ellipse equation
}

lev <- levels(df$Var2)

## search parameters
res <- sapply(1:length(lev), function(a) 
  optim(c(1,1), opt.f, subset = subset(df, Var2 == lev[a]), 
        center = center[a, 2:3], control = list(reltol = 1.0e-12)))

res  # result. you can get detail by res[,1etc]. values are not 0 but much nearly 0

функция для построения графика (возможно, некоторые пакеты имеют похожий)

radian <- function(degree) degree/180*pi
plot.ellipse <- function(ox, oy, ra, rb, phi=0, start=0, end=360, length=100, func=lines, ...) {
  theta <- c(seq(radian(start), radian(end), length=length), radian(end))
  if (phi == 0) {
    func(ra*cos(theta)+ox, rb*sin(theta)+oy, ...)
  } else {
    x <- ra*cos(theta)
    y <- rb*sin(theta)
    phi <- radian(phi)
    cosine <- cos(phi)
    sine <- sin(phi)
    func(cosine*x-sine*y+ox, sine*x+cosine*y+oy, ...)
  }
}

рисовать

plot(0, type="n", xlim=c(-10, 10), ylim =c(-10, 10), asp=1, xlab="x", ylab="y", axes = F)
axis(1, pos=0);axis(2, pos=0, las=2)
points(df$x, df$y)
for(a in 1:length(lev)) plot.ellipse(ox = center[a, 2], oy = center[a, 3], 
                                     ra = res[,a]$par[1], rb = res[,a]$par[2], length=300)

area <- sapply(res[1,], function(a) pi * a[1] * a[2])