Логика высказываний и доказательства

Question

Я пытаюсь доказать приведенный ниже случай для домашнего задания, и я работал над ним часами, но все же не повезло.

r) -> p -> q -> r">

Любые предложения или комментарии относительно того, что я делаю неправильно?

Answer 1

Вот как вы можете доказать это в Coq:

Coq < Theorem curry : forall p q r, ((q /\ p) -> r) -> p -> q -> r.
1 subgoal

  ============================
   forall (p q : Prop) (r : Type), (q /\ p -> r) -> p -> q -> r

Сначала назовем все помещения:

curry < intros p q r f x y.
1 subgoal

  p : Prop
  q : Prop
  r : Type
  f : q /\ p -> r
  x : p
  y : q
  ============================
   r

Единственная предпосылка, которая производит подцель r является f:

curry < apply f.
1 subgoal

  p : Prop
  q : Prop
  r : Type
  f : q /\ p -> r
  x : p
  y : q
  ============================
   q /\ p

Применять f сначала нам нужно удовлетворить подзадачи q а также p:

curry < split.
2 subgoals

  p : Prop
  q : Prop
  r : Type
  f : q /\ p -> r
  x : p
  y : q
  ============================
   q

subgoal 2 is:
 p

Помещение y является доказательством подцели q:

curry < exact y.
1 subgoal

  p : Prop
  q : Prop
  r : Type
  f : q /\ p -> r
  x : p
  y : q
  ============================
   p

Помещение x является доказательством подцели p:

curry < exact x.
No more subgoals.

Были сделаны. Вот полное доказательство:

curry < Qed.
intros p q r f x y.
apply f.
split.
 exact y.

 exact x.

curry is defined

В языках функционального программирования, таких как Haskell, вы должны иметь:

curry :: ((q, p) -> r) -> p -> q -> r
curry f x y = f (y, x)

Все работает благодаря переписке Карри-Ховарда.

Answer 2

Благодаря @Aadit у нас есть доказательства Coq, и было бы справедливо - этично? - представить доказательство Agda.

Непосредственное и простое доказательство

open import Data.Product

portation : {P Q R : Set} → (P × Q → R) → (P → Q → R)
portation P×Q→R = λ p q → P×Q→R (p , q)

Конечно, это может быть не совсем понятно, если спрашивающий не знаком с Агдой и ищет формализацию. Итак, давайте добавим некоторые детали!

В конструктивной логике высказывания можно рассматривать как маленькие типы:

ℙrop = Set

Тогда спаривание является обычным способом формирования сопряжения,

data _∧_ (P Q : ℙrop) : Set where
 ∧I : P → Q → P ∧ Q

В конструктивной логике импликация - это просто функциональное пространство: сказать, что одно подразумевает другое, равносильно получению процедуры, которая при вводе первого вида возвращает результат второго типа.

_⇒_ : (P Q : ℙrop) → Set
_⇒_ = λ P Q → (P → Q)

В этом случае введение импликации - это просто обычное определение функции, а устранение импликации - не что иное, как применение функции.

⇒I : ∀ {P Q} → (P → Q) → P ⇒ Q
⇒I P→Q = P→Q

⇒E : ∀ {P Q} → P ⇒ Q → P → Q
⇒E P→Q p = P→Q p

Теперь спрашивающий использует стиль доказательств с естественным выводом, поэтому давайте введем некоторый синтаксический сахар, чтобы преодолеть разрыв от бумажных и карандашных доказательств до формализации Агды.

syntax ⇒I {P} {Q} (λ p → q) = ⇒-I-assuming-proof p of P we-have Q proved-by q

Теперь доказательство!

shunting : (P Q R : ℙrop) → (P ∧ Q) ⇒ R → P ⇒ (Q ⇒ R)
shunting P Q R P∧Q⇒R =
                    ⇒-I-assuming-proof p of P
                    we-have Q ⇒ R proved-by

                        ⇒-I-assuming-proof q of Q
                        we-have R proved-by

                            ⇒E P∧Q⇒R (∧I p q)

Что не только вполне читабельно, но и несколько близко к презентации аскера!

Агда такая радость!

Answer 3

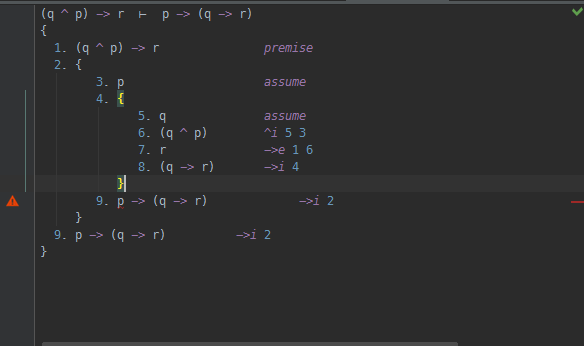
Это доказательство с использованием средства проверки естественных вычетов в стиле Flement от Klement и учебника forallx, дающего пояснения. (Ссылки ниже.)

Основная проблема с первоначальной попыткой состоит в том, что строки 8 и 9 не выполнили предположения. Похоже, что они оставались в тех же подпунктах, основанных на отступах и скобках.

В противном случае доказательство будет таким же, как я предоставил. В моей строке 6 я выполнил предположение, которое я сделал из "Q" в строке 3, введя условное (строки 3-5). В моей строке 7 я выполнил предположение "P", сделанное в строке 2, введя условное (строки 2-6).

---

Ссылка

Редактор и средство проверки естественных дедукций Кевина Клемента в стиле JavaScript/PHP Fitch http://proofs.openlogicproject.org/

П.Д. Магнус, Тим Баттон с дополнениями Дж. Роберта Лофтиса, ремикс и рецензия Аарона Томаса-Болдука, Ричарда Зака, forallx Калгари Ремикс: Введение в формальную логику, зима 2018. http://forallx.openlogicproject.org/