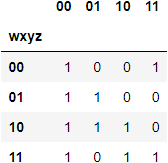Доказательство неоптимальности карты Карно

Question

Я был бы признателен за помощь в поиске литературы, посвященной оптимальности K-карт.

Я понимаю, как, например, вы можете отображать между выражениями SOP (сумма-продукта) и K-картой, и почему в целом вы ожидаете, что оптимизированное выражение K-карты будет проще, так как нахождение максимальной группировки 1 соответствует обнаружению некоторых избыточностей в простом выражении СОП.

Я смутно вижу, что метод K-отображения может не дать оптимальных решений, потому что кажется, что единственное, что мы на самом деле делаем, - это использование преимуществ дистрибутивных и тождественных (A + A' = 1) свойств булевой алгебры. Но я не совсем понимаю, какие алгебраические операции мы не выполняем с K-картой, что может позволить нам найти более оптимальное решение.

В результате я не знаю, как начать доказательство того, что K-карты не всегда оптимальны.

Я пытался прочитать: это, но в этой статье только что процитировано, что проблема поиска оптимального булева выражения находится в NP, и я думаю, что автор просто неявно говорит, что K-карты не могут быть оптимальными, поскольку в качестве алгоритма они не бегут во время NP.

Почему K-карты неоптимальны, а не просто в "контрпримере", на самом деле, почему? Вы можете доказать это мне или направить меня к доказательству?

Answer 1

Что вы считаете оптимальным? K-карта дает оптимальные уравнения только в форме SOP или POS. Так что это зависит от того, что вы хотите.

Алгебраические операции, которые не выполняются, включают, например, Distributivity of ∧ over ∨, Применение этого правила может дать вам функцию с меньшим количеством терминов.

K-карта не даст вам уравнения, используя то есть xor, поскольку в полученных уравнениях используются только or а также and а также not, Итак, если я возьму таблицу истинности, полученную из функции (с ^ являющийся xor):

lambda a, b, c, d: a ^ b ^ c ^ d

итоговая таблица истинности не будет иметь прямоугольников, и форму SOP можно считать неоптимальной:

lambda a, b, c, d: (not a and b and c and d) or (not a and not b and not c and d) or (not a and not b and c and not d) or (not a and b and not c and not d) or (a and b and c and not d) or (a and b and not c and d) or (a and not b and c and d) or (a and not b and not c and not d)

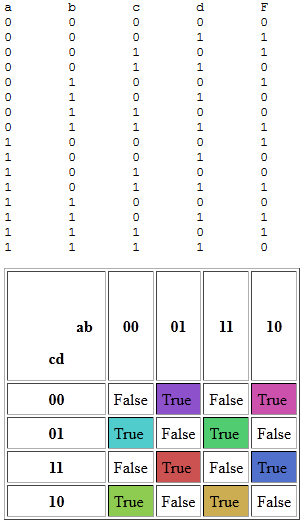
Если вы используете только or а также and и ваша функция ввода короче, чем ваша функция вывода, вы используете круглые скобки при вводе. Если это так, вы также сможете выделить некоторые переменные в выводе k-карты (используя булеву алгебру), и вы получите уравнение, которое по крайней мере такое же короткое.

Обобщение. Минимизация булевой функции аналогична нахождению уравнения для любой другой серии чисел. Там всегда будет несколько решений. Но какая функция самая простая? Я мог бы сказать: "Дайте мне функцию, которая возвращает 1 для 0, 2 для 1, 4 для 2 и 8 для 3". Вы могли бы сказать, что "функция Pow(2, х)". И я мог бы сказать "неправильно! Я думал о 1 << х". Все значения, где функции не равны, находятся за пределами области спецификации. Они соответствуют "не знает" в K-карте.

Когда я говорю, что "моя функция проще, потому что я просто записываю все термины", вы можете сказать: "Но если я добавлю дополнительную переменную, и она не будет соответствовать вашему шаблону, ваша функция станет слишком громоздкой и сложной, моя просто по-прежнему следует схеме SOP или POS ".

Answer 2

Если это кому-то поможет, я просто попытаюсь описать проблемы, с которыми я столкнулся с точки зрения оптимальности, когда пытался реализовать K-map в python. Вот жадный алгоритм, который я использовал для логической функции с 4 переменными в форме SOP:

1. Сначала проверьте все minterms только с одной переменной (например, xили же ¬x) и выберите уникальные, которые охватывают подмножество только в функции
2. Затем проверьте все минтермы с двумя переменными (например, xyили же ¬wz) и выберите уникальные, которые охватывают подмножество тех, которые еще предстоит охватить в функции.
3. Затем проверьте все minterms с тремя переменными (например, xyzили же ¬wxy) и выберите уникальные, которые охватывают подмножество тех, которые еще предстоит охватить в функции.
4. Наконец, добавьте остальные минтермы с 4 переменными, соответствующие тем, которые остались незакрытыми, если таковые имеются.

Теперь рассмотрим функцию f(w,x,y,z)=∑(0,2,4,5,8,10,11,12,13,15)как показано ниже:

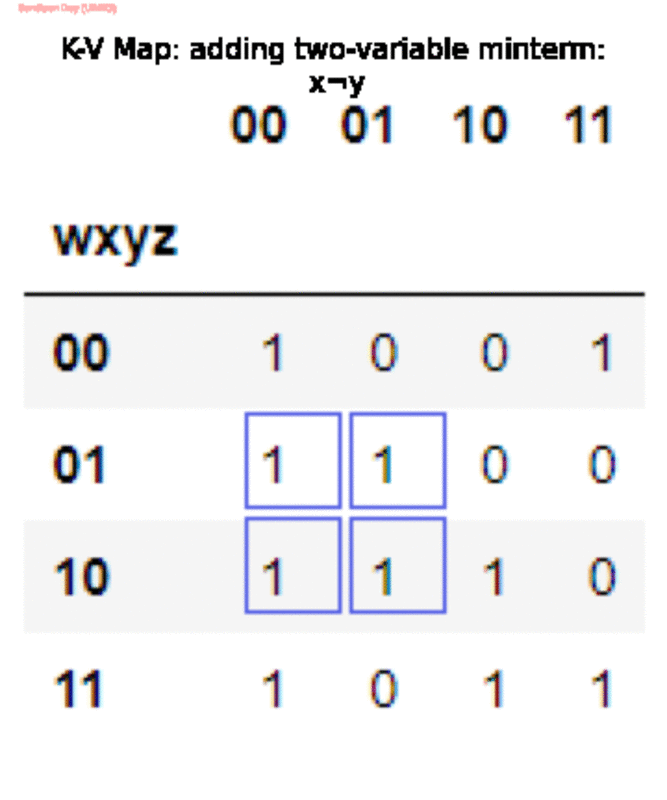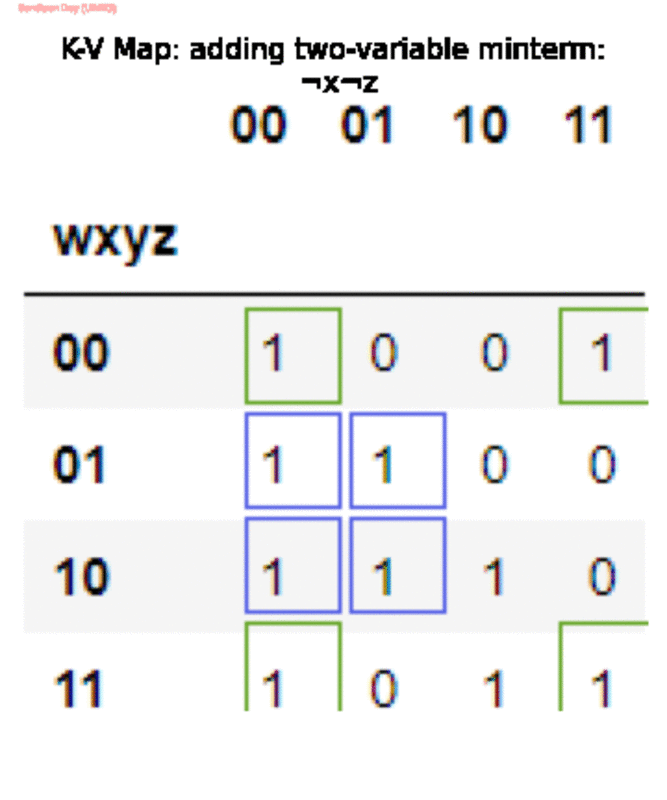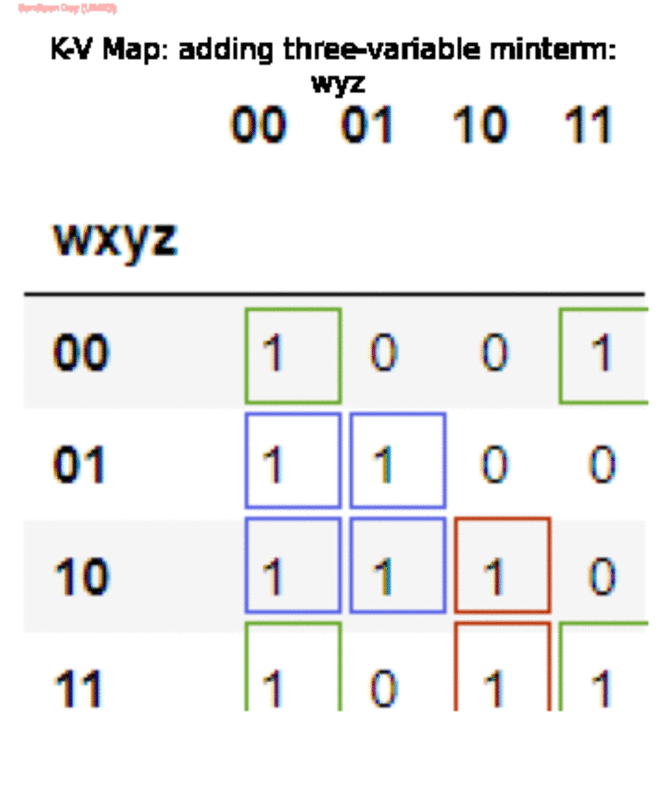
Используя описанные выше шаги, я сначала застрял на следующем локальном минимуме, который определенно был минимальным представлением SOP, но не минимальным представлением: f(w,x,y,z) = x¬y + ¬x¬z + w¬xy + wxz. Для представления f потребовалось 4 минтерма, что неоптимально. Критическая ошибка алгоритма заключалась в том, что он выбрал пару минтермов с тремя переменными и wxz, когда одного () было бы достаточно, так как он проверял минтермы в определенном порядке и выбирал тот, который имел некоторое совпадение с еще не охваченными. Как только он выбрал w¬xy, ему, должно быть, пришлось выбрать другой минтерм, так как он все еще не был покрыт.

Теперь, если вместо этого на самом шаге алгоритм использует порядок minterms с 3 переменными, который учитывает wyzперед рассмотрением двух других он выведет оптимальную SOP: f(wxyz) = x¬y + ¬x¬z + wyz, как показано ниже.