Сравните вариограмму и функцию вариограммы

Question

Я предположил (вероятно, ошибочно), что в самых простых случаях вывод variog в geoR пакет и variogram в sp пакет был бы таким же.

У меня есть этот набор данных:

head(final)
lat     lon  elev seadist  tradist samples rssi
1 60.1577 24.9111 2.392     125 15.21606     200  -58
2 60.1557 24.9214 3.195     116 15.81549     200  -55
3 60.1653 24.9221 4.604     387 15.72119     200  -70
4 60.1667 24.9165 7.355     205 15.39796     200  -62
5 60.1637 24.9166 3.648     252 15.43457     200  -73
6 60.1530 24.9258 2.733      65 16.10631     200  -57

это сделано (я предполагаю) непроецированных данных, поэтому я проецирую их

#data projection
#convert to sp object:
coordinates(final) <- ~ lon + lat #longitude first
library(rgdal)
proj4string(final) =  "+proj=longlat +datum=WGS84"
UTM <- spTransform(final, CRS=CRS("+proj=utm +zone=35V+north+ellps=WGS84+datum=WGS84"))

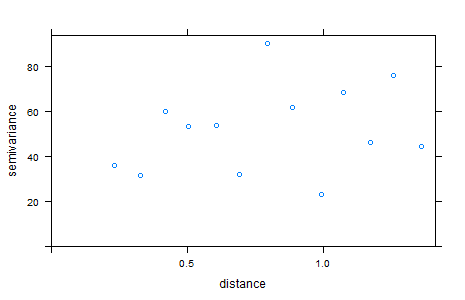
и производить вариограмму без тренда в соответствии с gstat библиотека

var.notrend.sp<-variogram(rssi~1, UTM)
plot(var.notrend.sp)

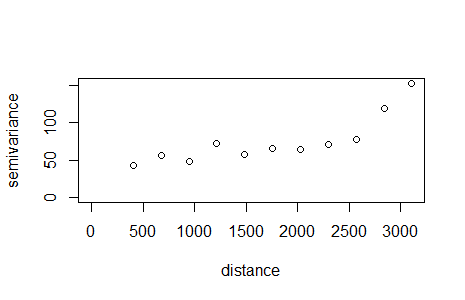
пытаясь получить тот же результат в geoR Я иду с

UTM1<-as.data.frame(UTM)
UTM1<-cbind(UTM1[,6:7], UTM1[,1:5])
UTM1
coords<-UTM1[,1:2]
coords
var.notrend.geoR <- variog(coords=coords, data=rssi,estimator.type='classical')
plot(var.notrend.geoR)

Answer 1

Пара моментов.

• gstat может работать с непроецированными данными, и вычислит расстояние большого круга
• установка "проекции", чтобы быть "+proj=longlat +datum=WGS84" не преобразует данные в декартову сеточную систему (такую ​​как UTM)

Что вы видите на выходе variogram тот факт, что (разумно) использует большие расстояния круга. Если вы посмотрите на масштаб оси расстояний, вы увидите, что диапазоны довольно разные, потому что geoR не знает (и не может объяснить) тот факт, что вы не используете проекцию на основе сетки.

Если вы хотите сравнить яблоки с яблоками, используйте rgdal а также spTransform преобразовать систему координат в соответствующую проекцию, а затем создать вариограммы с аналогичными характеристиками. (Обратите внимание, что gstat определяет срез (длина диагонали прямоугольника, охватывающего данные, делится на три.)).

Эмпирическая вариограмма сильно зависит от определения расстояния и выбора биннинга. (см. блестящую основанную на модели геостатистику Диггла и Рибейро, особенно главу 5, которая подробно рассматривает эту проблему.