Метод квадратурного численного интегрирования Тань-синь, сходящийся к неправильному значению
Я пытаюсь написать программу на Python, чтобы использовать квадратурную Tanh-sinh для вычисления значения:
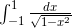
но хотя программа сходится к разумному значению без ошибок в каждом случае, она не сходится к правильному значению (которое является пи для данного конкретного интеграла), и я не могу найти проблему.
Вместо того, чтобы запрашивать желаемый уровень точности, программа запрашивает количество требуемых оценок функций, чтобы упростить сравнение сходимости с более простыми методами интеграции. Число оценок должно быть нечетным числом, поскольку используемое приближение

Кто-нибудь может подсказать, что я мог сделать не так?
import math
def func(x):
# Function to be integrated, with singular points set = 0
if x == 1 or x == -1 :
return 0
else:
return 1 / math.sqrt(1 - x ** 2)
# Input number of evaluations
N = input("Please enter number of evaluations \n")
if N % 2 == 0:
print "The number of evaluations must be odd"
else:
print "N =", N
# Set step size
h = 2.0 / (N - 1)
print "h =", h
# k ranges from -(N-1)/2 to +(N-1)/2
k = -1 * ((N - 1) / 2.0)
k_max = ((N - 1) / 2.0)
sum = 0
# Loop across integration interval
while k < k_max + 1:
# Compute abscissa
x_k = math.tanh(math.pi * 0.5 * math.sinh(k * h))
# Compute weight
numerator = 0.5 * h * math.pi * math.cosh(k * h)
denominator = math.pow(math.cosh(0.5 * math.pi * math.sinh(k * h)),2)
w_k = numerator / denominator
sum += w_k * func(x_k)
k += 1
print "Integral =", sum
4 ответа
Для чего это стоит, у Сципи есть функции численного интегрирования
Например,
from scipy import integrate
check = integrate.quad(lambda x: 1 / math.sqrt(1 - x ** 2), -1, 1)
print 'Scipy quad integral = ', check
дает результат
Четырехугольный интеграл Сципи = (3.141592653589591, 6.200897573194197e-10)
где второе число в кортеже является абсолютной ошибкой.
Тем не менее, я смог заставить вашу программу работать с некоторой настройкой (хотя это только первоначальная попытка):
1) Установите размер шага h равным 0,0002 (примерно 1/2^12), как предлагается в этой статье.
Но обратите внимание - в документе фактически предлагается итеративное изменение размера шага - с фиксированным размером шага вы достигнете точки, в которой синус или кошка станут слишком большими для достаточно больших значений kh. Вероятно, было бы лучше попытаться реализовать на основе подхода этой статьи.
Но придерживаясь данного вопроса,
2) Убедитесь, что вы установили достаточно итераций, чтобы интеграция действительно сходилась, т.е. достаточно итераций, чтобы math.fabs(w_k * func(x_k)) < 1.0e-9
Благодаря этим настройкам я смог добиться того, чтобы интеграция сходилась к правильному значению числа пи до 4 значащих цифр, используя> 30000 итераций.
Например, с 31111 итерациями вычисленное значение пи было 3,14159256208.
Пример кода с изменениями (заметьте, я заменил сумму на сумму, сумма - это имя встроенной функции Python):
import math
def func(x):
# Function to be integrated, with singular points set = 0
if x == 1 or x == -1 :
return 0
else:
return 1 / math.sqrt(1 - x ** 2)
# Input number of evaluations
N = input("Please enter number of evaluations \n")
if N % 2 == 0:
print "The number of evaluations must be odd"
else:
print "N =", N
# Set step size
#h = 2.0 / (N - 1)
h=0.0002 #(1/2^12)
print "h =", h
# k ranges from -(N-1)/2 to +(N-1)/2
k = -1 * ((N - 1) / 2.0)
k_max = ((N - 1) / 2.0)
thesum = 0
# Loop across integration interval
actual_iter =0
while k < k_max + 1:
# Compute abscissa
x_k = math.tanh(math.pi * 0.5 * math.sinh(k * h))
# Compute weight
numerator = 0.5 * h * math.pi * math.cosh(k * h)
dcosh = math.cosh(0.5 * math.pi * math.sinh(k * h))
denominator = dcosh*dcosh
#denominator = math.pow(math.cosh(0.5 * math.pi * math.sinh(k * h)),2)
w_k = numerator / denominator
thesum += w_k * func(x_k)
myepsilon = math.fabs(w_k * func(x_k))
if actual_iter%2000 ==0 and actual_iter > k_max/2:
print "Iteration = %d , myepsilon = %g"%(actual_iter,myepsilon)
k += 1
actual_iter += 1
print 'Actual iterations = ',actual_iter
print "Integral =", thesum
Использование библиотеки мультиточности mpmath:
from mpmath import *
mp.dps = 100
h = mpf(2**-12);
def weights(k):
num = mpf(0.5)*h*pi*cosh(k*h)
den = cosh(mpf(0.5)*pi*sinh(k*h))**2
return (num/den)
def abscissas(k):
return tanh(mpf(0.5)*pi*sinh(k*h))
def f(x):
return 1/sqrt(1 - mpf(x)**2)
N = 20000
result = 0
for k in range(-N, N+1):
result = result + weights(k)*f(abscissas(k))
print result - pi
дает за ошибку
-3.751800610920472803216259350430460844457732874052618682441090144344372471319795201134275503228835472e-45
Когда дело доходит до квадратуры tanh-sinh, существует множество подводных камней, одна из которых состоит в том, что подынтегральное выражение необходимо оценивать очень близко к границам интервала, на расстояниях, меньших, чем машинная точность, например,1.0 - 1.0e-20в исходном примере. Когда эта точка оценивается, она округляется до1.0 на котором fимеет особенность, и все может случиться. Вот почему вам нужно сначала преобразовать функцию так, чтобы сингулярности были равны 0.
На случай, если 1 / sqrt(1 - x**2), это 1 / numpy.sqrt(-x**2 + 2*x)как для левой, так и для правой особенности. С tanh_sinh ( мой проект) можно получить
import numpy
import tanh_sinh
# def f(x):
# return 1 / numpy.sqrt(1 - x ** 2)
val, error_estimate = tanh_sinh.integrate_lr(
[lambda x: 1 / numpy.sqrt(-x**2 + 2*x)], # = 1 / sqrt(1 - (x-1)**2)
[lambda x: 1 / numpy.sqrt(-x**2 + 2*x)], # = 1 / sqrt(1 - (-(x-1))**2)
2, # length of the interval
1.0e-10
)
print(val, val - numpy.pi)
3.1415926533203944 -2.693987255497632e-10
Я думаю, что часть проблемы может быть связана с диапазоном и размером шага. Я изменил код, чтобы вы могли отдельно указать диапазон и размер шага и переписать некоторые математические выражения. Кажется, дать правильные ответы. Попробуйте, например, 5 и 0,1 в качестве входных данных.
Особой проблемой является расчет math.cosh(0.5 * math.pi * math.sinh(k * h)) как k * h стать большим math.sinh(k * h) растет в геометрической прогрессии, и вычисление математических затрат может быть трудным. импорт математики
def func(x):
# return 1 # very simple test function
# Function to be integrated, with singular points set = 0
if x == 1 or x == -1 :
return 0
else:
return 1 / math.sqrt(1 - x ** 2)
# Input number of evaluations
N = input("Please enter max value for range \n")
print "N =", N
h = input("Please the step size \n")
print "h =", h
k = -N
k_max = N
sum = 0
count = 0
print "k ", k , " " , k_max
# Loop across integration interval
while k < k_max + 1:
# Compute abscissa
v = k
u = math.pi * 0.5 * math.sinh(v)
x_k = math.tanh(u)
#print u
# Compute weight
numerator = 0.5 * math.pi * math.cosh(v)
csh = math.cosh(u)
denominator = csh*csh
w_k = numerator / denominator
print k, v, x_k , w_k
sum += w_k * func(x_k)
count += 1
k += h # note changed
res = sum * h
print "Integral =", sum * h
Вы должны понимать, что +1 и -1 являются особыми точками вашей подынтегральной функции, f(x)-->+infinity как x-->+1,-1, Таким образом, вы можете использовать свою любимую квадратурную формулу вдали от граничных точек, но вы должны разработать специальную квадратурную форму, основанную на локальном расширении f(x) по соседству с ними.
Эскиз подхода:
Выберите немного
epsilon<<1,Разложить интеграл
Iна гладкие и особые части:I_smoothявляется неотъемлемой частью[-1+epsilon, 1-epsilon]I_singularявляются интегралами от[-1, -1+epsilon]а также[1-epsilon, 1],
Примените свое стандартное квадратурное правило внутри интервала
[-1+epsilon, 1-epsilon]получитьI_smooth,Выполните локальное разложение вокруг особых точек (например, x = 1):
f(x) = 1/sqrt(1-x) * (a0 + a1*(1-x) + a2*(1-x)^2 + ...) = f0(x-1) + f1(x-1) + f2(x-1) + ..который просто расширение Тейлора о
x=1изf(x)*sqrt(1-x)умножается на1/sqrt(1-x), (К сожалению, вам нужно немного поработать над математикой и разработать расширение Тейлора, если у вас нет Mathematica или вы не найдете его где-нибудь в виде таблицы.)Каждый термин
fn(x-1) = an*(1-x)^n/sqrt(1-x) может быть интегрирован точно (это просто функция мощности). ПозволятьFnбыть неотъемлемой частьюfnот1-epsilonв1, приближенныйI_singular = F0 + F1 + F2 + ...до заказа, который вы хотите.В заключение:
I = I_smooth + I_singular
Примечание: для повышения точности вы не должны делать epsilon слишком мал, потому что разрушение интеграла делает задачу численно плохо обусловленной, а скорее увеличивает порядок разложения Тейлора.