Математика: когда мы используем логарифмы и как это работает?

Question

Я решал:

Мы знаем содержание испарителя (содержание в мл), процент пены или газа, потерянного каждый день (evap_per_day) и порог (порог) в процентах, после которого испаритель больше не используется. Все цифры строго положительные. Программа сообщает n-й день (целое число), в которое испаритель не будет использоваться.

Мое решение с рекурсией:

if (content > (initialContent / 100) * threshold) {
   double postContent = content - (content / 100) * evap_per_day;
   iterations++;
   return recursiveEvaporator(postContent, evap_per_day, threshold, initialContent, iterations);
}

Но потом я нашел более изощренное решение:return (int)Math.ceil(Math.log(threshold / 100.0) / Math.log(1.0 - evap_per_day / 100.0)); Не могли бы вы объяснить, как здесь работают логарифмы и почему мы выбираем натуральный логарифм?

Answer 1

• Прежде всего, вы должны получить четкое изображение eэто основание натурального логарифма. e - константа, представляющая приближение (1 + 1/n)^n что мы призываем, когда говорим о постоянном росте
  

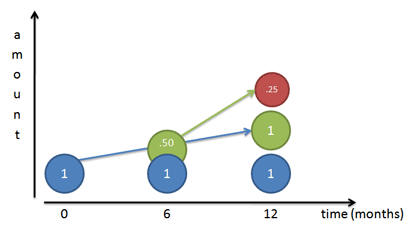
  Мы видим, что вновь появившееся "дополнение" участвовало в дальнейшем возведении в степень. Грубо говоря: e^x - наш доход после x, где x -t*r (t-time; r-rate)

  • ln(y) - обратная операция, мы стремимся узнать, сколько времени нужно потратить на ожидание y дохода.

    ---

Возвращая предмет вашего вопроса ln(threshold) - это t * r (время * скорость) ln(1 - evap_per_day) - это на * r, чтобы вывести 90%! но не начальное, опять же нам нужно ln потому что 90% постоянно уменьшается, и мы должны учитывать это. Мы делим произведение ln(порог) на ln(1 - evap_per_day), чтобы узнать время.

Итак, правильное решение: (int)Math.ceil(Math.log(threshold / 100.0) / (ln(1.0 - evap_per_day / 100.0))

Answer 2

Это случай использования экспоненциального убывания и решения для времени

Формула экспоненциального распада: A = A_o(1 - r)^t, где A - конечная величина, A_o - начальная величина, r - скорость распада, а t - время. Для этого вопроса мы хотим знать количество дней до тех пор, пока начальное количество не станет равным или ниже порогового процента от начального количества, испаряясь с определенным процентом в день. Мы можем переписать уравнение следующим образом: (используя значения в процентах для порогового значения и параметра "ЭксПерДень", чтобы упростить объяснение) А_о (порог) = А_о (1 - ЭППЕРДЕЙ) ^ t

упрощается до: threshold = (1 - empPerDay)^t

теперь мы используем журналы для решения t

журнал (порог) = журнал ((1- EpPerDay)^t)

используйте один из законов бревен, чтобы переместить t

журнал (порог) = t(журнал (1-испарительДень))

решить для t

журнал (порог)/ журнал (1-испарительДень) = t

Используйте потолок, чтобы округлить.