Как реализовать интерполяционную линию задержки и весь проходной фильтр с помощью сильного алгоритма karplus?

Question

Хорошо, я реализовал сильный алгоритм karplus в C. Это простой алгоритм для имитации звука оторванной струны. Вы начинаете с кольцевого буфера длины n (n = частота дискретизации / частота, которую вы хотите), проходите через простой двухточечный средний фильтр y[n] = (x[n] + x[n-1])/2, выведите его, а затем верните обратно в линию задержки. Промыть и повторить. Это сглаживает шум с течением времени, создавая естественный звук струны.

Но я заметил, что при длине линии целочисленной задержки, несколько высоких частот могут быть сопоставлены с одной и той же длиной задержки. Кроме того, длина целочисленной задержки не допускает плавно изменяющихся высот (как в вибрато или глиссандо). Я прочитал несколько статей о расширениях алгоритма karplus, и все они говорят об использовании либо интерполированной линии задержки для дробной задержки, либо фильтр всех проходов

http://quod.lib.umich.edu/cgi/p/pod/dod-idx?c=icmc;idno=bbp2372.1997.068
http://www.jaffe.com/Jaffe-Smith-Extensions-CMJ-1983.pdf
http://www.music.mcgill.ca/~gary/courses/projects/618_2009/NickDonaldson/index.html

Я реализовал интерполированные линии задержки раньше, но только в таблицах сигналов, где буфер сигнала не изменяется. Я просто шаг за шагом по разным ставкам. Но что меня смущает, так это то, что когда речь заходит об алгоритме KS, статьи, похоже, говорят о фактическом изменении длины задержки, а не просто о скорости, которую я прохожу. Алгоритм ks усложняет ситуацию, потому что я должен постоянно возвращать значения обратно в линию задержки.

Итак, как бы я пошел на реализацию этого? Вернуть ли интерполированное значение обратно или как? Полностью ли я избавился от двухточечного усредняющего фильтра низких частот?

И как будет работать весь проходной фильтр? Должен ли я заменить фильтр усреднения по 2 точкам на фильтр всех проходов? Как бы я скользил между отдаленными высотами с глиссандо, используя метод линейной интерполяции или метод Allpass Filter?

Answer 1

Алгоритмы цифровой обработки сигналов часто представляются в виде блок-схем по понятной причине - это отличный способ думать о них. При их кодировании думайте о каждом блоке как об отдельном блоке с фиксированными входами и выходами. Я думаю, что некоторые из ваших вопросов возникли из-за попыток преждевременно объединить различные элементы системы.

Вот блок-схема для Karplus Strong.

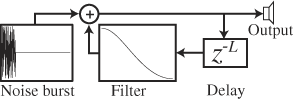
Для блока задержки вам нужно реализовать дробную линию задержки. Это будет включать в себя собственный фильтр нижних частот, но это деталь того, как реализована линия задержки. Для эффекта Karplus Strong также требуется фильтр нижних частот. Характеристики этих фильтров будут разными. Не пытайтесь комбинировать. Кстати, выбранный вами усредняющий фильтр нижних частот имеет плохую частотную характеристику, которая вводит эффект "гребенчатого фильтра". Возможно, вы захотите разработать более сложный FIR или IIR фильтр.

Итак, как бы я пошел на реализацию этого? Вернуть ли интерполированное значение обратно или как? Полностью ли я избавился от двухточечного усредняющего фильтра низких частот?

Вы подаете интерполированную, суммированную выборку обратно в линию задержки, как показано на блок-схеме. В некоторых случаях это может привести к увеличению чистого усиления системы, и вам может потребоваться "нормализовать" вывод задержки, чтобы она не вышла из-под контроля, если вас это беспокоит.

Как вы упомянули, существует много правильных стратегий для реализации линии дробной задержки, включая интерполяцию и фильтрацию всех каналов. Идея в том, что вы хотите сохранить read а также write индексы в линии задержки. Длина строки задержки - это не общая длина буфера памяти, а разница между индексами по модулю общей длины линии задержки. Сделайте линию задержки настолько большой, насколько это необходимо, и не беспокойтесь о ее изменении.

Я считаю, что наиболее удобно рассматривать чтение и запись как свободные счетчики, которые никогда не оборачиваются и не устаревают, потому что тогда

current_delay_length = (write - read) % total_delay_length
current_read_sample = delay_line[read % total_delay_length]

где % это модуль. Счетчики записи и чтения также могут содержать дробную длину, если они являются значениями с плавающей запятой или установлены как фиксированная точка. В любом случае это позволяет легко изменять длину линии задержки. Важно обеспечить соблюдение минимальной задержки (запись> чтение).

Хотите верьте, хотите нет, но вы измените длину линии задержки, изменив частоту ее прохождения, точно так же, как буфер с фиксированной длиной. Обычно вы немного модулируете индекс чтения. Он никогда не должен отставать от указателя записи больше, чем на длину буфера, или опережать его, иначе вы получите затруднения. Но вы можете свободно перемещать указатель чтения в любом месте после указателя записи. Изменение модуляции приведет к различным эффектам.

Я подчеркиваю, что такие эффекты, как glissando, проистекают из того, как обрабатываются индексы чтения и записи в строке задержки, а не как это реализовано. Вы получите аналогичные звуки из универсального фильтра или линейно интерполированной линии задержки. Лучшие линии с дробной задержкой уменьшают шум псевдонимов и поддерживают, например, более быстрые изменения указателя чтения.

Answer 2

Я реализовал три варианта, у всех есть свои плюсы и минусы, но ни один не идеален, как мне хотелось бы. Может быть, кто-то имеет лучшие алгоритмы и хочет поделиться этим здесь?

В общем, я делаю это так, как описывает jbarlow. Я использую кольцевой буфер длиной 2^x, где x "достаточно большой", например, 12, что будет означать максимальную длину задержки 2^12=4096 выборок, это ~12 Гц как самая низкая базовая частота, если рендеринг @ 48 кГц, Причиной степени двойки является то, что по модулю можно выполнять побитовое И, что намного дешевле, чем фактическое по модулю.

// init
int writepointer = 0;

// loop:
writepointer = (writepointer+1) & 0xFFF;

Указатель записи остается простым и начинается, например, с 0 и всегда увеличивается на 1 для каждой выходной выборки.

Указатель чтения начинается с дельты относительно указателя записи, вычисляемой заново каждый раз, когда частота должна измениться.

// init
float delta = samplingrate/frequency;
int readpointer = (writepointer-(int)delta)-1) & 0xFFF;
float frac = delta-(int)delta;
weight_a = frac;
weight_b = (1.0-frac);

// loop:
readpointer = (readpointer + 1) & 0xFFF;

Он также увеличивается на 1, но обычно лежит более или менее между двумя целочисленными позициями. Мы используем округленную вниз позицию для хранения в целочисленном readpointer. Вес между этим и следующими образцами составляет weight_a и _b.

Вариация # 1: игнорировать дробную часть и указывать (целочисленный) указатель чтения как есть.

Плюсы: без побочных эффектов, идеальная задержка (нет неявного низкого прохода из-за задержки, означает полный контроль над частотной характеристикой, без артефактов)

Минусы: базовая частота в основном слегка смещена, квантована в целочисленные позиции. Это звучит очень расстроено для нот с высоким тоном и не может вносить изменения тонкого тона.

Вариация № 2: Линейная интерполяция между выборкой readpointer и следующей выборкой. Означает, что я на самом деле считываю два последовательных сэмпла из кольцевого буфера и суммирую их, взвешенные на weight_a и weight_b соответственно.

Плюсы: идеальная базовая частота, без артефактов

Минусы: линейная интерполяция вводит фильтр нижних частот, который может быть нежелателен. Еще хуже, низкие частоты варьируются в зависимости от поля. Если дробная часть оказывается близкой к 0 или 1, происходит лишь небольшое количество фильтрации нижних частот, в то время как дробная часть, составляющая около 0,5, выполняет тяжелую фильтрацию нижних частот. Это делает некоторые ноты инструмента более яркими, чем другие, и никогда не может быть ярче, чем позволяет этот низкочастотный диапазон. (плохо для стальной гитары или клавесина)

Вариация № 3: Вид дрожания. Я всегда читаю задержку из целочисленной позиции, но отслеживаю ошибку, которую я делаю, значит, есть переменная, которая суммирует дробную часть. Когда оно превышает 1, я вычитаю 1.0 из ошибки и считываю задержку из второй позиции.

Плюсы: безупречная базовая частота, без скрытых низких частот

Минусы: вводит слышимые артефакты, которые заставляют его звучать с низким качеством звука. (как пониженная выборка с ближайшим соседом).

Вывод: ни один из вариантов не удовлетворяет. Либо у вас не может быть правильной высоты тона, нейтральной частотной характеристики или вы вводите артефакты.

Я читал в литературе, что все-проходной фильтр должен делать это лучше, но разве линия задержки уже не является? Какая будет разница в реализации?