Построение DFA в алгоритме Кнута-Морриса-Пратта

Question

Я имею в виду схему алгоритма Кнута-Морриса-Пратта (KMP) для поиска подстрок в книге Седжвика "Алгоритмы" (4-е изд.).

Алгоритм KMP использует резервную копию в поиске подстроки на основе детерминированного конечного автомата (DFA). Я понимаю, как DFA входит в алгоритм, однако я не понимаю, как создать DFA, что делается с помощью следующего фрагмента кода:

dfa[pat.charAt(0)][0] = 1;
for (int X = 0; j = 1; j< M; j++) {
    for (int c = 0; c < R; c++) {
       dfa[c][j] = dfa[c][X];
    }
    dfa[pat.charAt(j)][j] = j+1;
    X = dfa[pat.charAt(j)][X];
}

где M длина шаблона pat а также R размер алфавита. charAt() Функция возвращает целочисленное значение символа в соответствующей позиции.

Может кто-нибудь объяснить, каким образом этот кусок кода создает dfa? Я потерян в действительном интуитивном значении внутреннего цикла for.

Answer 1

Давайте посмотрим на следующую FA для шаблона ACACAGA.

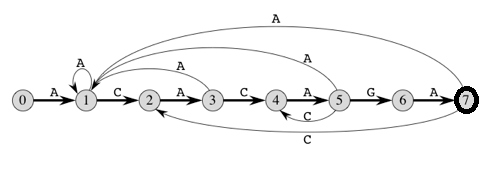
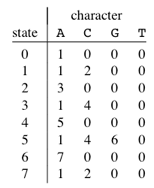
Приведенные выше диаграммы представляют графическое и табличное представление шаблона ACACAGA.

Здесь число состояний в DFA равно M + 1, где M - длина шаблона. Главное, чтобы построить DFA, это получить следующее состояние из текущего состояния для каждого возможного символа. Учитывая символ x и состояние k, мы можем получить следующее состояние, рассматривая строку "pat[0..k-1]x", которая в основном является конкатенацией символов шаблона pat [0], pat 1 … pat [k- 1] и символ х. Идея состоит в том, чтобы получить длину самого длинного префикса данного шаблона таким образом, чтобы префикс также был суффиксом (LPS) "pat[0..k-1]x". Значение длины дает нам следующее состояние.

Например, давайте посмотрим, как получить следующее состояние из текущего состояния 5 и символа "C" на диаграмме выше. Нам нужно рассмотреть строку "pat[0..5]C", которая является "ACACAC". Длина самого длинного префикса шаблона, так что префикс является суффиксом "ACACAC", равен 4 ("ACAC"). Таким образом, следующее состояние (из состояния 5) - 4 для символа "C".

// dfa[i][j] = k denotes the transition function will go k'th state 
// with character i from state j

// DFA will go always (i + 1)'th state from i'th state 
//if the character c is equal to current character of pattern 
dfa[pat.charAt(0)][0] = 1;

//  here X is initialized with LPS (longest prefix suffix) 
// of pattern[0....j - 1]. LPS[0] is always 0
for (int X = 0; j = 1; j< M; j++) {
    for (int c = 0; c < R; c++) { // for all possible characters
        // transition function from j'th state taking character c 
        // will go to the same state where it went from X(LPS)'th state
        // taking character c (justify it with an example) 
        dfa[c][j] = dfa[c][X];
    }
    // DFA will go always (i + 1)th state from i'th state if 
    // the character c is equal to current character of pattern
    dfa[pat.charAt(j)][j] = j + 1;
    X = dfa[pat.charAt(j)][X]; // update LPS
}