Mathematica RegionPlot на поверхности единичной сферы?

Question

Я использую RegionPlot3D в Mathematica, чтобы визуализировать некоторые неравенства. Поскольку неравенства однородны по координатам, они однозначно определяются их пересечением с единичной сферой. Это дает некоторые двумерные области на поверхности сферы, которые я хотел бы построить. У меня вопрос как?

Если бы меня попросили, я с радостью предоставил бы код Mathematica; хотя я считаю, что ответ должен быть независимым от деталей регионов, которые я пытаюсь построить.

Заранее спасибо!

Обновление: на случай, если кому-то будет интересно, я недавно закончил работу, в которой использовал ответ Саши ниже, чтобы составить несколько сюжетов. Статья посвящена основам симметричной М-теории и была опубликована на прошлой неделе. Он содержит графики, такие как этот:

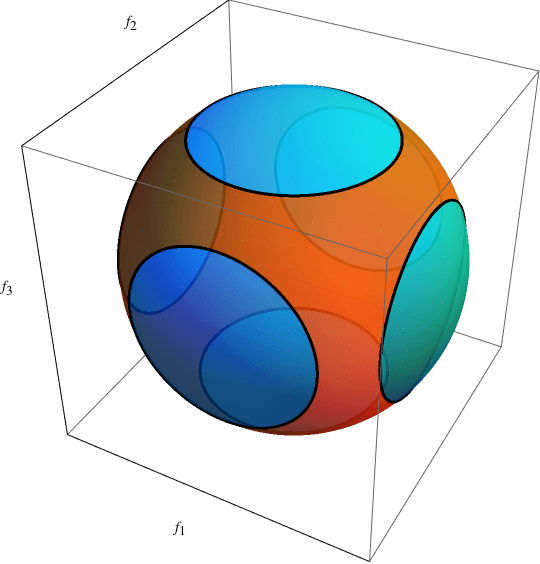
Еще раз спасибо!

Answer 1

Пожалуйста, посмотрите в RegionFunction, Вы можете использовать свое неравенство дословно в нем внутри ParametricPlot3D,

Show[{ParametricPlot3D[{Sin[th] Cos[ph], Sin[th] Sin[ph], 
    Cos[th]}, {th, 0, Pi}, {ph, 0, 2 Pi}, 
   RegionFunction -> 
    Function[{x, y, z}, And[x^3 < x y z + z^3, y^2 z < y^3 + x z^2]], 
   PlotRange -> {-1, 1}, PlotStyle -> Red], 
  Graphics3D[{Opacity[0.2], Sphere[]}]}]

Answer 2

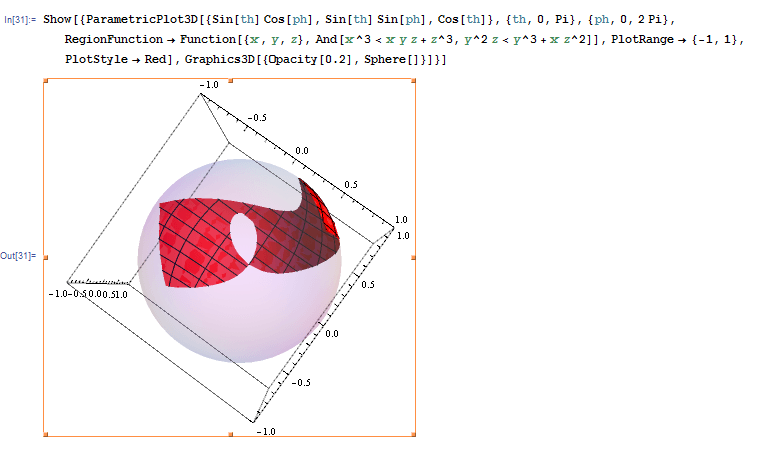
Вот самая простая идея, которую я мог придумать (спасибо Dr. belisarius за часть кода).

• Спроецируйте неравенства на сферу, используя сферические координаты (с θ=q, φ=f).
• Нарисуйте их как плоский участок.
• Затем нарисуйте это как текстуру сферы.

Вот пара однородных неравенств порядка 3

ineq = {x^3 < x y^2, y^2 z > x z^2};

coords = {x -> r Sin[q] Cos[f], y -> r Sin[q] Sin[f], z -> r Cos[q]}/.r -> 1

region = RegionPlot[ineq /. coords, {q, 0, Pi}, {f, 0, 2 Pi}, 
  Frame -> None, ImagePadding -> 0, PlotRangePadding -> 0, ImageMargins -> 0]

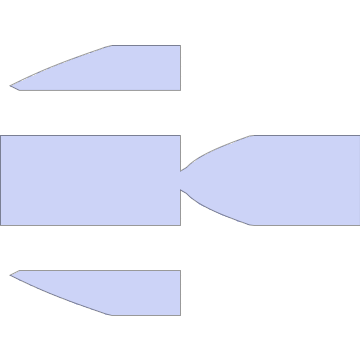
ParametricPlot3D[coords[[All, 2]], {q, 0, Pi}, {f, 0, 2 Pi}, 
 Mesh -> None, TextureCoordinateFunction -> ({#4, 1 - #5} &), 
 PlotStyle -> Texture[Show[region, ImageSize -> 1000]]]

Answer 3

Саймон опередил меня, но вот похожая идея, основанная на графике более низкого уровня. Я имею дело с линейными однородными неравенствами вида Ax>0.

A = RandomReal[{0, 1}, {8, 3}];
eqs = And @@ Thread[
    A.{Sin[phi] Cos[th], Sin[phi] Sin[th], Cos[phi]} >
        Table[0, {Length[A]}]];
twoDPic = RegionPlot[eqs,
    {phi, 0, Pi}, {th, 0, 2 Pi}];
pts2D = twoDPic[[1, 1]];
spherePt[{phi_, th_}] := {Sin[phi] Cos[th], Sin[phi] Sin[th], 
    Cos[phi]};
rpSphere = Graphics3D[GraphicsComplex[spherePt /@ pts2D,
   twoDPic[[1, 2]]]]

Давайте сравним это с RegionPlot3D,

rp3D = RegionPlot3D[And @@ Thread[A.{x, y, z} >
      Table[0, {Length[A]}]],
 {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
   PlotStyle -> Opacity[0.2]];
Show[{rp3D, rpSphere}, PlotRange -> 1.4]

Answer 4

SphericalPlot3D[0.6, {\[Phi], 0, \[Pi]}, {\[Theta], 0, 2 \[Pi]}, 
 RegionFunction -> 
  Function[{x, y, z}, 
   PolyhedronData["Cube", "RegionFunction"][x, y, z]], Mesh -> False, 
 PlotStyle -> {Orange, Opacity[0.9]}]