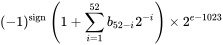Какое наибольшее целочисленное значение в JavaScript может быть достигнуто числом без потери точности?
Это определяется языком? Есть ли определенный максимум? Это отличается в разных браузерах?
25 ответов
+/- 9007199254740991
Обратите внимание, что все положительные и отрицательные целые числа, величина которых не превышает 2 53, представимы в числовом типе (действительно, целое число 0 имеет два представления: +0 и -0).
Это 64-битные значения с плавающей запятой, наибольшее точное целое значение равно 2 53 -1, или 9007199254740991, В ES6 это определяется как Number.MAX_SAFE_INTEGER.
Обратите внимание, что побитовые операторы и операторы сдвига работают с 32-разрядными целыми числами, поэтому в этом случае максимальное безопасное целое число равно 2 31 -1 или 2147483647.
Проверьте это!
var x = 9007199254740992;
var y = -x;
x == x + 1; // true !
y == y - 1; // also true !
// Arithmetic operators work, but bitwise/shifts only operate on int32:
x / 2; // 4503599627370496
x >> 1; // 0
x | 1; // 1
Техническое примечание по теме номера 9007199254740992: Существует точное представление этого значения в IEEE-754, и вы можете присвоить и прочитать это значение из переменной, поэтому для очень тщательно выбранных приложений в области целых чисел, меньших или равных это значение, вы можете рассматривать это как максимальное значение.
В общем случае вы должны рассматривать это значение IEEE-754 как неточное, поскольку неясно, кодирует ли оно логическое значение 9007199254740992 или 9007199254740993.
> = ES6:
Number.MIN_SAFE_INTEGER;
Number.MAX_SAFE_INTEGER;
<= ES5
Из ссылки:
Number.MAX_VALUE;
Number.MIN_VALUE;
console.log('MIN_VALUE', Number.MIN_VALUE);
console.log('MAX_VALUE', Number.MAX_VALUE);
console.log('MIN_SAFE_INTEGER', Number.MIN_SAFE_INTEGER); //ES6
console.log('MAX_SAFE_INTEGER', Number.MAX_SAFE_INTEGER); //ES6Это 253 == 9 007 199 254 740 992. Это потому, что Numbers хранятся в виде плавающей запятой в 52-битной мантиссе.
Минимальное значение -253.
Это делает некоторые забавные вещи, происходящие
Math.pow(2, 53) == Math.pow(2, 53) + 1
>> true
И тоже может быть опасно:)
var MAX_INT = Math.pow(2, 53); // 9 007 199 254 740 992
for (var i = MAX_INT; i < MAX_INT + 2; ++i) {
// infinite loop
}
Дополнительное чтение: http://blog.vjeux.com/2010/javascript/javascript-max_int-number-limits.html
В JavaScript есть число, называемое Infinity,
Примеры:
(Infinity>100)
=> true
// Also worth noting
Infinity - 1 == Infinity
=> true
Math.pow(2,1024) === Infinity
=> true
Это может быть достаточно для некоторых вопросов, касающихся этой темы.
Многие ответы ранее показывают результат true из 9007199254740992 === 9007199254740992 + 1
сказать, что 9 007 199 254 740 991 является максимально безопасным целым числом.
Что если мы продолжим накопление:
input: 9007199254740992 + 1 output: 9007199254740992 // expected: 9007199254740993
input: 9007199254740992 + 2 output: 9007199254740994 // expected: 9007199254740994
input: 9007199254740992 + 3 output: 9007199254740996 // expected: 9007199254740995
input: 9007199254740992 + 4 output: 9007199254740996 // expected: 9007199254740996
Мы могли бы выяснить, что среди чисел больше 9 007 199 254 740 992 представимы только четные числа.
Это запись, объясняющая, как работает 64-битный двоичный формат с двойной точностью. Давайте посмотрим, как 9 007 199 254 740 992 будет проходить (представляться) с использованием этого двоичного формата.
Мы начинаем с 4 503 599 627 370 496 с первой краткой версией формата:
1 . 0000 ---- 0000 * 2^52 => 1 0000 ---- 0000.
|-- 52 bits --| |exponent part| |-- 52 bits --|
В левой части стрелки у нас есть битовое значение 1 и соседняя точка радиуса, затем умножением 2^52 Правильно передвинем основную точку на 52 ступени, и она пойдет до конца. Теперь мы получаем 4503599627370496 в двоичном виде.
Теперь мы начинаем накапливать 1 к этому значению, пока все биты не будут установлены в 1, что равно 9 007 199 254 740 991 в десятичном виде.
1 . 0000 ---- 0000 * 2^52 => 1 0000 ---- 0000.
(+1)
1 . 0000 ---- 0001 * 2^52 => 1 0000 ---- 0001.
(+1)
1 . 0000 ---- 0010 * 2^52 => 1 0000 ---- 0010.
(+1)
.
.
.
1 . 1111 ---- 1111 * 2^52 => 1 1111 ---- 1111.
Теперь, поскольку в 64-битном двоичном формате двойной точности он строго выделяет 52 бита для дроби, больше нет битов, которые можно нести для добавления еще 1, поэтому мы могли бы установить все биты обратно в 0 и манипулировать ими. экспонентная часть:
|--> This bit is implicit and persistent.
|
1 . 1111 ---- 1111 * 2^52 => 1 1111 ---- 1111.
|-- 52 bits --| |-- 52 bits --|
(+1)
(radix point have no way to go)
1 . 0000 ---- 0000 * 2^52 * 2 => 1 0000 ---- 0000. * 2
|-- 52 bits --| |-- 52 bits --|
=> 1 . 0000 ---- 0000 * 2^53
|-- 52 bits --|
Теперь мы получаем 9 007 199 254 740 992, и с числом, большим его, формат может быть в 2 раза больше дроби:
(consume 2^52 to move radix point to the end)
1 . 0000 ---- 0001 * 2^53 => 1 0000 ---- 0001. * 2
|-- 52 bits --| |-- 52 bits --|
Таким образом, когда число становится больше, чем 9 007 199 254 740 992 * 2 = 18 014 398 509 481 984, может быть проведено только 4 раза дроби:
input: 18014398509481984 + 1 output: 18014398509481984 // expected: 18014398509481985
input: 18014398509481984 + 2 output: 18014398509481984 // expected: 18014398509481986
input: 18014398509481984 + 3 output: 18014398509481984 // expected: 18014398509481987
input: 18014398509481984 + 4 output: 18014398509481988 // expected: 18014398509481988
Как насчет числа между [ 2 251 799 813 685 248, 4 503 599 627 370 496)?
1 . 0000 ---- 0001 * 2^51 => 1 0000 ---- 000.1
|-- 52 bits --| |-- 52 bits --|
Битовое значение 1 после радикальной точки равно 2^-1. (=1/2, =0,5) Таким образом, когда число меньше 4 503 599 627 370 496 (2^52), есть один доступный бит для представления 1/2 раз целого числа:
input: 4503599627370495.5 output: 4503599627370495.5
input: 4503599627370495.75 output: 4503599627370495.5
Менее 2 251 799 813 685 248 (2 ^ 51)
input: 2251799813685246.75 output: 2251799813685246.8 // expected: 2251799813685246.75
input: 2251799813685246.25 output: 2251799813685246.2 // expected: 2251799813685246.25
input: 2251799813685246.5 output: 2251799813685246.5
// If the digits exceed 17, JavaScript round it to print it.
//, but the value is held correctly:
input: 2251799813685246.25.toString(2)
output: "111111111111111111111111111111111111111111111111110.01"
input: 2251799813685246.75.toString(2)
output: "111111111111111111111111111111111111111111111111110.11"
input: 2251799813685246.78.toString(2)
output: "111111111111111111111111111111111111111111111111110.11"
И каков доступный диапазон экспонентной части? формат выделяет для него 11 битов. Полный формат из Wiki: (для более подробной информации, пожалуйста, перейдите туда)
Таким образом, чтобы получить 2^52 в экспоненциальной части, нам точно нужно установить e = 1075.
Ответ Джимми правильно представляет непрерывный целочисленный спектр JavaScript как от -9007199254740992 до 9007199254740992 включительно (извините, 9007199254740993, вы можете подумать, что вы 9007199254740993, но вы ошибаетесь! Демонстрация ниже или в jsfiddle).
document.write(9007199254740993);Тем не менее, нет ответа, который находит / доказывает это программно (кроме того, на который ссылается CoolAJ86 в своем ответе, который закончится через 28,56 лет;), так что вот немного более эффективный способ сделать это (точнее, это более эффективно примерно на 28,559999999968312 лет:) вместе с испытательной скрипкой:
/**
* Checks if adding/subtracting one to/from a number yields the correct result.
*
* @param number The number to test
* @return true if you can add/subtract 1, false otherwise.
*/
var canAddSubtractOneFromNumber = function(number) {
var numMinusOne = number - 1;
var numPlusOne = number + 1;
return ((number - numMinusOne) === 1) && ((number - numPlusOne) === -1);
}
//Find the highest number
var highestNumber = 3; //Start with an integer 1 or higher
//Get a number higher than the valid integer range
while (canAddSubtractOneFromNumber(highestNumber)) {
highestNumber *= 2;
}
//Find the lowest number you can't add/subtract 1 from
var numToSubtract = highestNumber / 4;
while (numToSubtract >= 1) {
while (!canAddSubtractOneFromNumber(highestNumber - numToSubtract)) {
highestNumber = highestNumber - numToSubtract;
}
numToSubtract /= 2;
}
//And there was much rejoicing. Yay.
console.log('HighestNumber = ' + highestNumber);Быть в безопасности
var MAX_INT = 4294967295;
аргументация
Я думал, что я буду умным и найду значение, при котором x + 1 === x с более прагматичным подходом.
Моя машина может считать только 10 миллионов в секунду или около того... поэтому я отправлю ответ с окончательным ответом через 28,56 лет.
Если вы не можете ждать так долго, я готов поспорить, что
- Большинство ваших петель не работают в течение 28,56 лет
9007199254740992 === Math.pow(2, 53) + 1достаточно доказательств- Вы должны придерживаться
4294967295которыйMath.pow(2,32) - 1чтобы избежать ожидаемых проблем со сдвигом битов
обнаружение x + 1 === x:
(function () {
"use strict";
var x = 0
, start = new Date().valueOf()
;
while (x + 1 != x) {
if (!(x % 10000000)) {
console.log(x);
}
x += 1
}
console.log(x, new Date().valueOf() - start);
}());
Краткий ответ "это зависит".
Если вы где-либо используете побитовые операторы (или если вы ссылаетесь на длину массива), диапазоны:
Unsigned: 0…(-1>>>0)
Подпись: (-(-1>>>1)-1)…(-1>>>1)
(Бывает, что побитовые операторы и максимальная длина массива ограничены 32-битными целыми числами.)
Если вы не используете побитовые операторы или не работаете с длинами массива:
Подпись: (-Math.pow(2,53))…(+Math.pow(2,53))
Эти ограничения накладываются внутренним представлением типа "Число", которое в целом соответствует представлению с плавающей точкой двойной точности IEEE 754. (Обратите внимание, что в отличие от типичных целых чисел со знаком, величина отрицательного предела такая же, как величина положительного предела, из-за характеристик внутреннего представления, которое фактически включает отрицательный 0!)
ECMAScript 6:
Number.MAX_SAFE_INTEGER = Math.pow(2, 53)-1;
Number.MIN_SAFE_INTEGER = -Number.MAX_SAFE_INTEGER;
Другие, возможно, уже дали общий ответ, но я подумал, что было бы неплохо дать быстрый способ его определения:
for (var x = 2; x + 1 !== x; x *= 2);
console.log(x);
Что дает мне 9007199254740992 менее чем за миллисекунду в Chrome 30.
Он проверит степень 2, чтобы определить, какой из них, когда "добавлен" 1, равен себе.
Все, что вы хотите использовать для побитовых операций, должно быть в диапазоне от 0x80000000 (-2147483648 или -2^31) до 0x7fffffff (2147483647 или 2^31 - 1).
Консоль сообщит вам, что 0x80000000 равно +2147483648, но 0x80000000 & 0x80000000 равно -2147483648.
На момент написания JavaScript получает новый тип данных: BigInt, Это предложение TC39 на этапе 3. BigInt был отправлен в Chrome и находится в стадии разработки в Node, Firefox и Safari... Он вводит числовые литералы с суффиксом "n" и допускает произвольную точность:
var a = 123456789012345678901012345678901n;
Конечно, точность все равно будет потеряна, когда такое число (возможно, непреднамеренно) приведено к типу данных числа.
Я провел простой тест с формулой X-(X+1)=-1, и наибольшее значение X I, которое можно получить для работы в Safari, Opera и Firefox (протестировано в OS X) - 9e15. Вот код, который я использовал для тестирования:
javascript: alert(9e15-(9e15+1));
Давайте перейдем к источникам
Описание
MAX_SAFE_INTEGERконстанта имеет значение9007199254740991(9 007 199 254 740 991 или ~9 квадриллионов). Причина этого числа заключается в том, что JavaScript использует числа в формате с плавающей запятой двойной точности, как указано в IEEE 754, и может безопасно представлять числа только между-(253 - 1)а также253 - 1,Безопасный в этом контексте относится к способности точно представлять целые числа и правильно их сравнивать. Например,
Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2будет оценивать как истинное, что математически неверно. См. Number.isSafeInteger() для получения дополнительной информации.Так как
MAX_SAFE_INTEGERявляется статическим свойством Number, вы всегда используете его какNumber.MAX_SAFE_INTEGER, а не как свойство созданного вами объекта Number.
Совместимость браузера
Я пишу это так:
var max_int = 0x20000000000000;
var min_int = -0x20000000000000;
(max_int + 1) === 0x20000000000000; //true
(max_int - 1) < 0x20000000000000; //true
То же самое для int32
var max_int32 = 0x80000000;
var min_int32 = -0x80000000;
В JavaScript представление чисел 2^53 - 1,
Тем не менее, Bitwise operation рассчитаны на 32 bits ( 4 bytes ) Это означает, что если вы превысите 32-битные смены, вы начнете терять биты.
По сути, JavaScript не поддерживает долго.
поэтому для нормальных значений, которые он может представлять менее 32 бит, он будет использовать контейнер типа int. для целочисленных значений больше 32 бит используется двойное. В двойном представлении целочисленная часть составляет 53 бита, а остальное - мантисса (для хранения информации с плавающей запятой).
так что вы можете использовать 2^53 - 1 какое значение 9007199254740991
Вы можете получить доступ к значению для использования в вашем коде Number.MAX_SAFE_INTEGER
Когда число больше 2 до степени 53, т.е.
Math.pow(2, 53)
JavaScript знает это как большое целое число. Затем javascript сохраняет их как "big int", так что по сравнению с 'bigint'==='bigint' становится правдой.
Более безопасный способ хранить их значения в самом объекте Math.
const bigInt1 = Math.pow(2, 55)
const bigInt2 = Math.pow(2, 66)
console.log(bigInt1 === bigInt2) // false
Как найти максимальное целочисленное значение
console.log(2 ** 53 - 1);
console.log(Number.MAX_SAFE_INTEGER);
Выход: 9007199254740993
Number.MAX_VALUE представляет максимальное числовое значение, представляемое в JavaScript.
Так как никто, кажется, не сказал так, в двигателе v8 есть разница в поведении для 31 bits номер и номер выше этого.
Если у вас есть 32 bits Вы можете использовать первый бит, чтобы сообщить движку javascript, к какому типу относятся эти данные, а оставшиеся биты содержат фактические данные. Вот что делает V8 как небольшая оптимизация для 31 bisnumbers (или раньше, мои источники довольно устарели). У вас последний 31 bits это числовое значение, а затем первый бит, сообщающий движку, является ли это число или ссылка на объект.
Однако, если вы используете номер выше 31 bits тогда данные не будут вписываться, число будет упаковано в двойные 64-битные числа, и оптимизации не будет.
Нижняя строка в видео ниже:
предпочитайте числовые значения, которые могут быть представлены как целые числа со знаком 31 бит.
Во встроенном JavaScript Google Chrome вы можете перейти примерно к 2^1024, прежде чем число будет называться бесконечностью.
Scato wrotes:
все, что вы хотите использовать для побитовых операций, должно быть в диапазоне от 0x80000000 (-2147483648 или -2^31) до 0x7fffffff (2147483647 или 2^31 - 1).
консоль скажет вам, что 0x80000000 равно +2147483648, но 0x80000000 & 0x80000000 равно -2147483648
Шестнадцатеричные десятичные числа являются положительными значениями без знака, поэтому 0x80000000 = 2147483648 - это математически правильно. Если вы хотите сделать его значением со знаком, вам нужно сдвинуть вправо: 0x80000000 >> 0 = -2147483648. Вместо этого вы также можете написать 1 << 31.
Node.js и Google Chrome, похоже, используют 1024-битные значения с плавающей запятой, поэтому:
Number.MAX_VALUE = 1.7976931348623157e+308
У Firefox 3, похоже, нет проблем с огромными числами.
1e + 200 * 1e + 100 - штраф до 1e+300.
У Safari, похоже, нет проблем с этим. (Для справки, это на Mac, если кто-то еще решит проверить это.)
Если я не потерял свой мозг в это время дня, это намного больше, чем 64-разрядное целое число.