Накладные расходы на коды с исправлением ошибок при увеличении частоты ошибок

Question

Накладные расходы на коды с исправлением ошибок при увеличении частоты ошибок

Я ищу помощь в понимании того, что накладные расходы (количество дополнительных символов, которые должны быть переданы) связаны с кодами, исправляющими ошибки (например, с помощью кода Рида-Соломона), так как частота ошибок, для которых она предназначена, увеличивается. Например, если процесс должен иметь возможность исправить 1 неправильный символ на 500, что это за издержки по сравнению с 1 из 100.

Я понимаю, что на практике эти сложные схемы часто используются (на компакт-дисках используются перекрывающиеся наборы кодирования и т. Д.), Но сначала я пытаюсь понять простейший случай. Является ли соотношение между служебной нагрузкой и частотой ошибок приблизительно линейным? Квадратное? Экспоненциальный? Я понимаю, что обозначение Big O не является подходящим инструментом, поэтому, пожалуйста, прости меня, если математическое сообщество обычно не формулирует проблему.

Я был бы взволнован за ответ, который вычислил накладные расходы, связанные со следующей частотой ошибок для кодирования Рида-Соломона:

Ошибка 1 символа на 10000 Ошибка 1 символа на 2000 Ошибка 1 символа на 1000 Ошибка 1 символа на 500 Ошибка 1 символа на 50

2

math error-correction reed-solomon

Источник

user343633 26 июн '14 в 01:59

1 ответ

Решение

Другие вопросы по тегам math error-correction reed-solomon

user1468366 26 июн '14 в 09:36 2014-06-26 09:36 · Accepted Answer · 2014-06-26 09:36

Ищите Хэмминга связанного. Там вы прочтете, что код с расстоянием Хэмминга d, т. Е. Который может обнаружить d − 1 однозначные ошибки и исправить t = ⌊ (d − 1) / 2⌋ однозначные ошибки, имеет размер не более

$Гидроразрыва {д ^ п} {\ displaystyle \ sum_ {к = 0} ^ т \ БИНОМ {п} {K} (Q-1) ^ к$

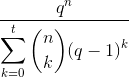
разные кодовые слова. Теперь для простейшего случая предположим двоичные коды. Итак, примите q = 2 в качестве размера алфавита и n = 2 ^b в качестве количества кодовых слов в b битах. Тогда логарифм по основанию два вышеупомянутой границы даст вам максимальное количество битов, которое вы можете фактически передать, а скорость кодирования будет отношением между этими двумя битами.

Когда вы выражаете скорость кода в терминах толерантности к ошибкам, вы можете захотеть изучить ограничение для больших кодовых слов. Чтобы это имело смысл, вы должны превратить абсолютное количество ошибок в частоту ошибок, чтобы количество ошибок было пропорционально длине кода. Тогда должно быть возможно получить полезные ограничения.