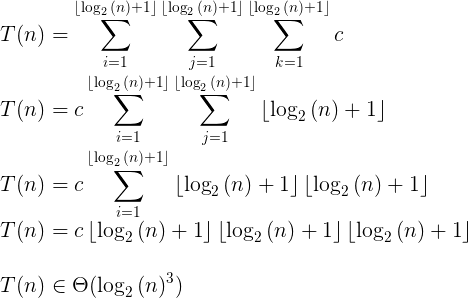Java Big O нотация 3-х вложенных циклов журнала (n)

Question

Что обозначение Big O будет для следующих вложенных циклов?

     for (int i = n; i > 0; i = i / 2){
        for (int j = n; j > 0; j = j / 2){
           for (int k = n; k > 0; k = k / 2){
              count++;
           }
        }
     }

Мои мысли: каждая петля O(log2(n)) так же просто, как умножить

O(log2(n)) * O(log2(n)) * O(log2(n))  =  O(log2(n)^3)

Answer 1

Да, это правильно.

Один из способов выяснить сложность вложенных циклов big-O, границы которых не зависят друг от друга, - это работать изнутри. Внутренний цикл выполняет O (log n). Второй цикл выполняется O (log n) раз и O (log n) работает каждый раз, поэтому он выполняет O (log² n). Наконец, самый внешний цикл выполняется O (log n) раз и O (log² n) работает на каждой итерации, поэтому общая работа - O (log³ n).

Надеюсь это поможет!

Answer 2

Да ты прав.

Простой способ рассчитать -

for(int i=0; i<n;i++){ // n times 
    for(int j=0; j<n;j++){ // n times
    }
}

Это пример простого вложенного цикла. Здесь Big-O каждого цикла O(n) и он вложен так, как правило, O(n * n), который является O(n^2), фактическим Big-O. А в твоем случае -

for (int i = n; i > 0; i = i / 2){ // log(n)
     for (int j = n; j > 0; j = j / 2){ // log(n)
         for (int k = n; k > 0; k = k / 2){ // log(n)
           count++;
         }
     }
}

Который находится во вложенном цикле, где каждый цикл Big-O O(log(n)) так что все вместе сложность будет O(log(n)^3)

Answer 3

Действительно, ваше предположение верно. Вы можете показать это методично следующим образом: