Почему истекшее время увеличивается, а количество ядер увеличивается?
Я делаю многоядерные вычисления в R. Я
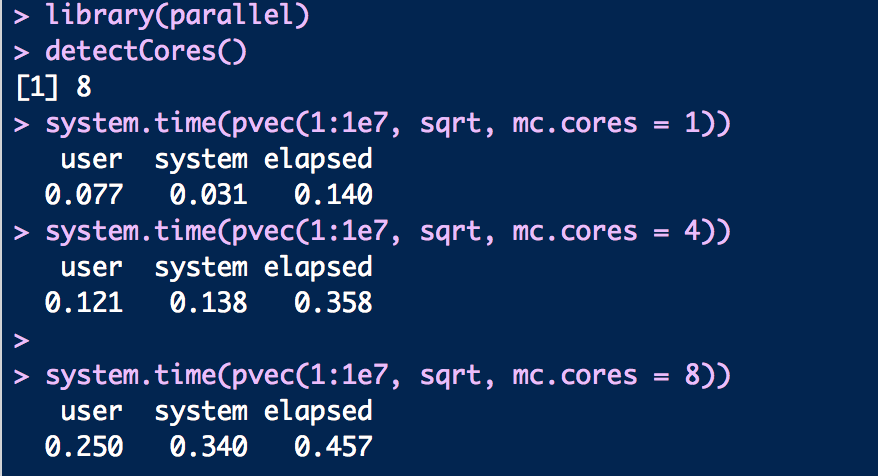
Вот код и выходные данные для каждого вычисления. Почему истекшее время увеличивается с увеличением количества ядер? Это действительно нелогично. Я думаю, что разумно, что истекшее время уменьшается с увеличением количества ядер. Есть ли способ это исправить?
Вот код:
library(parallel)
detectCores()
system.time(pvec(1:1e7, sqrt, mc.cores = 1))
system.time(pvec(1:1e7, sqrt, mc.cores = 4))
system.time(pvec(1:1e7, sqrt, mc.cores = 8))
Спасибо.
1 ответ
Предположим, что ваши данные разделены на N частей. Каждая часть ваших данных рассчитывается в T секунд. В одноядерной архитектуре вы ожидаете, что все операции будут выполнены за N x T секунд. Вы также надеетесь, что все работы должны быть выполнены в T раз на машине с N ядрами. Однако в параллельных вычислениях существует задержка связи, которая потребляется каждым отдельным ядром (инициализация, передача данных от основного к дочернему, вычисления, передача результата и финализация). Теперь пусть коммуникационная задержка составляет C секунд и для простоты она постоянна для всех ядер. Таким образом, в машине с N ядрами расчеты должны выполняться в
Т + Н х С
секунд, в которых часть T предназначена для вычислений, а часть N X C - для общего обмена данными. Если мы сравним это с одноядерным компьютером, неравенство
(Н х Т) > (Т + Н х С)
должно быть удовлетворено, чтобы получить время вычисления, по крайней мере, для наших предположений. Если мы упростим неравенство, мы можем получить
C <(N x T - T) / N
Итак, если постоянное время связи не меньше, чем отношение (N x T - T) / N, у нас нет никакой выгоды, чтобы сделать это вычисление параллельным.
В вашем примере время, необходимое для создания, расчета и связи, больше, чем одноядерное вычисление для функции sqrt.