Более быстрый способ инициализации массивов с помощью умножения пустой матрицы? (Matlab)
Я наткнулся на странный (на мой взгляд) способ, которым Matlab имеет дело с пустыми матрицами. Например, если умножить две пустые матрицы, результат будет:
zeros(3,0)*zeros(0,3)
ans =
0 0 0
0 0 0
0 0 0
Теперь, это уже застало меня врасплох, однако быстрый поиск привел меня к ссылке выше, и я получил объяснение несколько искаженной логики того, почему это происходит.
Однако ничто не подготовило меня к следующему наблюдению. Я спросил себя, насколько эффективен этот тип умножения против простого использования zeros(n) Функция, скажем, с целью инициализации? Я использовал timeit чтобы ответить на это:
f=@() zeros(1000)
timeit(f)
ans =
0.0033
против:
g=@() zeros(1000,0)*zeros(0,1000)
timeit(g)
ans =
9.2048e-06
Оба имеют одинаковый результат 1000x1000 матрицы нулей класса double, но умножение пустой матрицы 1 происходит в ~350 раз быстрее! (аналогичный результат происходит с использованием tic а также toc и петля)
Как это может быть? являются timeit или же tic,toc блеф или я нашел более быстрый способ инициализации матриц?
(это было сделано с помощью matlab 2012a, на машине win7-64, intel-i5 650 3.2Ghz...)
РЕДАКТИРОВАТЬ:
После прочтения вашего отзыва я более внимательно изучил эту особенность и протестировал на 2 разных компьютерах (один и тот же код версии 2012a) код, который проверяет время выполнения в зависимости от размера матрицы n. Вот что я получаю:
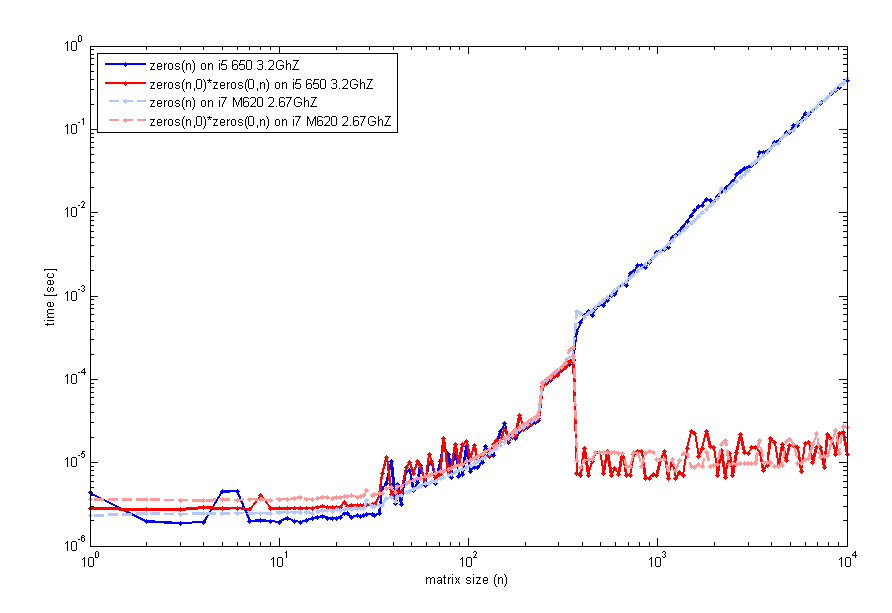
Код для создания этого используется timeit как и раньше, но петля с tic а также toc будет выглядеть так же. Итак, для небольших размеров, zeros(n) сопоставим. Тем не менее, вокруг n=400 для умножения пустой матрицы наблюдается скачок производительности. Код, который я использовал для создания этого графика, был:
n=unique(round(logspace(0,4,200)));
for k=1:length(n)
f=@() zeros(n(k));
t1(k)=timeit(f);
g=@() zeros(n(k),0)*zeros(0,n(k));
t2(k)=timeit(g);
end
loglog(n,t1,'b',n,t2,'r');
legend('zeros(n)','zeros(n,0)*zeros(0,n)',2);
xlabel('matrix size (n)'); ylabel('time [sec]');
Кто-нибудь из вас тоже испытывает это?
РЕДАКТИРОВАТЬ № 2:
Кстати, для получения этого эффекта умножение пустой матрицы не требуется. Можно просто сделать:
z(n,n)=0;
где n> некоторый пороговый размер матрицы, видимый на предыдущем графике, и получить точный профиль эффективности, как при умножении пустой матрицы (снова используя timeit).
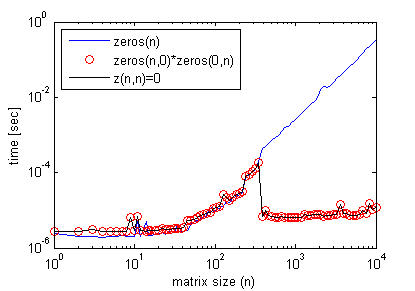
Вот пример, где это улучшает эффективность кода:
n = 1e4;
clear z1
tic
z1 = zeros( n );
for cc = 1 : n
z1(:,cc)=cc;
end
toc % Elapsed time is 0.445780 seconds.
%%
clear z0
tic
z0 = zeros(n,0)*zeros(0,n);
for cc = 1 : n
z0(:,cc)=cc;
end
toc % Elapsed time is 0.297953 seconds.
Однако, используя z(n,n)=0; вместо этого дает результаты, аналогичные zeros(n) дело.
5 ответов
Это странно, я вижу, что быстрее, а медленнее, чем то, что вы видите. Но оба они идентичны для меня. Возможно, другая версия MATLAB?
>> g = @() zeros(1000, 0) * zeros(0, 1000);
>> f = @() zeros(1000)
f =
@()zeros(1000)
>> timeit(f)
ans =
8.5019e-04
>> timeit(f)
ans =
8.4627e-04
>> timeit(g)
ans =
8.4627e-04
РЕДАКТИРОВАТЬ вы можете добавить + 1 в конце f и g, и посмотреть, сколько раз вы получаете.
РЕДАКТИРОВАТЬ 6 января 2013 7:42 EST
Я пользуюсь машиной удаленно, поэтому извините за некачественные графики (пришлось генерировать их вслепую).
Конфигурация машины:
i7 920. 2,663 ГГц. Linux. 12 ГБ ОЗУ. 8 МБ кеша.
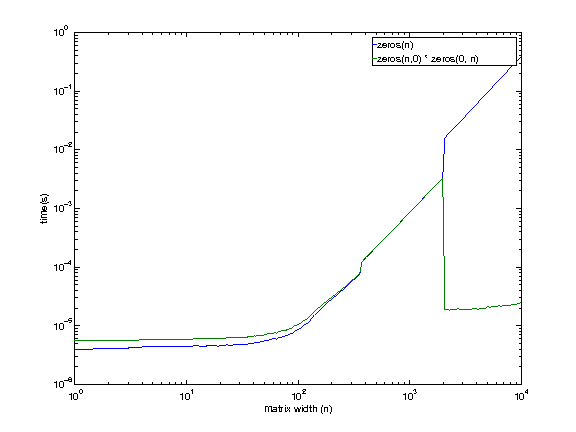
Похоже, что даже машина, к которой у меня есть доступ, демонстрирует такое поведение, кроме как в большем размере (где-то между 1979 и 2073 годами). Сейчас нет причин думать, чтобы умножение пустой матрицы было быстрее при больших размерах.
Я буду исследовать немного больше, прежде чем вернуться.
РЕДАКТИРОВАТЬ 11 января 2013 г.
После публикации @EitanT я хотел еще немного покопаться. Я написал немного кода на C, чтобы увидеть, как matlab может создавать матрицу нулей. Вот код C++, который я использовал.
int main(int argc, char **argv)
{
for (int i = 1975; i <= 2100; i+=25) {
timer::start();
double *foo = (double *)malloc(i * i * sizeof(double));
for (int k = 0; k < i * i; k++) foo[k] = 0;
double mftime = timer::stop();
free(foo);
timer::start();
double *bar = (double *)malloc(i * i * sizeof(double));
memset(bar, 0, i * i * sizeof(double));
double mmtime = timer::stop();
free(bar);
timer::start();
double *baz = (double *)calloc(i * i, sizeof(double));
double catime = timer::stop();
free(baz);
printf("%d, %lf, %lf, %lf\n", i, mftime, mmtime, catime);
}
}
Вот результаты.
$ ./test
1975, 0.013812, 0.013578, 0.003321
2000, 0.014144, 0.013879, 0.003408
2025, 0.014396, 0.014219, 0.003490
2050, 0.014732, 0.013784, 0.000043
2075, 0.015022, 0.014122, 0.000045
2100, 0.014606, 0.014480, 0.000045
Как вы видете calloc (4-й столбец), кажется, самый быстрый метод. Между 2025 и 2050 годами он также значительно ускоряется (я бы предположил, что в 2048?).
Теперь я вернулся в Matlab, чтобы проверить то же самое. Вот результаты.
>> test
1975, 0.003296, 0.003297
2000, 0.003377, 0.003385
2025, 0.003465, 0.003464
2050, 0.015987, 0.000019
2075, 0.016373, 0.000019
2100, 0.016762, 0.000020
Похоже, что f () и g () используют calloc в меньших размерах (<2048?). Но при больших размерах f () (нули (m, n)) начинает использовать malloc + memsetв то время как g () (нули (m, 0) * нули (0, n)) продолжает использовать calloc,
Таким образом, расхождение объясняется следующим
- нули (..) начинают использовать другую (более медленную?) схему при больших размерах.
callocтакже ведет себя несколько неожиданно, что приводит к улучшению производительности.
Это поведение в Linux. Может ли кто-нибудь провести такой же эксперимент на другой машине (и, возможно, на другой ОС) и посмотреть, если эксперимент удастся?
Результаты могут быть немного вводящими в заблуждение. Когда вы умножаете две пустые матрицы, результирующая матрица не сразу "выделяется" и "инициализируется", а скорее откладывается до тех пор, пока вы не используете ее в первый раз (что-то вроде ленивой оценки).
То же самое относится и к индексированию вне границ для увеличения переменной, которая в случае числовых массивов заполняет все пропущенные записи нулями (позже я расскажу о нечисловом регистре). Конечно, увеличение матрицы таким способом не перезаписывает существующие элементы.
Таким образом, хотя это может показаться быстрее, вы просто откладываете время выделения, пока не начнете использовать матрицу. В конце у вас будут такие же сроки, как если бы вы делали распределение с самого начала.
Пример, демонстрирующий это поведение, по сравнению с несколькими другими альтернативами:
N = 1000;
clear z
tic, z = zeros(N,N); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = zeros(N,0)*zeros(0,N); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z(N,N) = 0; toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = full(spalloc(N,N,0)); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z(1:N,1:N) = 0; toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
val = 0;
tic, z = val(ones(N)); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = repmat(0, [N N]); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
Результат показывает, что если вы суммируете прошедшее время для обеих инструкций в каждом случае, вы получите схожие общие значения времени:
// zeros(N,N)
Elapsed time is 0.004525 seconds.
Elapsed time is 0.000792 seconds.
// zeros(N,0)*zeros(0,N)
Elapsed time is 0.000052 seconds.
Elapsed time is 0.004365 seconds.
// z(N,N) = 0
Elapsed time is 0.000053 seconds.
Elapsed time is 0.004119 seconds.
Другие сроки были:
// full(spalloc(N,N,0))
Elapsed time is 0.001463 seconds.
Elapsed time is 0.003751 seconds.
// z(1:N,1:N) = 0
Elapsed time is 0.006820 seconds.
Elapsed time is 0.000647 seconds.
// val(ones(N))
Elapsed time is 0.034880 seconds.
Elapsed time is 0.000911 seconds.
// repmat(0, [N N])
Elapsed time is 0.001320 seconds.
Elapsed time is 0.003749 seconds.
Эти измерения слишком малы в миллисекундах и могут быть не очень точными, поэтому вы можете выполнить эти команды в цикле несколько тысяч раз и получить среднее значение. Также иногда запуск сохраненных M-функций выполняется быстрее, чем выполнение сценариев или командной строки, поскольку некоторые оптимизации происходят только таким образом...
В любом случае распределение обычно выполняется один раз, так что кого это волнует, если это займет дополнительные 30 мс:)
Подобное поведение можно наблюдать с массивами клеток или массивами структур. Рассмотрим следующий пример:
N = 1000;
tic, a = cell(N,N); toc
tic, b = repmat({[]}, [N,N]); toc
tic, c{N,N} = []; toc
который дает:
Elapsed time is 0.001245 seconds.
Elapsed time is 0.040698 seconds.
Elapsed time is 0.004846 seconds.
Обратите внимание, что даже если они все равны, они занимают разное количество памяти:
>> assert(isequal(a,b,c))
>> whos a b c
Name Size Bytes Class Attributes
a 1000x1000 8000000 cell
b 1000x1000 112000000 cell
c 1000x1000 8000104 cell
На самом деле ситуация здесь немного сложнее, поскольку MATLAB, вероятно, использует одну и ту же пустую матрицу для всех ячеек, а не создает несколько копий.
Массив ячеек a на самом деле это массив неинициализированных ячеек (массив указателей NULL), тогда как b это массив ячеек, где каждая ячейка является пустым массивом [] (внутренне и из-за обмена данными, только первая ячейка b{1} указывает на [] в то время как все остальные имеют ссылку на первую ячейку). Конечный массив c похож на a (неинициализированные ячейки), но последняя содержит пустую числовую матрицу [],
Я посмотрел список экспортируемых функций C из libmx.dll (используя инструмент Dependency Walker), и я нашел несколько интересных вещей.
Есть недокументированные функции для создания неинициализированных массивов:
mxCreateUninitDoubleMatrix,mxCreateUninitNumericArray, а такжеmxCreateUninitNumericMatrix, На самом деле есть представление на файловой бирже использует эти функции, чтобы обеспечить более быструю альтернативуzerosфункция.существует недокументированная функция под названием
mxFastZeros, Погуглив онлайн, я вижу, что вы ответили на этот вопрос в ответах на MATLAB, и там есть несколько отличных ответов. Джеймс Турса (тот же автор UNINIT, что и раньше) привел пример использования этой недокументированной функции.libmx.dllсвязано сtbbmalloc.dllобщая библиотека Это масштабируемый распределитель памяти Intel TBB. Эта библиотека предоставляет эквивалентные функции выделения памяти (malloc,calloc,free) оптимизирован для параллельных приложений. Помните, что многие функции MATLAB автоматически являются многопоточными, поэтому я не удивлюсь, еслиzeros(..)является многопоточным и использует распределитель памяти Intel, когда размер матрицы достаточно велик (вот недавний комментарий Лорен Шуре, который подтверждает этот факт).
Что касается последнего пункта о распределителе памяти, вы можете написать аналогичный эталонный тест на C/C++, аналогичный тому, что делал @PavanYalamanchili, и сравнить различные доступные распределители. Как то так Помните, что MEX-файлы имеют немного больше накладных расходов на управление памятью, поскольку MATLAB автоматически освобождает любую память, которая была выделена в MEX-файлах, используя mxCalloc, mxMalloc, или же mxRealloc функции. Для чего это стоило, раньше было возможно изменить менеджер внутренней памяти в старых версиях.
РЕДАКТИРОВАТЬ:
Вот более тщательный тест для сравнения обсуждаемых альтернатив. Это конкретно показывает, что, как только вы подчеркиваете использование всей выделенной матрицы, все три метода находятся в равных условиях, и разница незначительна.
function compare_zeros_init()
iter = 100;
for N = 512.*(1:8)
% ZEROS(N,N)
t = zeros(iter,3);
for i=1:iter
clear z
tic, z = zeros(N,N); t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, ZEROS = %.9f\n', N, mean(sum(t,2)))
% z(N,N)=0
t = zeros(iter,3);
for i=1:iter
clear z
tic, z(N,N) = 0; t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, GROW = %.9f\n', N, mean(sum(t,2)))
% ZEROS(N,0)*ZEROS(0,N)
t = zeros(iter,3);
for i=1:iter
clear z
tic, z = zeros(N,0)*zeros(0,N); t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, MULT = %.9f\n\n', N, mean(sum(t,2)))
end
end
Ниже приведены временные значения, усредненные за 100 итераций с точки зрения увеличения размера матрицы. Я выполнил тесты в R2013a.
>> compare_zeros_init
N = 512, ZEROS = 0.001560168
N = 512, GROW = 0.001479991
N = 512, MULT = 0.001457031
N = 1024, ZEROS = 0.005744873
N = 1024, GROW = 0.005352638
N = 1024, MULT = 0.005359236
N = 1536, ZEROS = 0.011950846
N = 1536, GROW = 0.009051589
N = 1536, MULT = 0.008418878
N = 2048, ZEROS = 0.012154002
N = 2048, GROW = 0.010996315
N = 2048, MULT = 0.011002169
N = 2560, ZEROS = 0.017940950
N = 2560, GROW = 0.017641046
N = 2560, MULT = 0.017640323
N = 3072, ZEROS = 0.025657999
N = 3072, GROW = 0.025836506
N = 3072, MULT = 0.051533432
N = 3584, ZEROS = 0.074739924
N = 3584, GROW = 0.070486857
N = 3584, MULT = 0.072822335
N = 4096, ZEROS = 0.098791732
N = 4096, GROW = 0.095849788
N = 4096, MULT = 0.102148452
Проведя некоторое исследование, я нашел эту статью в "Недокументированном Matlab", в котором Yair Altman уже пришел к выводу, что способ MathWork по предварительному выделению матриц с использованием zeros(M, N) это действительно не самый эффективный способ.
Он приурочен x = zeros(M,N) против clear x, x(M,N) = 0 и обнаружил, что последний в ~500 раз быстрее. Согласно его объяснению, второй метод просто создает матрицу M-by-N, элементы которой автоматически инициализируются равными 0. Однако первый метод создает x (с x имеет автоматический нулевой элемент), а затем присваивает ноль каждому элементу в x снова, и это избыточная операция, которая занимает больше времени.
В случае умножения пустой матрицы, такого как то, что вы показали в своем вопросе, MATLAB ожидает, что продукт будет матрицей M×N, и поэтому он выделяет матрицу M×N. Следовательно, выходная матрица автоматически инициализируется нулями. Поскольку исходные матрицы пусты, дальнейшие вычисления не выполняются, и, следовательно, элементы в выходной матрице остаются неизменными и равными нулю.
Интересный вопрос, по-видимому, есть несколько способов "обыграть" встроенный zeros функция. Мое единственное предположение относительно того, почему это происходит, состоит в том, что это может быть более эффективным с точки зрения памяти (в конце концов, zeros(LargeNumer) скорее приведет к тому, что Matlab достигнет предела памяти, чем создаст опустошающее узкое место в скорости в большинстве кода), или станет более надежным.
Вот еще один метод быстрого распределения, использующий разреженную матрицу, в качестве эталона я добавил функцию регулярных нулей:
tic; x=zeros(1000,1000); toc
Elapsed time is 0.002863 seconds.
tic; clear x; x(1000,1000)=0; toc
Elapsed time is 0.000282 seconds.
tic; x=full(spalloc(1000,1000,0)); toc
Elapsed time is 0.000273 seconds.
tic; x=spalloc(1000,1000,1000000); toc %Is this the same for practical purposes?
Elapsed time is 0.000281 seconds.
Этот ответ сфальсифицирован. Хранится только для записи. Кажется, Matlab решает использовать разреженные матрицы, когда он получил команду, как z(n,n)=0; когда n достаточно велико. Внутренняя реализация может быть в форме условия, такого как: (если newsize>THRESHOLD+oldsize, тогда используйте sparse...) где THRESHOLD - ваш "пороговый размер".
Однако это несмотря на утверждение Mathworks: "Matlab никогда не создает разреженные матрицы автоматически" ( ссылка)
У меня нет Matlab, чтобы проверить это. Тем не менее, использование разреженных матриц (внутренне) является более коротким объяснением (бритва Оккама), поэтому лучше до фальсификации.