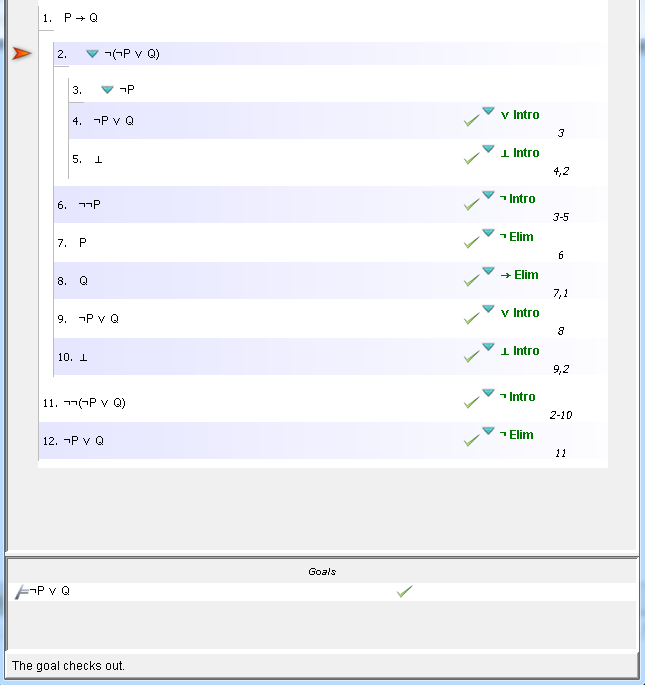
Формальное доказательство для P → Q ≡ ¬P ∨ Q в Fitch

Question

Я пытаюсь построить формальное доказательство для "P → Q ≡ ¬P ∨ Q" в Fitch. Я знаю, что это правда, но как мне доказать это?

Answer 1

Мне наконец удалось решить это:

довольно прямо вперед

Answer 2

Учитывая p ⇒ q, используйте систему Fitch, чтобы доказать ¬p ∨ q.

1.  p => q            Premise
2.    ~(~p | q)       Assumption
3.      ~p            Assumption
4.      ~p | q        Or Introduction: 3
5.    ~p => ~p | q    Implication Introduction: 3, 4
6.     ~p             Assumption
7.     ~(~p | q)      Reiteration: 2
8.    ~p => ~(~p | q) Implication Introduction: 6, 7
9.    ~~p             Negation Introduction: 5, 8
10.   p               Negation Elimination: 9
11.   q               Implication Elimination: 1, 10
12.   ~p | q          Or Introduction: 11
13. ~(~p | q) => ~p | q        Implication Introduction: 2, 12
14.  ~(~p | q)                 Assumption
15. ~(~p | q) => ~(~p | q)     Implication Introduction: 14, 14
16. ~~(~p | q)                 Negation Introduction: 13, 15
17. ~p | q                     Negation Elimination: 16

Цель ~p | q завершено