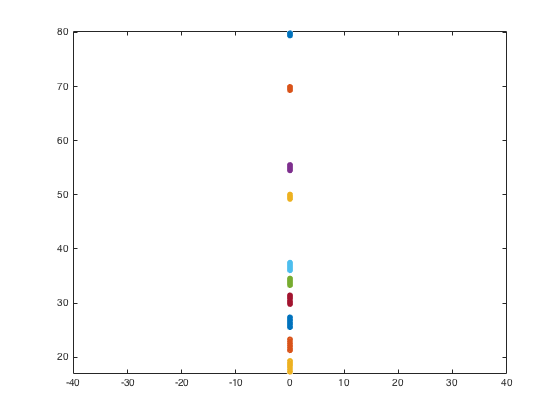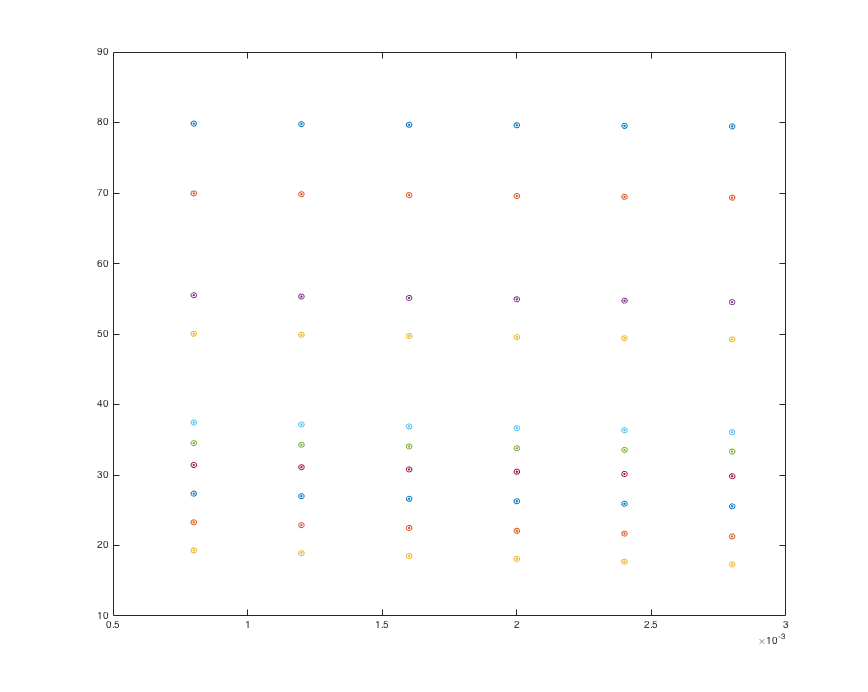Рисование окружностей вокруг точек на графике

Question

У меня есть две матрицы

timeline =  [0.0008    0.0012    0.0016    0.0020    0.0024    0.0028];

Origdata =

   79.8400   69.9390   50.0410   55.5082   34.5200   37.4486   31.4237   27.3532   23.2860   19.3039
   79.7600   69.8193   49.8822   55.3115   34.2800   37.1730   31.1044   26.9942   22.8876   18.9061
   79.6800   69.6996   49.7233   55.1148   34.0400   36.8975   30.7850   26.6352   22.4891   18.5084
   79.6000   69.5799   49.5645   54.9181   33.8000   36.6221   30.4657   26.2762   22.0907   18.1108
   79.5200   69.4602   49.4057   54.7215   33.5600   36.3467   30.1464   25.9173   21.6924   17.7133
   79.4400   69.3405   49.2469   54.5249   33.3200   36.0714   29.8271   25.5584   21.2941   17.3159

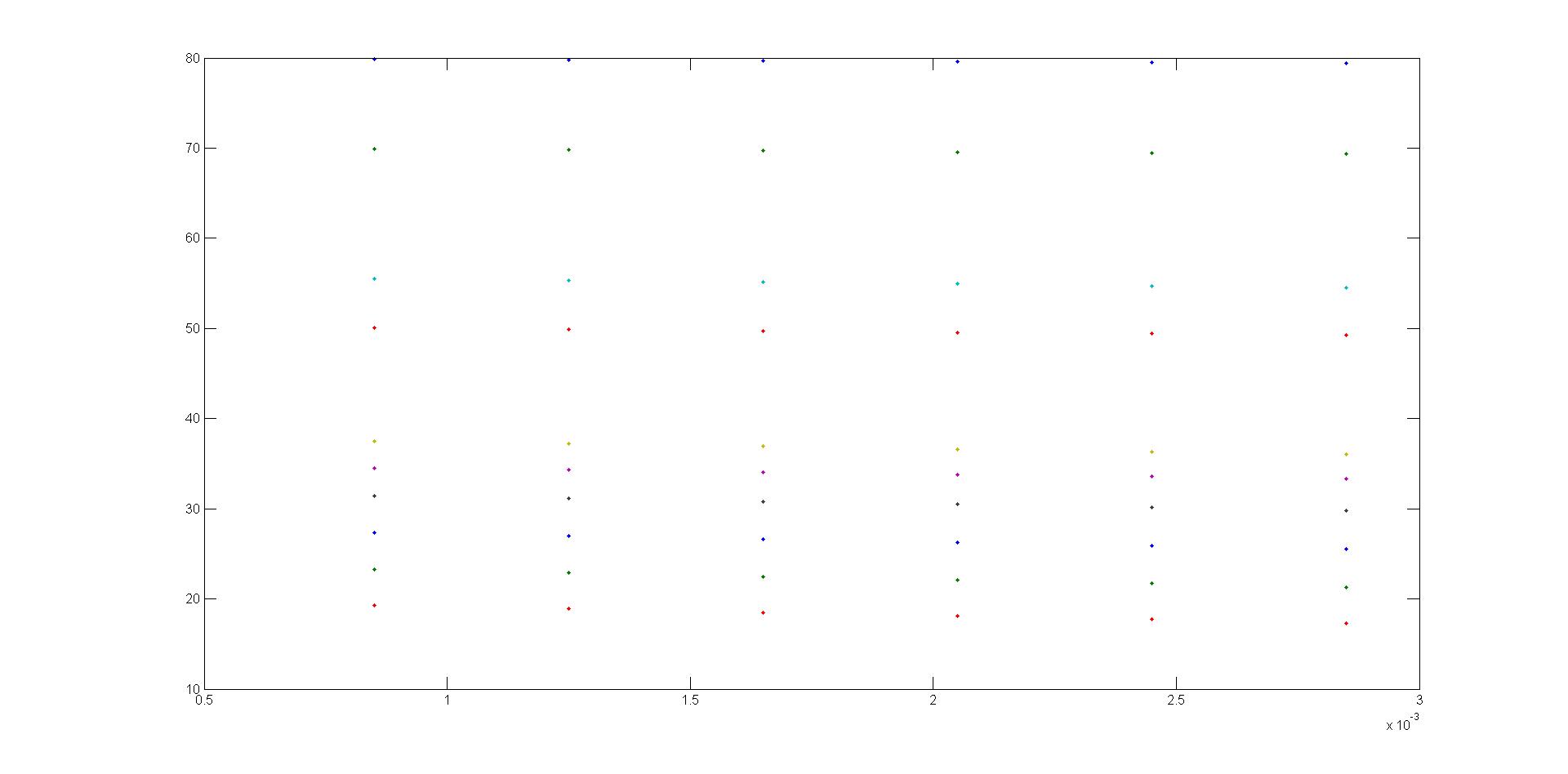
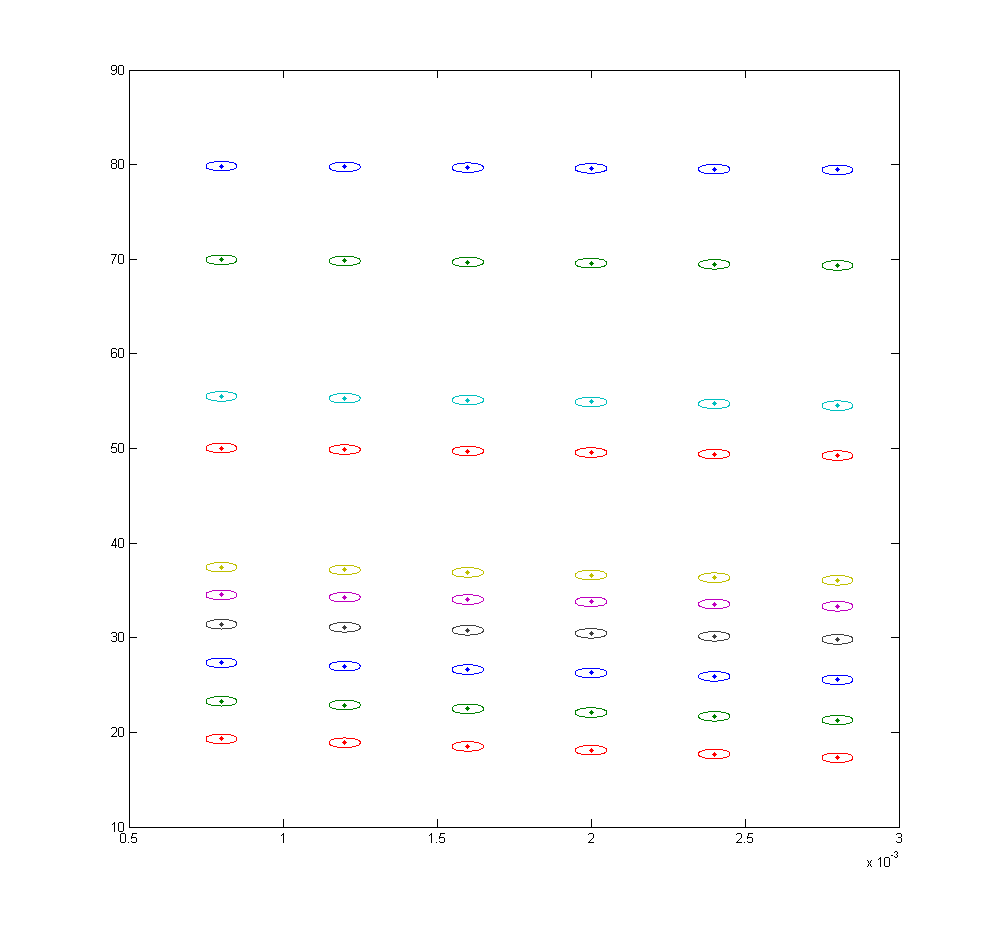
Когда я рисую их, я получаю график, как показано ниже.

plot(timeline, Origdata, '.');

Как нарисовать окружность с радиусом 0,3524 вокруг каждой точки? Этот радиус должен быть только относительно оси Y.

Answer 1

Вы можете сделать это легко, используя viscircles (для этого требуется набор инструментов для обработки изображений), однако я не думаю, что результат на самом деле соответствует вашим ожиданиям.

radius = 0.3524;
dots = plot(timeline, Origdata, '.');

hold on

for k = 1:numel(dots)
    plotdata = get(dots(k));
    centers = [plotdata.XData(:), plotdata.YData(:)];

    % Ensure the the colors match the original plot
    color = get(dots(k), 'Color');

    viscircles(centers, radius * ones(size(centers(:,1))), 'Color', color);
end

Причина, по которой это выглядит так, заключается в том, что ваши X-данные очень близки друг к другу относительно ваших y-данных и для того, чтобы круги выглядели как круги, я заставил масштабирование по осям x и y равным (axis equal)

редактировать

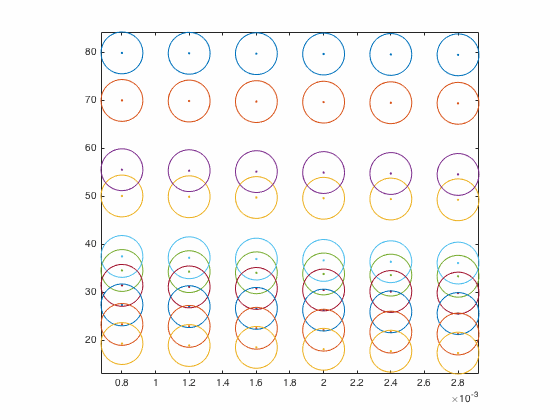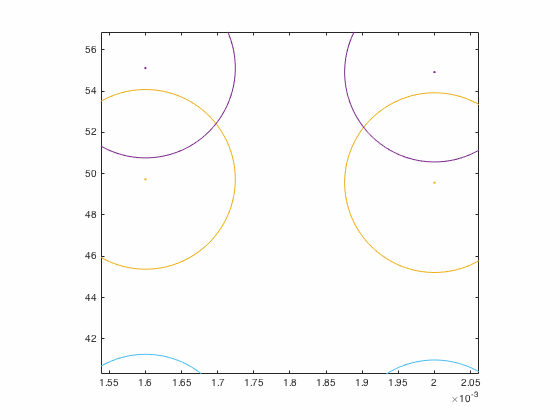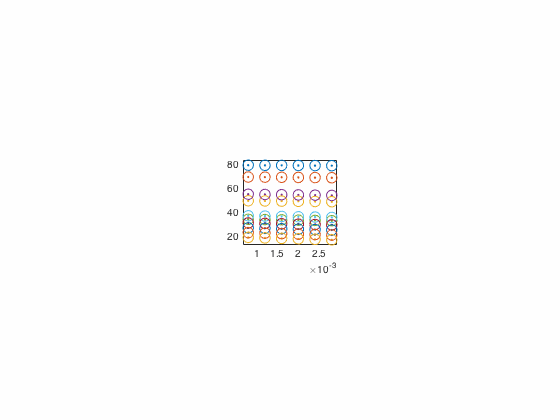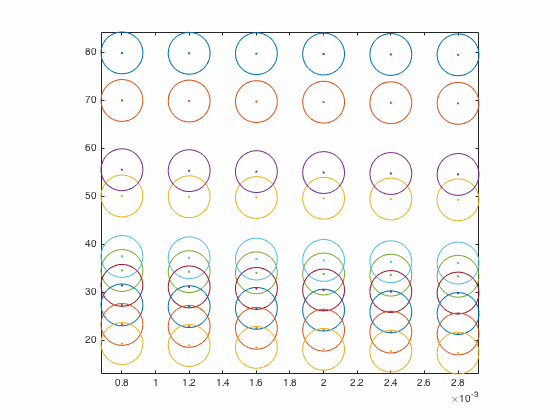
Если вы хотите только radius чтобы быть относительно оси y (расстояние), то нам нужно нарисовать эллипсы с радиусами x и y. Мы хотим масштабировать "x-radius", чтобы он выглядел как круг, независимо от вашего истинного соотношения сторон по осям, что-то подобное может сделать это.

Хитрость к приведенному ниже коду заключается в настройке соотношения сторон данных и графика (pbaspect а также daspect) к руководству. Это гарантирует, что соотношение сторон осей не изменяется во время масштабирования, изменения размера и т. Д., И гарантирует, что наши "круги" остаются круглыми.

dots = plot(timeline, Origdata, '.');

drawnow

% Force the aspect ratio to not change (keep the circles, as circles)
pbaspect('manual')
daspect('manual')

hold on

aspectRatio = daspect;

t = linspace(0, 2*pi, 100);
t(end+1) = NaN;

radius = 4.3524;

% Scale the radii for each axis
yradius = radius;
xradius = radius * aspectRatio(1)/aspectRatio(2);

% Create a circle "template" with a trailing NaN to disconnect consecutive circles
t = linspace(0, 2*pi, 100);
t(end+1) = NaN;
circle = [xradius*cos(t(:)), yradius*sin(t(:))];

for k = 1:numel(dots)
    x = get(dots(k), 'XData');
    y = get(dots(k), 'YData');
    color = get(dots(k), 'Color');

    % Center circle template at all points
    circles = arrayfun(@(x,y)bsxfun(@plus, [x,y], circle), x, y, 'uni', 0);
    circles = cat(1, circles{:});

    plot(circles(:,1), circles(:,2), 'Color', color)
end

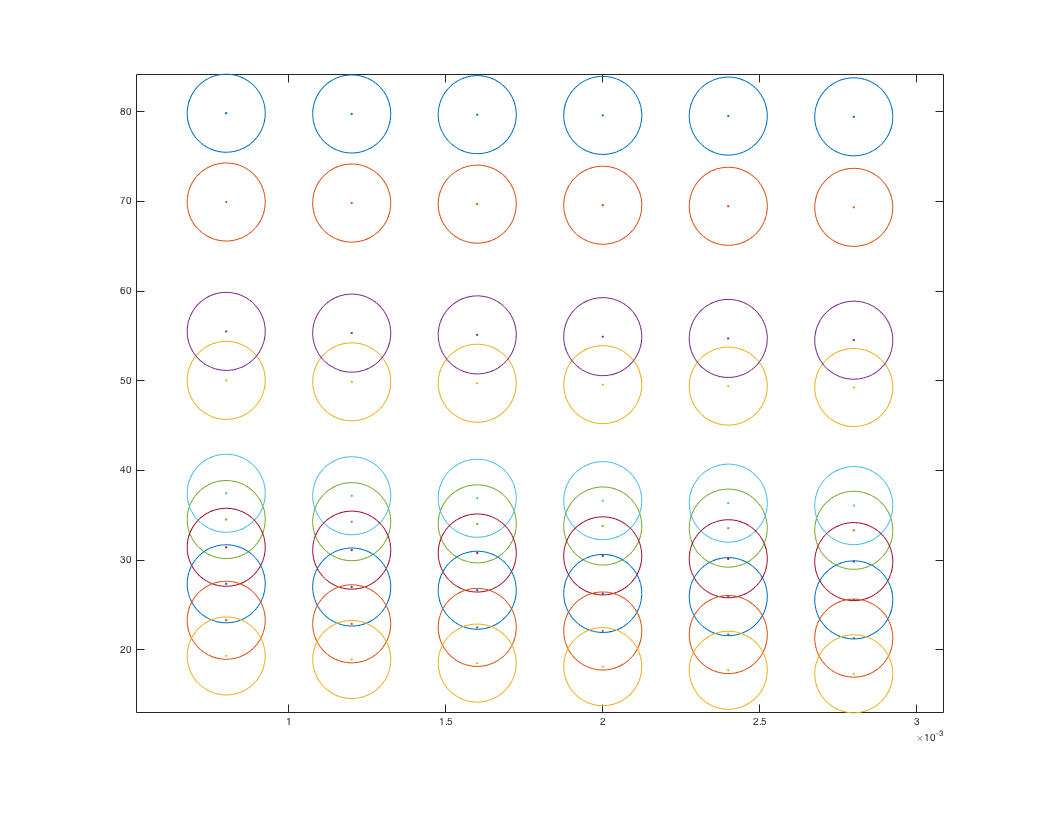
Просто для демонстрации, если мы увеличим радиус круга до 4,3524, мы сможем лучше видеть круги.

И это работает со всеми изменениями размера и т. Д.

Answer 2

Чтобы нарисовать круги в MATLAB, вы, очевидно, должны использовать rectangle функция;)

Как уже упоминалось в моем комментарии, размер 0.3524 не соответствует вашей оси, поэтому я выбрал разные размеры, чтобы круги на самом деле были видны. rx а также ry

timeline =  [0.0008    0.0012    0.0016    0.0020    0.0024    0.0028];
Orgidata =[79.8400   69.9390   50.0410   55.5082   34.5200   37.4486   31.4237   27.3532   23.2860   19.3039
   79.7600   69.8193   49.8822   55.3115   34.2800   37.1730   31.1044   26.9942   22.8876   18.9061
   79.6800   69.6996   49.7233   55.1148   34.0400   36.8975   30.7850   26.6352   22.4891   18.5084
   79.6000   69.5799   49.5645   54.9181   33.8000   36.6221   30.4657   26.2762   22.0907   18.1108
   79.5200   69.4602   49.4057   54.7215   33.5600   36.3467   30.1464   25.9173   21.6924   17.7133
   79.4400   69.3405   49.2469   54.5249   33.3200   36.0714   29.8271   25.5584   21.2941   17.3159];
ry=1;
rx=0.0001;
dots=plot(timeline, Orgidata , '.');
hold on
for ix=1:size(Orgidata ,1)
    for jx=1:size(Orgidata ,2)
        rectangle('Position',[timeline(ix)-(rx/2),Orgidata(ix,jx)-(ry/2),rx,ry],'Curvature',[1,1],'EdgeColor',get(dots(jx), 'Color'));
    end
end