Вычисление функции взаимной корреляции?

Question

В R, Я использую ccf или же acf вычислить функцию попарной взаимной корреляции, чтобы я мог выяснить, какой сдвиг дает мне максимальное значение. Судя по всему, R дает мне нормализованную последовательность значений. Есть ли что-то похожее в скрипте Python, или я должен сделать это, используя fft модуль? В настоящее время я делаю это следующим образом:

xcorr = lambda x,y : irfft(rfft(x)*rfft(y[::-1]))
x = numpy.array([0,0,1,1])
y = numpy.array([1,1,0,0])
print xcorr(x,y)

Answer 1

Для взаимной корреляции 1d-массивов используйте numpy.correlate.

Для 2d массивов используйте scipy.signal.correlate2d.

Существует также scipy.stsci.convolve.correlate2d.

Существует также matplotlib.pyplot.xcorr, основанный на numpy.correlate.

См. Этот пост в списке рассылки SciPy для некоторых ссылок на различные реализации.

Изменить: @user333700 добавил ссылку на тикет SciPy для этой проблемы в комментарии.

Answer 2

Если вы ищете быструю нормализованную взаимную корреляцию в одном или двух измерениях, я бы порекомендовал библиотеку openCV (см. http://opencv.willowgarage.com/wiki/ http://opencv.org/). Код взаимной корреляции, поддерживаемый этой группой, является самым быстрым, который вы найдете, и он будет нормализован (результаты между -1 и 1).

Хотя это библиотека C++, код поддерживается с помощью CMake и имеет привязки Python, так что доступ к функциям взаимной корреляции удобен. OpenCV также хорошо играет с NumPy. Если бы я хотел вычислить двумерную взаимную корреляцию, начиная с массивов-пустышек, я мог бы сделать это следующим образом.

import numpy
import cv

#Create a random template and place it in a larger image
templateNp = numpy.random.random( (100,100) )
image = numpy.random.random( (400,400) )
image[:100, :100] = templateNp

#create a numpy array for storing result
resultNp = numpy.zeros( (301, 301) )

#convert from numpy format to openCV format
templateCv = cv.fromarray(numpy.float32(template))
imageCv = cv.fromarray(numpy.float32(image))
resultCv =  cv.fromarray(numpy.float32(resultNp))

#perform cross correlation
cv.MatchTemplate(templateCv, imageCv, resultCv, cv.CV_TM_CCORR_NORMED)

#convert result back to numpy array
resultNp = np.asarray(resultCv)

Для одномерной взаимной корреляции создайте двумерный массив с формой, равной (N, 1). Хотя для преобразования в формат openCV требуется некоторый дополнительный код, ускорение по сравнению со scipy весьма впечатляет.

Answer 3

Я только что закончил писать свою собственную оптимизированную реализацию нормализованной взаимной корреляции для N-мерных массивов. Вы можете получить это отсюда.

Он будет рассчитывать взаимную корреляцию либо напрямую, используя scipy.ndimage.correlateили в частотной области, используя scipy.fftpack.fftn/ifftn в зависимости от того, что будет быстрее.

Answer 4

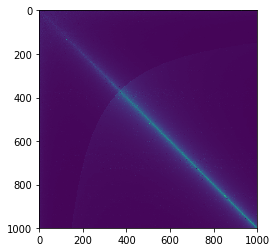
Для 1D массива, numpy.correlate быстрее чем scipy.signal.correlateпри разных размерах я вижу постоянный 5-кратный прирост производительности numpy.correlate, Когда два массива имеют одинаковый размер (яркая линия, соединяющая диагональ), разница в производительности становится еще более заметной (50x +).

# a simple benchmark
res = []
for x in range(1, 1000):
    list_x = []
    for y in range(1, 1000): 

        # generate different sizes of series to compare
        l1 = np.random.choice(range(1, 100), size=x)
        l2 = np.random.choice(range(1, 100), size=y)

        time_start = datetime.now()
        np.correlate(a=l1, v=l2)
        t_np = datetime.now() - time_start

        time_start = datetime.now()
        scipy.signal.correlate(in1=l1, in2=l2)
        t_scipy = datetime.now() - time_start

        list_x.append(t_scipy / t_np)
    res.append(list_x)
plt.imshow(np.matrix(res))

По умолчанию scipy.signal.correlate вычисляет несколько дополнительных чисел путем заполнения, и это может объяснить разницу в производительности.

>> l1 = [1,2,3,2,1,2,3]
>> l2 = [1,2,3]
>> print(numpy.correlate(a=l1, v=l2))
>> print(scipy.signal.correlate(in1=l1, in2=l2))

[14 14 10 10 14]
[ 3  8 14 14 10 10 14  8  3]  # the first 3 is [0,0,1]dot[1,2,3]