Каково общее количество возможных упорядоченных деревьев с N узлами?
Например, для N=3, мы можем легко найти, перечислив их все, но когда меня спрашивают о произвольном значении N, я сталкиваюсь с проблемой.
4 ответа
Если вы смотрите на двоичные деревья, то, как сказал Макдоуэлла, выберите (2n,n)/(n+1) (каталонское число).
Если вы смотрите на произвольные деревья, то это, вероятно, n. n^(n-2) = n^(n-1), но я не совсем уверен. Алгоритм Пруфера говорит нам, что существует n ^ (n-2) помеченных деревьев, и любой из узлов может стать корнем, поэтому мы получаем число n^(n-1).
Это описано в разделе Knuth Vol 1 (Искусство компьютерного программирования: фундаментальные алгоритмы). 2.3.4.4 Примерно на половине страницы математики вы можете выбрать "Выбрать" (2n, n) / (n + 1), и при поиске последовательности в Knuth найдется http://oeis.org/A000108
Вы можете сделать это, используя динамическое программирование:
Давайте fix element i as the root дерева. Теперь нам нужно знать how many different trees мы можем сформировать с the first (i-1) elements and the rest (n-i-1) elements,
Таким образом, мы следуем той же процедуре для этих двух подмассивов (i-1) а также (n-i-1) получить следующее повторение:
Формула:
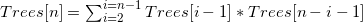
Латекс:
Деревья [N] и пространство;=& пространство;\sum_{я & пространство;=& пространство;2}^{я & пространство;=& пространство, п-1} и пространство, деревья [I-1]* Деревья [п-1]
Двоичные деревья (2n,n)/(n+1) (каталонское число) в качестве ответа Если обозначены деревья, чем n^(n-2) деревьев.