qqnorm и qqline в ggplot2
Скажем, есть линейная модель LM, что я хочу qq график остатков. Обычно я бы использовал базовую графику R:
qqnorm(residuals(LM), ylab="Residuals")
qqline(residuals(LM))
Я могу понять, как получить qqnorm часть графика, но я не могу управлять qqline:
ggplot(LM, aes(sample=.resid)) +
stat_qq()
Я подозреваю, что упускаю что-то довольно простое, но кажется, что должен быть легкий способ сделать это.
РЕДАКТИРОВАТЬ: Большое спасибо за решение ниже. Я изменил код (очень незначительно), чтобы извлечь информацию из линейной модели, чтобы график работал как удобный график в базовом графическом пакете R.
ggQQ <- function(LM) # argument: a linear model
{
y <- quantile(LM$resid[!is.na(LM$resid)], c(0.25, 0.75))
x <- qnorm(c(0.25, 0.75))
slope <- diff(y)/diff(x)
int <- y[1L] - slope * x[1L]
p <- ggplot(LM, aes(sample=.resid)) +
stat_qq(alpha = 0.5) +
geom_abline(slope = slope, intercept = int, color="blue")
return(p)
}
8 ответов
Следующий код даст вам сюжет, который вы хотите. Пакет ggplot, по-видимому, не содержит код для расчета параметров qqline, поэтому я не знаю, возможно ли достичь такого графика в (понятной) однострочной строке.
qqplot.data <- function (vec) # argument: vector of numbers
{
# following four lines from base R's qqline()
y <- quantile(vec[!is.na(vec)], c(0.25, 0.75))
x <- qnorm(c(0.25, 0.75))
slope <- diff(y)/diff(x)
int <- y[1L] - slope * x[1L]
d <- data.frame(resids = vec)
ggplot(d, aes(sample = resids)) + stat_qq() + geom_abline(slope = slope, intercept = int)
}
Вы также можете добавить доверительные интервалы / доверительные интервалы с помощью этой функции (части кода, скопированные из car:::qqPlot)
gg_qq <- function(x, distribution = "norm", ..., line.estimate = NULL, conf = 0.95,
labels = names(x)){
q.function <- eval(parse(text = paste0("q", distribution)))
d.function <- eval(parse(text = paste0("d", distribution)))
x <- na.omit(x)
ord <- order(x)
n <- length(x)
P <- ppoints(length(x))
df <- data.frame(ord.x = x[ord], z = q.function(P, ...))
if(is.null(line.estimate)){
Q.x <- quantile(df$ord.x, c(0.25, 0.75))
Q.z <- q.function(c(0.25, 0.75), ...)
b <- diff(Q.x)/diff(Q.z)
coef <- c(Q.x[1] - b * Q.z[1], b)
} else {
coef <- coef(line.estimate(ord.x ~ z))
}
zz <- qnorm(1 - (1 - conf)/2)
SE <- (coef[2]/d.function(df$z)) * sqrt(P * (1 - P)/n)
fit.value <- coef[1] + coef[2] * df$z
df$upper <- fit.value + zz * SE
df$lower <- fit.value - zz * SE
if(!is.null(labels)){
df$label <- ifelse(df$ord.x > df$upper | df$ord.x < df$lower, labels[ord],"")
}
p <- ggplot(df, aes(x=z, y=ord.x)) +
geom_point() +
geom_abline(intercept = coef[1], slope = coef[2]) +
geom_ribbon(aes(ymin = lower, ymax = upper), alpha=0.2)
if(!is.null(labels)) p <- p + geom_text( aes(label = label))
print(p)
coef
}
Пример:
Animals2 <- data(Animals2, package = "robustbase")
mod.lm <- lm(log(Animals2$brain) ~ log(Animals2$body))
x <- rstudent(mod.lm)
gg_qq(x)
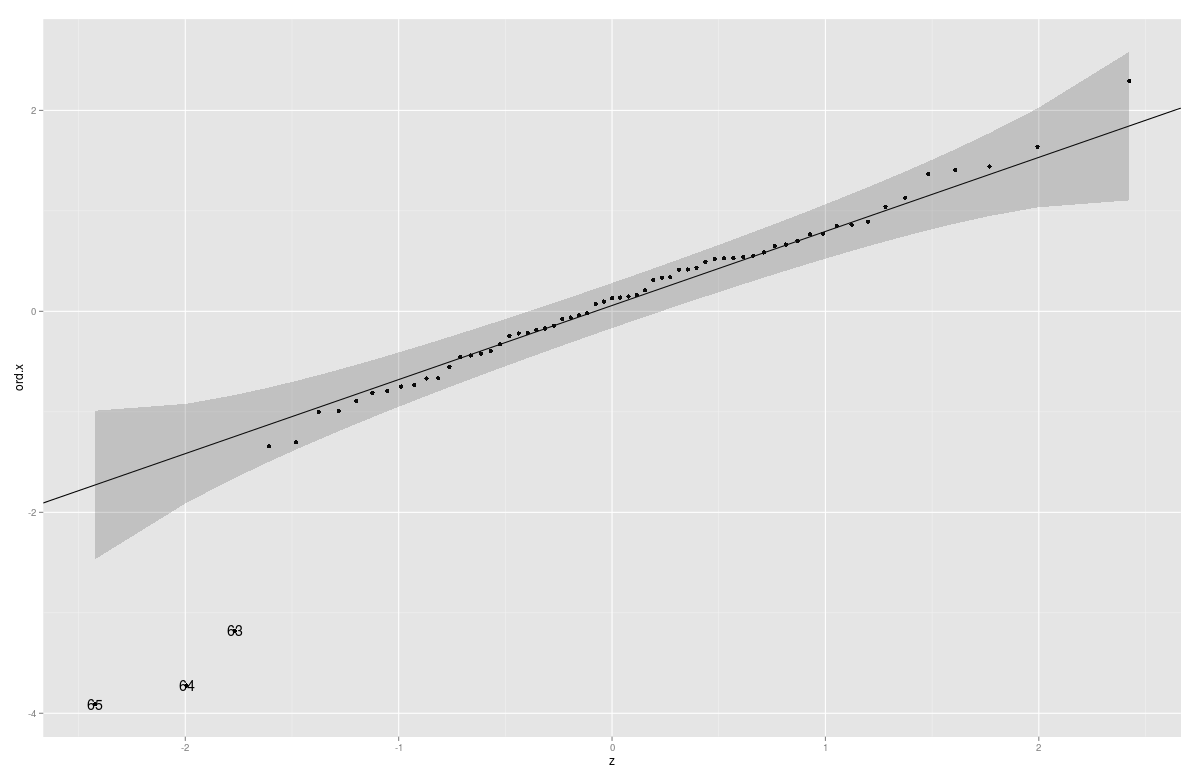
Начиная с версии 2.0, ggplot2 имеет хорошо документированный интерфейс для расширения; поэтому теперь мы можем легко написать новую статистику для qqline (что я сделал впервые, поэтому улучшения приветствуются):
qq.line <- function(data, qf, na.rm) {
# from stackru.com/a/4357932/1346276
q.sample <- quantile(data, c(0.25, 0.75), na.rm = na.rm)
q.theory <- qf(c(0.25, 0.75))
slope <- diff(q.sample) / diff(q.theory)
intercept <- q.sample[1] - slope * q.theory[1]
list(slope = slope, intercept = intercept)
}
StatQQLine <- ggproto("StatQQLine", Stat,
# http://docs.ggplot2.org/current/vignettes/extending-ggplot2.html
# https://github.com/hadley/ggplot2/blob/master/R/stat-qq.r
required_aes = c('sample'),
compute_group = function(data, scales,
distribution = stats::qnorm,
dparams = list(),
na.rm = FALSE) {
qf <- function(p) do.call(distribution, c(list(p = p), dparams))
n <- length(data$sample)
theoretical <- qf(stats::ppoints(n))
qq <- qq.line(data$sample, qf = qf, na.rm = na.rm)
line <- qq$intercept + theoretical * qq$slope
data.frame(x = theoretical, y = line)
}
)
stat_qqline <- function(mapping = NULL, data = NULL, geom = "line",
position = "identity", ...,
distribution = stats::qnorm,
dparams = list(),
na.rm = FALSE,
show.legend = NA,
inherit.aes = TRUE) {
layer(stat = StatQQLine, data = data, mapping = mapping, geom = geom,
position = position, show.legend = show.legend, inherit.aes = inherit.aes,
params = list(distribution = distribution,
dparams = dparams,
na.rm = na.rm, ...))
}
Это также обобщает распределение (точно так же, как stat_qq делает), и может использоваться следующим образом:
> test.data <- data.frame(sample=rnorm(100, 10, 2)) # normal distribution
> test.data.2 <- data.frame(sample=rt(100, df=2)) # t distribution
> ggplot(test.data, aes(sample=sample)) + stat_qq() + stat_qqline()
> ggplot(test.data.2, aes(sample=sample)) + stat_qq(distribution=qt, dparams=list(df=2)) +
+ stat_qqline(distribution=qt, dparams=list(df=2))
(К сожалению, поскольку qqline находится на отдельном слое, я не смог найти способ "повторно использовать" параметры распределения, но это должно быть лишь незначительной проблемой.)
Стандартная диагностика QQ для линейных моделей строит квантили стандартизированных остатков по сравнению с теоретическими квантилями N(0,1). @ Функция Питера ggQQ отображает остатки. Приведенный ниже фрагмент исправляет это и добавляет несколько косметических изменений, чтобы сделать сюжет более похожим на то, что можно получить из plot(lm(...)),
ggQQ = function(lm) {
# extract standardized residuals from the fit
d <- data.frame(std.resid = rstandard(lm))
# calculate 1Q/4Q line
y <- quantile(d$std.resid[!is.na(d$std.resid)], c(0.25, 0.75))
x <- qnorm(c(0.25, 0.75))
slope <- diff(y)/diff(x)
int <- y[1L] - slope * x[1L]
p <- ggplot(data=d, aes(sample=std.resid)) +
stat_qq(shape=1, size=3) + # open circles
labs(title="Normal Q-Q", # plot title
x="Theoretical Quantiles", # x-axis label
y="Standardized Residuals") + # y-axis label
geom_abline(slope = slope, intercept = int, linetype="dashed") # dashed reference line
return(p)
}
Пример использования:
# sample data (y = x + N(0,1), x in [1,100])
df <- data.frame(cbind(x=c(1:100),y=c(1:100+rnorm(100))))
ggQQ(lm(y~x,data=df))
С последней версией ggplot2 (>=3.0), новая функция stat_qq_line реализован ( https://github.com/tidyverse/ggplot2/blob/master/NEWS.md), и строку qq для остатков модели можно добавить с помощью:
library(ggplot2)
model <- lm(mpg ~ wt, data=mtcars)
ggplot(model, aes(sample = rstandard(model))) + geom_qq() + stat_qq_line()
rstandard(model) необходимо получить стандартизированный остаток. (кредит @jlhoward и @qwr)
Если вы получили сообщение "Ошибка в stat_qq_line(): не удалось найти функцию"stat_qq_line"", ваша версия ggplot2 устарела, и вы можете исправить ее, обновив пакет ggplot2: install.packages("ggplot2"),
Почему не следующее?
Учитывая некоторый вектор, скажем,
myresiduals <- rnorm(100) ^ 2
ggplot(data=as.data.frame(qqnorm( myresiduals , plot=F)), mapping=aes(x=x, y=y)) +
geom_point() + geom_smooth(method="lm", se=FALSE)
Но кажется странным, что мы должны использовать традиционную графическую функцию для поддержки ggplot2.
Разве мы не можем получить тот же эффект, начав с вектора, для которого мы хотим построить квантиль, а затем применив соответствующие функции stat и geom в ggplot2?
Хэдли Уикхем следит за этими постами? Может быть, он сможет показать нам лучший способ.
Вы могли бы украсть страницу у старожилов, которые делали это с обычной вероятностной бумагой. Внимательный взгляд на графику ggplot()+stat_qq() показывает, что опорная линия может быть добавлена с помощью geom_abline(), вот так
df <- data.frame( y=rpois(100, 4) )
ggplot(df, aes(sample=y)) +
stat_qq() +
geom_abline(intercept=mean(df$y), slope = sd(df$y))
ggplot2 v.3.0.0 теперь имеет qqline stat. Со страницы справки:
df <- data.frame(y = rt(200, df = 5))
p <- ggplot(df, aes(sample = y))
p + stat_qq() + stat_qq_line()
! ggplot2 v3.0.0 Пример статистики, эквивалентной qqnorm плюс аблайн] 1