Исследование государственного пространства в источнике NuSMV

Question

Я работаю над программой коррекции / синтеза проекта. Моя задача - получить трассировку ошибок (контрпример), найти ее в полном пространстве состояний и восстановить модель в этом месте. Я хочу реализовать это как расширение NuSMV.

Я отлаживал NuSMV, чтобы понять и изучить его исходный код. До сих пор я нашел свой путь к созданию BDD FSM (строка compile.c 520). Я пытаюсь найти способ пройти через bdd, чтобы получить программный доступ к пространству состояний и, таким образом, выполнить свою корректирующую работу над моделью. Я еще не смог понять функции рекурсивного исследования, которые NuSMV использует для проверки свойств через bdd fsm.

Я хотел бы знать, как я могу пройти через структуру BDD, чтобы я мог визуализировать ее с помощью инструментов, таких как точка. Я также хотел бы знать, были ли уже сделаны такие или смиларные визуализации (я искал, но оказался пустым). Во-вторых, я хотел бы проверить, является ли правильное направление, которое я выбрал, или есть ли лучший способ получить полное пространство состояний данной модели, и исследовать его, особенно в отношении контрпримеров, полученных через NuSMV.

Answer 1

Это ответ о способах работы с двоичными диаграммами решений (BDD) с использованием CUDD, отличных от NuSMV, поэтому сосредоточимся на второй части вопроса.

Что касается символьных алгоритмов исследования пространства состояний, то хорошим введением является статья "Алгоритмическая проверка спецификаций линейной темпоральной логики" Кестена, Пнуэли и Равива (ICALP '98, DOI: 10.1007 / BFb0055036), в которой рассматривается построение контрпримеров.

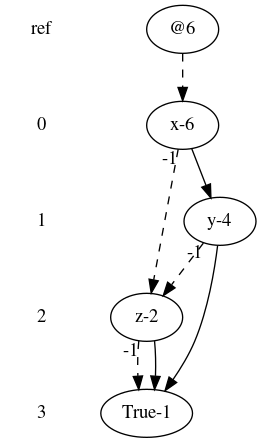
Одна из возможностей визуализации BDD - это работа на Python с использованием привязок Cython к CUDD:

from dd import cudd


def dump_pdf_cudd():
    bdd = cudd.BDD()
    bdd.declare('x', 'y', 'z')
    u = bdd.add_expr('(x /\ y) \/ ~ z')
    bdd.dump('foo.pdf', [u])


if __name__ == '__main__':
    dump_pdf_cudd()

Этот подход использует dd, который можно установить с помощью pip, с pip install dd. Документацию можно найти здесь. Глядя на (внутренний) модуль dd._abc также может быть информативным (это служит спецификацией; имя "abc" относится к абстрактным базовым классам в Python). (Чистый Python подходит для небольших задач, а CUDD полезен для более крупных).

К вопросу относятся два вида обходов:

1. обход графа BDD
2. обход графа, который имеет состояния как узлы и шаги как ребра.

Они обсуждаются отдельно ниже.

Обход графа BDD

При работе с BDD обход в глубину более распространен, чем в первую очередь на вдохе. Для интерфейсаdd.cudd а также dd.autoref такой обход:

from dd import autoref as _bdd


def demo_bdd_traversal():
    bdd = _bdd.BDD()
    bdd.declare('x', 'y')
    u = bdd.add_expr('x /\ y')
    print_bdd_nodes(u)


def print_bdd_nodes(u):
    visited = set()
    _print_bdd_nodes(u, visited)


def _print_bdd_nodes(u, visited):
    # terminal ?
    if u.var is None:
        print('terminal reached')
        return
    # non-terminal
    # already visited ?
    if u in visited:
        return
    # recurse
    v = u.low
    w = u.high
    # DFS pre-order
    print('found node {u}'.format(u=u))
    _print_bdd_nodes(v, visited)
    # DFS in-order
    print('back to node {u}'.format(u=u))
    _print_bdd_nodes(w, visited)
    # DFS post-order
    print('leaving node {u}'.format(u=u))
    # memoize
    visited.add(u)


if __name__ == '__main__':
    demo_bdd_traversal()

Дополненные края также необходимо учитывать при работе с BDD (с использованием CUDD или подобных библиотек). Атрибутu.negated предоставляет эту информацию.

Функция dd.bdd.copy_bdd- это чистый Python-пример обхода BDD. Эта функция управляет BDD напрямую через "низкоуровневый" интерфейс, который обернутdd.autoref выглядеть так же, как dd.cudd.

Обход графа состояний

Сценарий dd/examples/reachability.py показывает, как вычислить, из каких состояний можно достичь заданного набора состояний за конечное число шагов.

Пакет omega удобнее чем ddдля разработки алгоритмов на основе BDD, связанных с поведением системы. Сценарий omega/examples/reachability_solver демонстрирует вычисление достижимости с использованием omega.

Базовый пример прямой достижимости с использованиемomega == 0.3.1 следует:

from omega.symbolic import temporal as trl
from omega.symbolic import prime as prm


def reachability_example():
    """How to find what states are reachable."""
    aut = trl.Automaton()
    vrs = dict(
        x=(0, 10),
        y=(3, 50))
    aut.declare_variables(**vrs)
    aut.varlist = dict(
        sys=['x', 'y'])
    aut.prime_varlists()
    s = r'''
        Init ==
            /\ x = 0
            /\ y = 45

        Next ==
            /\ (x' = IF x < 10 THEN x + 1 ELSE 0)
            /\ (y' = IF y > 5 THEN y - 1 ELSE 45)
        '''
    aut.define(s)
    init = aut.add_expr('Init', with_ops=True)
    action = aut.add_expr('Next', with_ops=True)
    reachable = reachable_states(init, action, vrs, aut)
    n = aut.count(reachable, care_vars=['x', 'y'])
    print('{n} states are reachable'.format(n=n))


def reachable_states(init, action, vrs, aut):
    """States reachable by `action` steps, starting from `init`."""
    operator = lambda y: image(y, action, vrs, aut)
    r = least_fixpoint(operator, init)
    assert prm.is_state_predicate(r)
    return r


def image(source, action, vrs, aut):
    """States reachable from `source` in one step that satisfies `action`."""
    u = source & action
    u = aut.exist(vrs, u)
    return aut.replace_with_unprimed(vrs, u)


def least_fixpoint(operator, target):
    """Least fixpoint of `operator`, starting from `target`."""
    y = target
    yold = None
    while y != yold:
        yold = y
        y |= operator(y)
    return y


if __name__ == '__main__':
    reachability_example()

Сравнение omega с dd:

• omega поддерживает переменные и константы, а также целочисленные значения для них (соответствующий модуль omega.symbolic.temporal). Переменные представляют изменения состояния, напримерx а также x'. Константы остаются неизменными в зависимости от поведения системы.

• dd поддерживает только переменные с логическими значениями (omega использует логические переменные для представления целочисленных переменных и, таким образом, представляет предикаты как BDD через dd; битбластинг выполняется в модуле omega.logic.bitvector).

Несколько операторов фиксированных точек реализованы в omega.symbolic.fixpoint. Эти операторы могут использоваться для проверки модели или временного синтеза. Модульomega.logic.pastвключает переводы темпоральных операторов, которые имеют отношение к символьной проверке модели (также известные как временные тестеры).

Документация omegaможно найти здесь.

Дальнейшие комментарии

Выше я использовал термин "шаг" для обозначения пары последовательных состояний, которые представляют изменение состояния, разрешенное спецификацией. Язык и шаги TLA+, гибкие и жесткие переменные, а также другие полезные концепции описаны в книге Лесли Лэмпорта " Спецификация систем".

Набор программного обеспечения для формальной проверки приведен по адресу https://github.com/johnyf/tool_lists/.

По моему опыту, работа на уровне Python с использованием только менеджера BDD на уровне C - это эффективный подход, который приводит к читаемому коду и более четким алгоритмам.