Координатный спуск в Python

Question

Я хочу внедрить Coordinate Descent в Python и сравнить результат с Gradient Descent. Я написал код. Но это не работает хорошо. GD, возможно, в порядке, но CD не хорош.

Это ссылка на Координатный спуск. --- ССЫЛКА

И я ожидал, что этот результат Gradient Descent vs Coordinate Descent

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(10, 100, 1000)
y = np.linspace(10, 100, 1000)

def func(x, y, param):
    return param[0] * x + param[1] * y

def costf(X, y, param):
    return np.sum((X.dot(param) - y) ** 2)/(2 * len(y))

z = func(x, y, [5, 8]) + np.random.normal(0., 10.)
z = z.reshape(-1, 1)

interc = np.ones(1000)
X = np.concatenate([interc.reshape(-1, 1), x.reshape(-1, 1), y.reshape(-1, 1)], axis=1)

#param = np.random.randn(3).T
param = np.array([2, 2, 2])

def gradient_descent(X, y, param, eta=0.01, iter=100):
    cost_history = [0] * iter

    for iteration in range(iter):
        h = X.dot(param)
        loss = h - y
        gradient = X.T.dot(loss)/(2 * len(y))
        param = param - eta * gradient
        cost = costf(X, y, param)
        #print(cost)
        cost_history[iteration] = cost

    return param, cost_history


def coordinate_descent(X, y, param, iter=100):
    cost_history = [0] * iter

    for iteration in range(iter):
        for i in range(len(param)):
            dele = np.dot(np.delete(X, i, axis=1), np.delete(param, i, axis=0))
            param[i] = np.dot(X[:,i].T, (y - dele))/np.sum(np.square(X[:,i]))
            cost = costf(X, y, param)
            #print(cost)
            cost_history[iteration] = cost

    return param, cost_history


ret, xret = gradient_descent(X, z, param)
cret, cxret = coordinate_descent(X, z, param)

plt.plot(range(len(xret)), xret, label="GD")
plt.plot(range(len(cxret)), cxret, label="CD")
plt.legend()
plt.show()

Заранее спасибо.

Answer 1

Я не эксперт по оптимизации. Вот только некоторые советы.

Ваш код выглядит довольно хорошо для меня, за исключением того, что

1. следующие две строки кажутся неправильными

loss = h - y

param[i] = np.dot(X[:,i].T, (y - dele))/np.sum(np.square(X[:,i]))

Вы изменили у в (n_samples, 1) с z = z.reshape(-1, 1), в то время как h а также dele имеет форму (n_samples,), Это приводит к (n_samples, n_samples) Матрица, которую я думаю, не то, что вы хотели.

2. Ваши данные могут быть не очень хороши для целей тестирования. Это не значит, что это не сработает, но вам, возможно, понадобятся некоторые усилия, чтобы настроить скорость обучения / количество итераций.

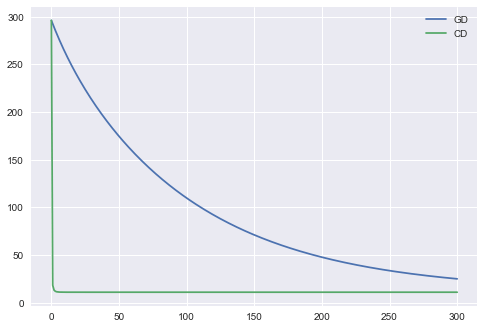
Я попробовал ваш код в наборе данных Бостона, вывод выглядит следующим образом.

код

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

#  boston house-prices dataset
data = load_boston()
X, y = data.data, data.target

X = StandardScaler().fit_transform(X)  # for easy convergence
X = np.hstack([X, np.ones((X.shape[0], 1))])

param = np.zeros(X.shape[1])

def gradient_descent(X, y, param, eta=0.01, iter=300):
    cost_history = [0] * (iter+1)
    cost_history[0] = costf(X, y, param)  # you may want to save initial cost

    for iteration in range(iter):
        h = X.dot(param)
        loss = h - y.ravel()
        gradient = X.T.dot(loss)/(2 * len(y))
        param = param - eta * gradient
        cost = costf(X, y, param)
        #print(cost)
        cost_history[iteration+1] = cost

    return param, cost_history

def coordinate_descent(X, y, param, iter=300):
    cost_history = [0] * (iter+1)
    cost_history[0] = costf(X, y, param)

    for iteration in range(iter):
        for i in range(len(param)):
            dele = np.dot(np.delete(X, i, axis=1), np.delete(param, i, axis=0))
            param[i] = np.dot(X[:,i].T, (y.ravel() - dele))/np.sum(np.square(X[:,i]))
            cost = costf(X, y, param)
            cost_history[iteration+1] = cost

    return param, cost_history

ret, xret = gradient_descent(X, y, param)
cret, cxret = coordinate_descent(X, y, param.copy())

plt.plot(range(len(xret)), xret, label="GD")
plt.plot(range(len(cxret)), cxret, label="CD")
plt.legend()

Если это то, что вы хотите, вы можете попробовать проверить некоторые другие данные. Только будьте осторожны, что даже реализация верна, вам все еще нужно настроить гиперпараметры, чтобы получить хорошую сходимость.