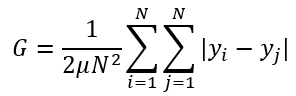Формула вычисления коэффициента Джини в fastgini

Question

Я использую fastgini пакет для Stata ( https://ideas.repec.org/c/boc/bocode/s456814.html).

Я знаком с классической формулой для коэффициента Джини, приведенной, например, в Karagiannis & Kovacevic (2000) ( http://onlinelibrary.wiley.com/doi/10.1111/1468-0084.00163/abstract)

Формула I:

Здесь G - коэффициент Джини, µ - среднее значение распределения, N - размер выборки, а y_i - доход i-й единицы выборки. Следовательно, коэффициент Джини вычисляет разницу между всеми доступными парами доходов в данных и вычисляет сумму всех абсолютных разниц.

Затем это общее число нормализуется путем деления его на среднеквадратичное значение дохода населения (и умноженное на два?).

Коэффициент Джини находится в диапазоне от 0 до 1, где 0 означает совершенное равенство (все люди зарабатывают одинаково), а 1 означает максимальное неравенство (1 человек получает весь доход в стране).

Тем не менее fastgini пакет относится к другой формуле ( http://fmwww.bc.edu/repec/bocode/f/fastgini.html):

Формула II:

fastgini uses formula:
                  i=N      j=i
                  SUM W_i*(SUM W_j*X_j - W_i*X_i/2)
                  i=1      j=1
      G = 1 - 2* ----------------------------------
                       i=N             i=N
                       SUM W_i*X_i  *  SUM W_i
                       i=1             i=1

где наблюдения отсортированы в порядке возрастания X.

Здесь W, кажется, вес, который я не использую, поэтому он должен быть 1 (?). Я не уверен, что формула I и формула II одинаковы. Абсолютных различий нет, и результат вычитается из 1 в формуле II. Я пытался преобразовать уравнения, но я не получаю дальше.

Может ли кто-нибудь дать мне подсказку, эквивалентны ли оба способа вычисления (формула I + формула II)?