Аппроксимация многоугольника с помощью круга

Question

Ну, аппроксимация круга с многоугольником и история Пифагора могут быть хорошо известны. А как же наоборот?

У меня есть несколько полигонов, которые должны быть кругами. Однако из-за ошибок измерений их нет. Итак, я ищу круг, который лучше всего "приближает" данный многоугольник.

На следующем рисунке мы видим два разных примера.

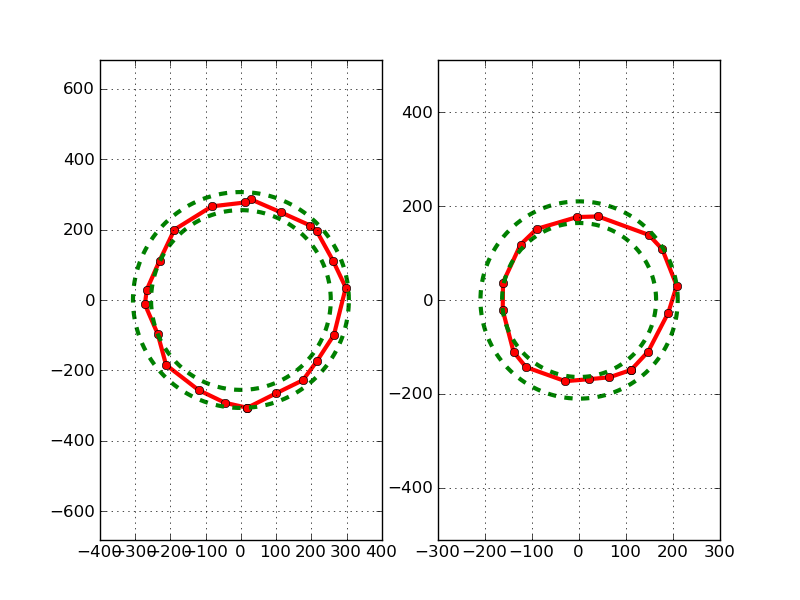
Моим первым ансацем было найти максимальное расстояние между точками и центром, а также минимальное. Круг, который мы ищем, может быть где-то посередине.

Есть ли какой-нибудь алгоритм для этой проблемы?

Answer 1

Я хотел бы использовать scipy лучше всего "подогнать" круг по моим точкам. Вы можете получить начальную точку для центра и радиуса с помощью простого вычисления центра масс. Это хорошо работает, если точки равномерно распределены по кругу. Если это не так, как в примере ниже, это все же лучше, чем ничего!

Функция подгонки проста, потому что круг прост. Вам нужно только найти радиальное расстояние от круга прилегания к вашим точкам, поскольку касательная (радиальная) поверхность всегда будет наилучшим образом.

import numpy as np
from scipy.spatial.distance import cdist
from scipy.optimize import fmin
import scipy

# Draw a fuzzy circle to test
N = 15
THETA = np.random.random(15)*2*np.pi
R     = 1.5 + (.1*np.random.random(15) - .05)
X = R*np.cos(THETA) + 5
Y = R*np.sin(THETA) - 2

# Choose the inital center of fit circle as the CM
xm = X.mean()
ym = Y.mean()

# Choose the inital radius as the average distance to the CM
cm = np.array([xm,ym]).reshape(1,2)
rm = cdist(cm, np.array([X,Y]).T).mean()

# Best fit a circle to these points
def err((w,v,r)):
    pts = [np.linalg.norm([x-w,y-v])-r for x,y in zip(X,Y)]
    return (np.array(pts)**2).sum()

xf,yf,rf = scipy.optimize.fmin(err,[xm,ym,rm])  

# Viszualize the results
import pylab as plt
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

# Show the inital guess circle
circ = plt.Circle((xm, ym), radius=rm, color='y',lw=2,alpha=.5)
ax.add_patch(circ)

# Show the fit circle
circ = plt.Circle((xf, yf), radius=rf, color='b',lw=2,alpha=.5)
ax.add_patch(circ)

plt.axis('equal')
plt.scatter(X,Y)
plt.show()

Answer 2

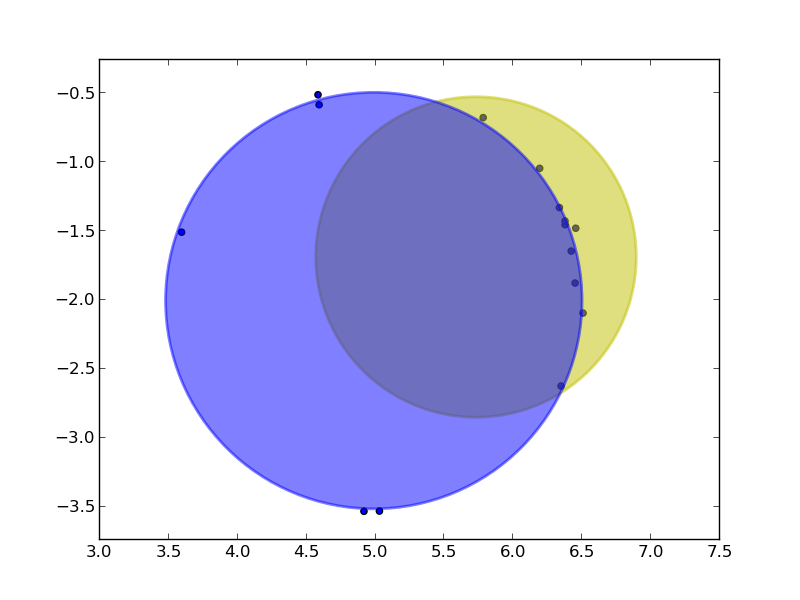
Возможно, простым алгоритмом было бы, во-первых, вычислить центр тяжести точек (при условии, что они обычно приблизительно равномерно разнесены). Это центр круга. Как только у вас есть это, вы можете рассчитать средний радиус точек, давая радиус круга.

Более сложным ответом может быть простая минимизация, где вы минимизируете сумму расстояний точек до края круга (или расстояния в квадрате).

Answer 3

Эта проблема может быть такой же, как проблема наименьшего круга.

Но так как у вас есть ошибки измерения, которые могут включать выбросы, тогда RANSAC является хорошим вариантом. См. http://cs.gmu.edu/~kosecka/cs482/lect-fitting.pdf для обзора метода (а также других базовых методов) в http://www.asl.ethz.ch/education/master/info-process-rob/Hough-Ransac.pdf есть больше информации, посвященной подгонке круга.

Answer 4

Существует два различных алгоритма O(n) для определения наименьшего круга, который вы рисуете, который охватывает серию точек на задаче наименьшего круга на странице википедии. Отсюда должно быть довольно легко нарисовать второй круг, просто определите центр круга, который вы нашли ранее, и найдите точку, ближайшую к этой точке. Радиус второго круга таков.

Это может быть не совсем то, что вы хотите, но я бы так начал.

Answer 5

Это довольно легко найти некоторое приближение:

def find_circle_deterministically(x,y):
    center = x.mean(), y.mean()
    radius = np.sqrt((x-center[0])**2 + (y-center[1])**2).mean()
    return center, radius

Объяснено: поместите центр круга в среднее значение x и среднее значение y ваших точек. Затем для каждой точки определите расстояние до центра и возьмите среднее значение по всем точкам. Это твой радиус.

Этот полный сценарий:

import numpy as np
import matplotlib.pyplot as plt

n_points = 10
radius = 4
noise_std = 0.3

angles = np.linspace(0,2*np.pi,n_points,False)
x = np.cos(angles) * radius
y = np.sin(angles) * radius
x += np.random.normal(0,noise_std,x.shape)
y += np.random.normal(0,noise_std,y.shape)

plt.axes(aspect="equal")
plt.plot(x,y,"bx")

def find_circle_deterministically(x,y):
    center = x.mean(), y.mean()
    radius = np.sqrt((x-center[0])**2 + (y-center[1])**2).mean()
    return center, radius

center, radius2 = find_circle_deterministically(x,y)
angles2 = np.linspace(0,2*np.pi,100,True)
x2 = center[0] + np.cos(angles2) * radius2
y2 = center[1] + np.sin(angles2) * radius2
plt.plot(x2,y2,"r-")

plt.show()

производит этот сюжет:

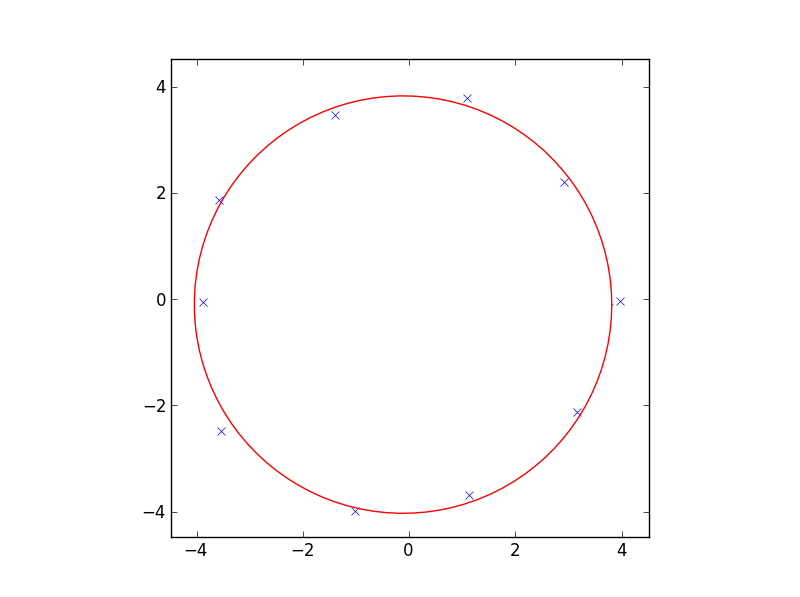
Это будет хорошо работать, так как у вас есть полигоны с ошибками измерений. Если ваши точки не примерно одинаково распределены по углам [0,2pi[будет плохо работать.

В целом, вы можете использовать оптимизацию.