Верхняя граница окраски графа
Википедия утверждает для раскраски графа следующую верхнюю границу:
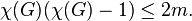
Но я не понимаю, почему это так. Дать. Информация мне неясна.
Кто-то, кто может мне помочь?
1 ответ
здесь так ясно, кстати, предложение
В оптимальной раскраске должен быть хотя бы один из m ребер графа между каждой парой цветовых классов
Я сломаю это и сделаю каждую часть более ясной.
В оптимальной раскраске: это означает, что вы нашли раскраску в графе, что вы не можете уменьшить ее больше цвета, и если вы уменьшите один цвет, будет два похожих цветовых соседа.
должен быть хотя бы один из графа
mкрая между каждой парой цветовых классов: рассмотрим оптимальную раскраску из первой части, например, было два цветаAа такжеBчто нет границы междуAцветные узлы иBцветные узлы (в отличие от этого утверждения), то мы могли бы изменить цвета всехAцветные узлы для окраскиB, но это противоречие с первым утверждением.Из первых двух утверждений у нас есть формула:
- у нас есть
X(G)(X(G) - 1)/2пары цветов в этой раскраске. - между этими парами есть хотя бы одно ребро.
- так что у нас есть
X(G)(X(G) - 1) /2меньше чем равноmитак имеем:
- у нас есть