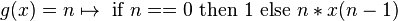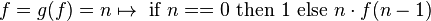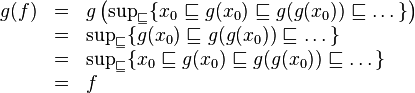Денотационная семантика, доказывающая, что итерация с фиксированной точкой приводит к наименьшей фиксированной точке

Question

Я работаю над разделом wikibook на Haskell, посвященном денотационной семантике, и застрял в этом упражнении:

Докажите, что фиксированная точка, полученная итерацией с фиксированной точкой, начиная с также наименьшее, что оно меньше, чем любая другая фиксированная точка. (Подсказка: является наименьшим элементом нашего cpo и g является монотонным).

Где следующие утверждения определяют суть понятий, приводящих к упражнению (я думаю):

где f - факториальная функция, и показано, что она является фиксированной точкой g, учитывая, что g непрерывна.

Я думаю, что в основном понимаю ту часть, где показано, что g(f) = f, но я не знаю, что делать с этим упражнением. Из того, что я понимаю, факториальная функция f является наименее фиксированной точкой (причем наименьшая из 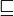оператор), но мне не совсем понятно, что значит (интуитивно) сравнивать функции с 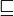не говоря уже о том, как бы я нашел фиксированные точки, отличные от наименее фиксированной точки, показанной в примере.

Я это понимаю 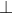меньше, чем все остальное, и я понимаю, что, поскольку g(x) является монотонным, если применить его к двум вещам, где одно меньше другого, результаты все равно будут подчиняться этому порядку.

Я думаю, что я бы начал доказательство с принятия некоторой функции f 'и предположив, , Если это так, то через монотонное свойство g я могу показать, что 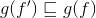, Если я тогда смогу показать, что обязательно g(f') = g(f) или f' = f, я думаю, что доказательство закончено, но я понятия не имею, как это показать.

Answer 1

Позволять x быть верхним / наименьшим верхним пределом последовательности bot, g(bot), g(g(bot)), ..., Позволять y быть любой фиксированной точкой g (Монотонный). Мы хотим доказать это x <= y,

По индукции по количеству итераций легко увидеть, что каждый элемент в последовательности <= y, Действительно, это тривиально bot, и если z является <= y по монотонности получаем g(z) <= g(y) = y,

Так, y верхняя граница последовательности. Но x наименее, так x <= y, QED.