Полиномиальные данные и R's glm()

Question

Как вы можете заставить R glm () соответствовать полиномиальным данным? Я пробовал несколько итераций 'family=AAA(link="BBB") ", но мне кажется, что тривиальные прогнозы не совпадают.

Например, пожалуйста, помогите с R GLM, чтобы соответствовать полиномиальным данным

x=seq(-6,6,2)
y=x*x
parabola=data.frame(x,y)
plot(parabola)
model=glm(y~x,dat=parabola)
test=data.frame(x=seq(-5,5,2))
test$y=predict(model,test)
plot(test)

График (парабола) выглядит так, как ожидалось, но я могу найти заклинание glm (), которое сделает график (тест) параболическим.

Answer 1

Я думаю, что вам нужно сделать шаг назад и начать думать о модели и о том, как вы представляете это в R. В вашем примере y является квадратичной функцией x, так что вам нужно включить x а также x^2 в формуле модели, т. е. в качестве предикторов вы должны оценить влияние x а также x^2 на ответ дали данные в руки.

Если y является гауссовым, зависит от модели, то вы можете сделать это с lm() и либо

y ~ x + I(x^2)

или же

y ~ poly(x, 2)

В первом мы заключаем квадратный член в I() как ^ Оператор имеет особое значение (не его математическое значение) в формуле R-модели. Последняя версия дает ортогональные полиномы и, следовательно, x а также x^2 Термины не будут коррелированными, что может помочь с подгонкой, однако в некоторых случаях интерпретация коэффициентов сложнее poly(),

Собирая все вместе, мы имеем (обратите внимание, что я добавляю случайную ошибку к y чтобы не предсказать это совершенно, поскольку пример, который я использую, более распространен в реальности):

x <- seq(-6 ,6 ,2)
y <- x^2 + rnorm(length(x), sd = 2)
parabola <- data.frame(x = x, y = y)

mod <- lm(y ~ poly(x, 2), data = parabola)

plot(parabola)
lines(fitted(mod) ~ x, data = parabola, col = "red")

Сюжет произведен:

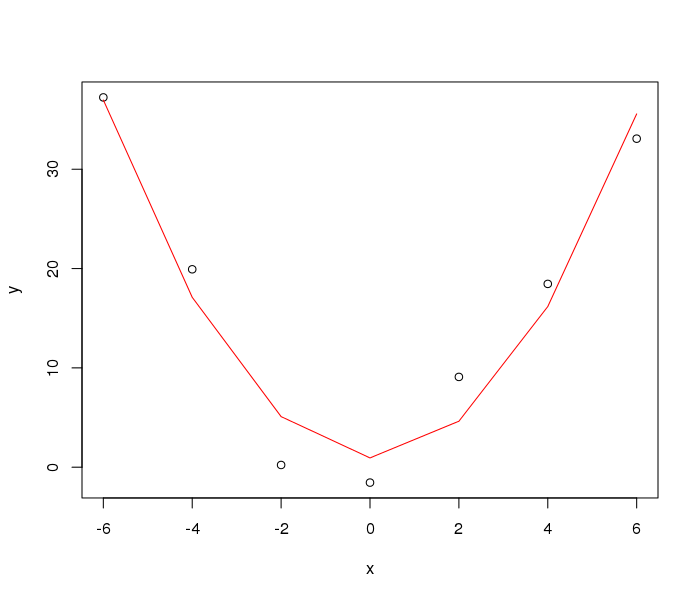
Дополнительным вопросом является ли y такое гауссов? Если y не может быть отрицательным (то есть счет) и / или дискретным, моделирование с использованием lm() будет неправильно. Это где glm() может прийти, по которому вы могли бы соответствовать кривой без необходимости x^2 (хотя если данные действительно являются параболой, то x сам по себе не подходит для ответа), поскольку существует явное преобразование данных из линейного предиктора в масштаб ответа.

Лучше подумать о свойствах данных и типе модели, которую вы хотите подогнать, а затем выстроить степень полинома в рамках этой модели, а не пытаться использовать различные заклинания, чтобы просто изогнуть данные.

Answer 2

Матч сейчас идеальный. Немного более интересная парабола:

x=seq(-16,16,2)
y= 4*x*x + 10*x + 6
parabola=data.frame(x,y)
plot(parabola)
model=lm(y~poly(x,2),dat=parabola)
summary(model)
test=data.frame(x=seq(-15,15,2))
test$y=predict(model,test)
points(test,pch=3)

Любитель (как и я) может ожидать, что коэффициенты модели будут (4,10,6) соответствовать 4*x*x + 10*x + 6

Call:
lm(formula = y ~ poly(x, 2), data = parabola)

Residuals:
       Min         1Q     Median         3Q        Max 
-3.646e-13 -8.748e-14 -3.691e-14  4.929e-14  6.387e-13 

Coefficients:
             Estimate Std. Error   t value Pr(>|t|)    
(Intercept) 3.900e+02  5.192e-14 7.511e+15   <2e-16 ***
poly(x, 2)1 4.040e+02  2.141e-13 1.887e+15   <2e-16 ***
poly(x, 2)2 1.409e+03  2.141e-13 6.581e+15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.141e-13 on 14 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:      1 
F-statistic: 2.343e+31 on 2 and 14 DF,  p-value: < 2.2e-16

Почему коэффициенты были бы (390,404,1409)?