Создание фильтра низких частот в SciPy - понимание методов и единиц

Question

Я пытаюсь отфильтровать шумовой сигнал сердечного ритма с помощью Python. Поскольку частота сердечных сокращений никогда не должна быть около 220 ударов в минуту, я хочу отфильтровать весь шум выше 220 ударов в минуту. Я конвертировал 220/ мин в 3,66666666 герц, а затем конвертировал этот герц в рад / с, чтобы получить 23,0383461 рад / сек.

Частота дискретизации чипа, принимающего данные, составляет 30 Гц, поэтому я преобразовал его в рад / с, чтобы получить 188,495559 рад / с.

Посмотрев некоторые вещи в Интернете, я нашел несколько унций для полосового фильтра, которые я хотел превратить в низкочастотный. Вот ссылка на код полосы пропускания, поэтому я конвертировал ее так:

from scipy.signal import butter, lfilter
from scipy.signal import freqs

def butter_lowpass(cutOff, fs, order=5):
    nyq = 0.5 * fs
    normalCutoff = cutOff / nyq
    b, a = butter(order, normalCutoff, btype='low', analog = True)
    return b, a

def butter_lowpass_filter(data, cutOff, fs, order=4):
    b, a = butter_lowpass(cutOff, fs, order=order)
    y = lfilter(b, a, data)
    return y

cutOff = 23.1 #cutoff frequency in rad/s
fs = 188.495559 #sampling frequency in rad/s
order = 20 #order of filter

#print sticker_data.ps1_dxdt2

y = butter_lowpass_filter(data, cutOff, fs, order)
plt.plot(y)

Я очень смущен этим, хотя, потому что я почти уверен, что функция "butter" принимает частоту отсечки и частоту дискретизации в рад / с, но я, похоже, получаю странный вывод. Это на самом деле в Гц?

Во-вторых, какова цель этих двух строк:

    nyq = 0.5 * fs
    normalCutoff = cutOff / nyq

Я знаю что-то о нормализации, но я подумал, что nyquist был в 2 раза больше, чем выборка, а не половина. И почему вы используете Найквист в качестве нормализатора?

Можно ли объяснить больше о том, как создавать фильтры с этими функциями?

Я построил фильтр с помощью

w, h = signal.freqs(b, a)
plt.plot(w, 20 * np.log10(abs(h)))
plt.xscale('log')
plt.title('Butterworth filter frequency response')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.show()

и получил это, что явно не обрезается при 23 рад / с:

Answer 1

Несколько комментариев:

• Частота Найквиста составляет половину частоты дискретизации.
• Вы работаете с данными с регулярной выборкой, поэтому вам нужен цифровой фильтр, а не аналоговый фильтр. Это означает, что вы не должны использовать analog=True в призыве к butter, и вы должны использовать scipy.signal.freqz (не freqs) для генерации частотного отклика.
• Одна из целей этих коротких служебных функций - позволить вам оставить все ваши частоты, выраженные в Гц. Вам не нужно конвертировать в рад / сек. Пока вы выражаете свои частоты единообразными единицами, масштабирование функций утилит позаботится о нормализации для вас.

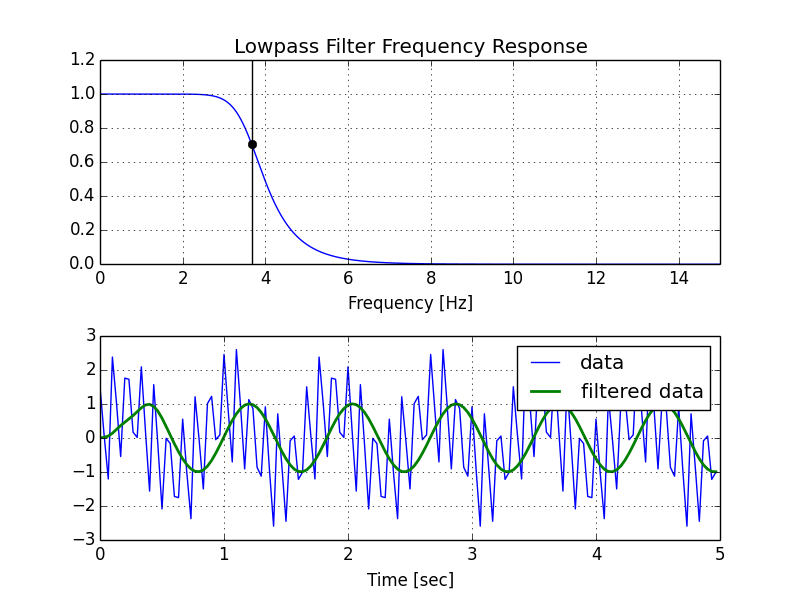
Вот моя модифицированная версия вашего скрипта, а затем сюжет, который он генерирует.

import numpy as np
from scipy.signal import butter, lfilter, freqz
import matplotlib.pyplot as plt


def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def butter_lowpass_filter(data, cutoff, fs, order=5):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y


# Filter requirements.
order = 6
fs = 30.0       # sample rate, Hz
cutoff = 3.667  # desired cutoff frequency of the filter, Hz

# Get the filter coefficients so we can check its frequency response.
b, a = butter_lowpass(cutoff, fs, order)

# Plot the frequency response.
w, h = freqz(b, a, worN=8000)
plt.subplot(2, 1, 1)
plt.plot(0.5*fs*w/np.pi, np.abs(h), 'b')
plt.plot(cutoff, 0.5*np.sqrt(2), 'ko')
plt.axvline(cutoff, color='k')
plt.xlim(0, 0.5*fs)
plt.title("Lowpass Filter Frequency Response")
plt.xlabel('Frequency [Hz]')
plt.grid()


# Demonstrate the use of the filter.
# First make some data to be filtered.
T = 5.0         # seconds
n = int(T * fs) # total number of samples
t = np.linspace(0, T, n, endpoint=False)
# "Noisy" data.  We want to recover the 1.2 Hz signal from this.
data = np.sin(1.2*2*np.pi*t) + 1.5*np.cos(9*2*np.pi*t) + 0.5*np.sin(12.0*2*np.pi*t)

# Filter the data, and plot both the original and filtered signals.
y = butter_lowpass_filter(data, cutoff, fs, order)

plt.subplot(2, 1, 2)
plt.plot(t, data, 'b-', label='data')
plt.plot(t, y, 'g-', linewidth=2, label='filtered data')
plt.xlabel('Time [sec]')
plt.grid()
plt.legend()

plt.subplots_adjust(hspace=0.35)
plt.show()