OpenCV DFT_INVERSE отличается от ifft Matlab

Question

Я пытаюсь отфильтровать сигнал, используя функцию dft opencv. То, как я пытаюсь это сделать, принимает сигнал во временной области:

x = [0.0201920000000000 -0.0514940000000000 0.0222140000000000  0.0142460000000000  -0.00313500000000000    0.00270600000000000 0.0111770000000000  0.0233470000000000  -0.00162700000000000    -0.0306280000000000 0.0239410000000000  -0.0225840000000000 0.0281410000000000  0.0265510000000000  -0.0272180000000000 0.0223850000000000  -0.0366850000000000 0.000515000000000000    0.0213440000000000  -0.0107180000000000 -0.0222150000000000 -0.0888300000000000 -0.178814000000000  -0.0279280000000000 -0.144982000000000  -0.199606000000000  -0.225617000000000  -0.188347000000000  0.00196200000000000 0.0830530000000000  0.0716730000000000  0.0723950000000000]

Преобразуйте его в домен FOURIER, используя:

cv::dft(x, x_fft, cv::DFT_COMPLEX_OUTPUT, 0);

Устранить нежелательные частоты:

for(int k=0; k<32;k++){
        if(k==0 || k>6 )
        {
            x_fft.ptr<float>(0)[2*k+0]=0;
            x_fft.ptr<float>(0)[2*k+1]=0;

        }
    }

Преобразовать его обратно во временную область:

cv::dft(x_fft, x_filt, cv::DFT_INVERSE, 0);

Чтобы проверить свои результаты, я сравнил их с Matlab. Я взял тот же сигнал х, преобразовать его в FOURIER, используя x_mfft = fft(x); Результаты аналогичны тем, которые я получаю из opencv, за исключением того, что в opencv я получаю только левую сторону, в то время как в matlab я также получаю симметричные значения. После этого я установил 0 в Matlab значения x_mfft(0) and x_mfft(8:32) и теперь сигнал выглядит точно так же, за исключением того факта, что в Matlab они находятся в сложной форме, в то время как в opencv они разделены, действительная часть в одном канале, мнимая часть в другом.

Проблема в том, что когда я выполняю обратное преобразование в Matlab, используя x_mfilt = ifft(x_mfft) результаты полностью отличаются от того, что я получаю с помощью opencv.Matlab:

0.0126024108604191 + 0.0100628178150509i    0.00278762121814893 - 0.00615997579216921i  0.0116716145588075 - 0.0150834711251450i    0.0204808089882897 - 0.00937680194210788i   0.0187164132302469 - 0.000843687942567208i  0.0132322795522116 - 0.000108642129381095i  0.0140282455278201 - 0.00325620843335947i   0.0190436542174946 - 0.000556561558544529i  0.0182379867325824 + 0.00764390022568001i   0.00964801276734883 + 0.0107158342431018i   0.00405220362962359 + 0.00339496875258604i  0.0108096973356501 - 0.00476499376334313i   0.0236507440224628 - 0.000415067678294738i  0.0266197220512826 + 0.0154626911663024i    0.0142805873081583 + 0.0267004219364679i    0.000314527358302778 + 0.0215255889620223i  0.00173512964620177 + 0.00865151513638104i  0.0169666351363477 + 0.00836162056544561i   0.0255915540012784 + 0.0277878383595920i    0.0118710562486680 + 0.0506446948330055i    -0.0160165379892836 + 0.0553846122152651i   -0.0354343989166415 + 0.0406080858067314i   -0.0370261047451452 + 0.0261077990289579i   -0.0365120038155127 + 0.0268311542287801i   -0.0541841640123775 + 0.0312446266697320i   -0.0854132555297956 + 0.0125342802025550i   -0.0989182320365535 - 0.0377079727602073i   -0.0686133217915410 - 0.0925138855355046i   -0.00474198249025186 - 0.111728716441247i   0.0515933837210975 - 0.0814138940625859i    0.0663201317560107 - 0.0279433757588921i    0.0426055814586485 + 0.00821080477569232i

OpenCV после cv::dft(x_fft, x_filt, cv::DFT_INVERSE, 0);

Канал 1:

0.322008 -0.197121 -0.482671 -0.300055 -0.026996 -0.003475 -0.104199 -0.017810 0.244606 0.342909 0.108642 -0.152477 -0.013281 0.494806 0.854412 0.688818 0.276848 0.267571 0.889207 1.620622 1.772298 1.299452 0.835450 0.858602 0.999833 0.401098 -1.206658 -2.960446 -3.575316 -2.605239 -0.894184 0.262747 

Канал 2:

0.403275 0.089205 0.373494 0.655387 0.598925 0.423432 0.448903 0.609397 0.583616 0.308737 0.129670 0.345907 0.756820 0.851827 0.456976 0.010063 0.055522 0.542928 0.818924 0.379870 -0.512527 -1.133893 -1.184826 -1.168379 -1.733893 -2.733226 -3.165383 -2.195622 -0.151738 1.650990 2.122242 1.363375 

Что мне не хватает? Разве результаты не должны быть похожими? Как я могу проверить, правильно ли выполнено обратное преобразование в opencv?

Позже РЕДАКТИРОВАТЬ: После нескольких часов борьбы с проблемами я решил представить результаты Matlab и OpenCV, и, к моему удивлению, они были очень похожи.

Мнимые части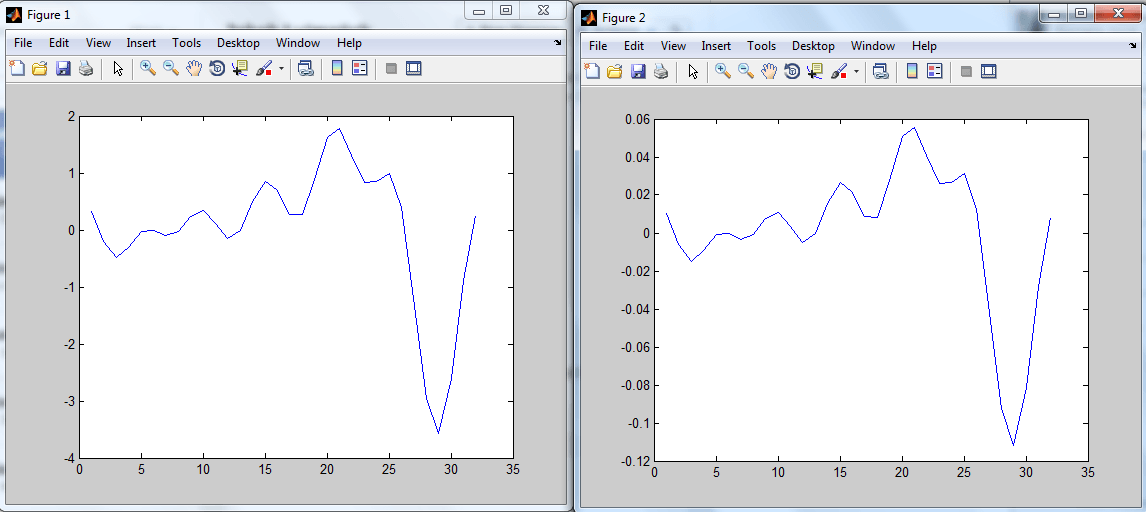

Реальные части: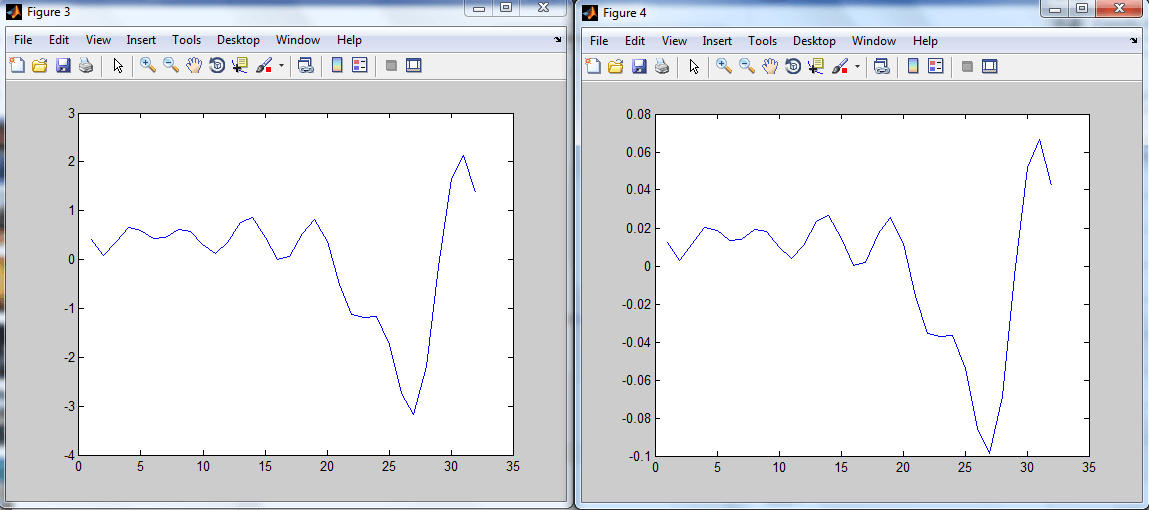

Так что, очевидно, это что-то о масштабе. После деления их по элементам, по-видимому, этот коэффициент равен 32 - длине сигнала. Может кто-нибудь объяснить, почему это происходит? Очевидное решение заключается в использовании cv::dft(x_fft, x_filt, cv::DFT_INVERSE+cv::DFT_SCALE, 0); так что я думаю, что на эту тему ответили, но я все еще интересуюсь, почему это так.

Answer 1

Не существует стандарта для масштабного коэффициента, используемого всеми библиотеками FFT. Некоторые не используют ничего, некоторые включают масштабный коэффициент 1/N, некоторые 1/sqrt(N). Вы должны проверить или посмотреть в документации для каждой конкретной библиотеки.