Как упростить сплайн?

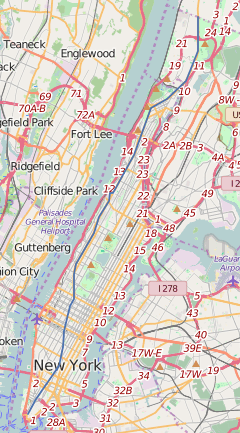
У меня есть интересная алгоритмическая задача в проекте, над которым я работаю. У меня есть отсортированный список координатных точек, указывающих на здания по обе стороны улицы, которые при достаточном увеличении выглядят так:

Я хотел бы взять этот зигзаг и сгладить его, чтобы линеаризовать основную улицу.

Я могу придумать пару решений:

  1. Рассчитайте центроиды, используя скользящие средние из шести или около того точек, и используйте их.
  2. Сплайн регрессия.

Есть ли лучший или лучший способ решения этой проблемы? (Я использую Python 3.5)

Источник

2 ответа

Решение

Пост Дали правильно предполагает, что для этой задачи полезен алгоритм упрощения строк. Перед тем как опубликовать этот вопрос, я на самом деле изучил несколько таких алгоритмов, но мне было не совсем удобно, потому что, несмотря на то, что они привели к упрощенной геометрии, которая мне понравилась, они напрямую не решали проблему, связанную с точками нахождения по обе стороны от особенность и никогда не в середине.

Таким образом я использовал двухступенчатый процесс:

  1. Я вычислил центроиды полилинии, используя скользящее среднее из координат пяти окружающих точек. Это не сильно помогло сгладить функцию, но, в основном, им удалось переназначить их на середину улицы.
  2. Я применил алгоритм Висвалингама к новой полилинии, с n=20 указанные точки (используя эту замечательную реализацию).

Результат был не совсем идеальным, но достаточно хорошим:

Спасибо всем за помощь!

Источник

Основываясь на вашем описании и ваших комментариях, вы ищете алгоритмы упрощения линии.

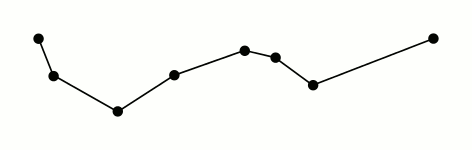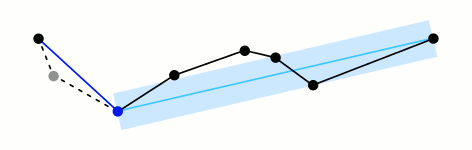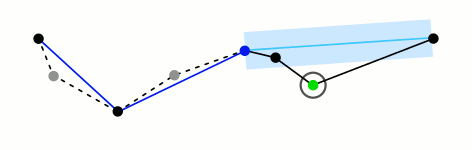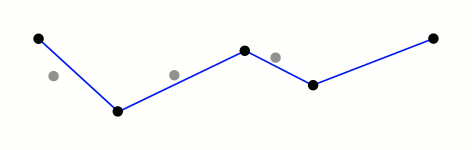
Алгоритм Рамера-Дубласа (предложенный в комментарии), скорее всего, является наиболее известным алгоритмом в этом семействе, но их гораздо больше.

Например , алгоритм Висвалингама работает, удаляя точку с наименьшим изменением, которая рассчитывается по наименьшему квадрату треугольника. Это делает его очень простым для написания кода и интуитивно понятным. Если вам трудно читать исследовательскую работу, вы можете прочитать эту простую статью.

Другие алгоритмы в этом семействе:

Прочитайте о них, поймите, что они пытаются минимизировать и выберите наиболее подходящий для вас.

Источник
Другие вопросы по тегам