Комбинации

Question

int f(int n,int a,int x)
{
        if(a==1)
        {
            if(n>=0 && n<=x)  //HERE WAS ERROR,sorry
                return 1;
            else 
                return 0;
        }

        int ans=0;

        for(int i=0;i<=x;i++)
            ans += f(n-i,a-1,x);

    return ans;
}

Здравствуйте!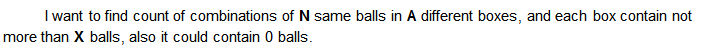

Пример:

Вот алгоритм, но он тратит очень много времени. Может быть, вы знаете более быстрый способ решения этой проблемы? Большое спасибо и извините за беспокойство.

Answer 1

Что вам нужно, это динамическое программирование. Вам нужно запомнить значения функции f для тех аргументов, для которых она уже была рассчитана. Также это может быть реализовано без рекурсии следующим образом:

int f(int n,int a,int x)
{
    int q[1000][50]; // to simplify and not use dynamic allocation assume that a < 50 and n < 1000

    q[0][0] = 1;
    for (int i = 1; i < 1000; ++i)
        q[i][0] = 0;

    for (int i = 1; i <= a; ++i)
    {
        for (int j = 0; j <= n; j++)
        {
            int t = 0;
            for (int l = 0; l <= j && l <= x; ++l)
                t += q[j - l][i-1];
            q[j][i] = t;
        }
    }

    return q[n][a];
}

Это всего лишь простая техника демонстрации. Его можно оптимизировать еще раз, вы можете предварительно рассчитать t-сумму и исключить цикл для l. И вам не нужно хранить всю таблицу q, вам нужно всего два слоя, это уменьшит использование памяти. Таким образом, результат будет выглядеть так:

int f(int n,int a,int x)
{
    int q[1000][2]; // to simplify and not use dynamic allocation assume n < 1000

    q[0][0] = 1;
    for (int i = 1; i < 1000; ++i)
        q[i][0] = 0;

    int current = 1;
    for (int i = 1; i <= a; ++i)
    {
        int t = 0;
        for (int j = 0; j <= n; j++)
        {
            t += q[j][1 - current];
            if (j > x)
                t -= q[j - x - 1][1 - current];

            q[j][current] = t;
        }
        current = 1 - current;
    }

    return q[n][1 - current];
}

Так что, наконец, потребуется O(a*n) время для вычисления.

PS: обратите внимание, что ответ может быть огромным числом, которое может переполнить любой натуральный целочисленный тип.

Answer 2

Посмотрите на http://www.mathpages.com/home/kmath337.htm и формулу внизу страницы.

Answer 3

Прежде всего, если A*X < N, нет возможности распределить шары, поэтому вы можете остановиться раньше. Если A*X == NЕсть только один способ. Тогда, вероятно, быстрее сначала выбрать количество ящиков, в которые вы помещаете X шары и повторяются с меньшим лимитом.

int f(int n, int a, int x){   // should all be unsigned, actually
    if (n == 0){
        return 1;
    }
    int p = a*x;
    if (p < n){
        return 0;
    }
    if (p == n){
        return 1;
    }
    if (x == 1){
        return binom(a,n);    // ways to choose n boxes from a boxes
    }
    // now the interesting cases
    int ways = 0;    // should perhaps be unsigned long long, that number grows fast
    int xCount, tempRes, min, max;
    min = a+n-p;
    if (min < 0) min = 0;
    max = n/x;
    for(xCount = min; xCount <= max; ++xCount){
        tempRes = f(n - x*xCount,a - xCount, x-1); // ways to distribute the remaining balls
        ways += binom(a,xCount)*tempRes;    // multiply by the number of ways to choose xCount boxes
    }
    return ways;
}

Может быть полезно создать таблицу для биномиальных коэффициентов, если вы вызываете f довольно часто.