Алгоритм Форда-Фулкерсона на графе с двусторонними ребрами
У меня возникли проблемы с пониманием алгоритма Форда-Фулкерсона для определения максимального потока, и я надеялся на некоторую помощь.
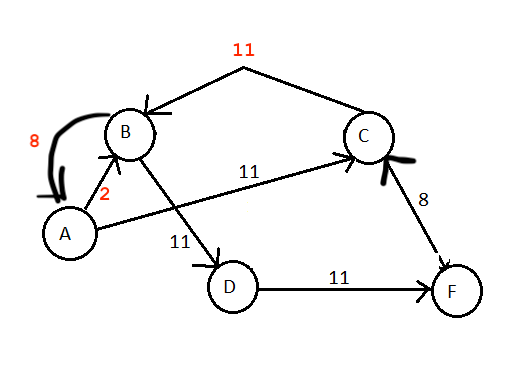
Если мы посмотрим на следующий график с источником A и стоком F, где емкости ребер указаны на каждом ребре.
Вы заметите, что узлы B и C имеют двусторонний фронт, BC имеют емкость 8, а CB - 3.
Теперь предположим, что первый путь найден - это ABCF, где емкость узкого места равна 8. Таким образом, мы создаем поток 8 на пути, создавая этот график: 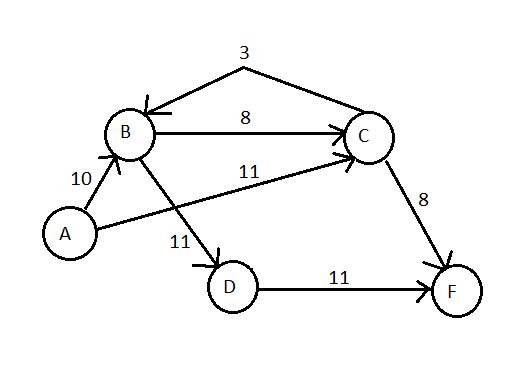
Теперь давайте скажем, что следующий путь - ACBDF.
У меня вопрос, какой поток мы теперь можем протолкнуть через CB? Это 11 с использованием 8 уже протолкнутого потока вместе с емкостью 3 на другом краю, или это только 3 или, возможно, 8?
Спасибо за ваше время.
2 ответа
Я думаю, что вы построили второй остаточный граф неправильно. Вот версия, которую я подготовил из первого графика.
Всякий раз, когда вы пропускаете поток в увеличивающуюся траекторию, вам необходимо отрегулировать пропускную способность вместе с ней. Следовательно, когда вы передали поток со значением 8 по пути ABCF, вам необходимо отрегулировать пропускную способность связанных ребер перед передачей следующего потока в график.
Следовательно, значение 8 получено из емкости узкого места края BC или CF. Поскольку вы прошли максимальный поток вдоль этих двух ребер, и вы не можете пройти больше 8, значит, вы максимально использовали пропускную способность этих ребер. Это обобщает идею о том, что всякий раз, когда вы пропускаете некоторый поток, используя некоторые ребра, вам нужно рисовать обратные ребра со значениями потока, добавленными с емкостью обратных ребер и вычтенными из передних ребер.
Вы можете видеть это из моей версии вашего второго графика. Поскольку у BC больше нет возможности переносить дополнительный поток (8 - 8 = 0), я опустил край и добавил емкость к обратному краю (то есть CB, где емкость была увеличена до 3 + 8 = 11). То же самое произошло и с МВ.
Теперь для AB, так как мы прошли 8 вместе с путем с емкостью 10, у нас еще осталось 2 емкости для прохождения большего потока. Отсюда мы вычитаем значение из AB и получаем (10 - 8 = 2). Мы также добавляем обратный край BA, который создается, добавляя значение потока (то есть 0 + 8 = 8).
Теперь, когда мы правильно построили наш остаточный граф, единственный оставшийся путь расширения, который может переносить поток от AF, - это ABDF со значением потока 2 (емкость узкого места равна 2).
Следовательно, максимальное значение потока (общее значение потока) составляет 8 + 2 = 10
Надеюсь, это поможет!
Я думаю, что решение, предоставленное Reaz, неверно. Потому что есть еще увеличивающий путь ACBDF. (или, если посмотреть на глаз, минимальное сечение 11+8), что помогает проиллюстрировать, что максимальный поток равен 19.
Теперь переходим к проблеме. Возможная «нелогичная» часть может состоять в том, что сначала мы вводим поток 8 по ABCF, но затем мы вводим в противоположном направлении по пути BC поток 8, и, используя уже существующее ребро CB (мощность 3), мы может ввести другой поток со значением 11 вдоль ACBDF и получить значение потока (максимальный поток) 19. Но, возможно, вы можете думать об этом. Мы можем разложить поток следующим образом (кстати, это всегда возможно по теореме о разложении потока).
значение расхода 8: ABDF
Обратите внимание, что после «извлечения» вышеприведенного потока на ребрах BD и DF по-прежнему остается остаточная емкость, равная 3.
значение расхода 8: ACF
где AC в настоящее время все еще имеет остаточную емкость 3.
значение расхода 3: ACBDF
Надеюсь, это поможет!