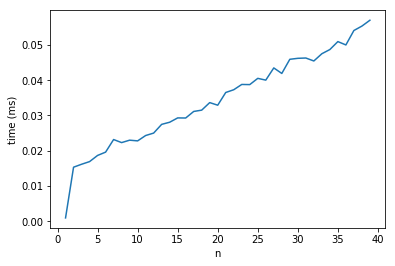
Масштабирование времени для трансляции операции над трехмерными массивами в numpy
Я пытаюсь передать простую операцию ">" над двумя 3D-массивами. Один имеет размеры (m, 1, n), другой (1, m, n). Если бы я изменил значение третьего измерения (n), я бы наивно ожидал, что скорость вычисления будет масштабироваться как n.
Однако, когда я пытаюсь измерить это явно, я нахожу, что при увеличении n от 1 до 2 увеличивается время вычисления примерно в 10 раз, после чего масштабирование является линейным.
Почему время вычисления так резко увеличивается при переходе от n=1 к n=2? Я предполагаю, что это артефакт управления памятью в numpy, но я ищу больше деталей.
Код прилагается ниже с полученным сюжетом.
import numpy as np
import time
import matplotlib.pyplot as plt
def compute_time(n):
x, y = (np.random.uniform(size=(1, 1000, n)),
np.random.uniform(size=(1000, 1, n)))
t = time.time()
x > y
return time.time() - t
a = [
[
n, np.asarray([compute_time(n)
for _ in range(100)]).mean()
]
for n in range(1, 30, 1)
]
a = np.asarray(a)
plt.plot(a[:, 0], a[:, 1])
plt.xlabel('n')
plt.ylabel('time(ms)')
plt.show()
Сюжет времени для трансляции операции
2 ответа
@ Теория Павла совершенно верна. В этом ответе я использую perf и отладчик, чтобы погрузиться, чтобы поддержать эту теорию.
Во-первых, давайте посмотрим, где тратится время выполнения (точный код приведен в листингах run.py ниже).
За n=1 мы видим следующее:
Event count (approx.): 3388750000
Overhead Command Shared Object Symbol
34,04% python umath.cpython-36m-x86_64-linux-gnu.so [.] DOUBLE_less
32,71% python multiarray.cpython-36m-x86_64-linux-gnu.so [.] _aligned_strided_to_contig_size8_srcstride0
28,16% python libc-2.23.so [.] __memmove_ssse3_back
1,46% python multiarray.cpython-36m-x86_64-linux-gnu.so [.] PyArray_TransferNDimToStrided
по сравнению с n=2:
Event count (approx.): 28954250000
Overhead Command Shared Object Symbol
40,85% python libc-2.23.so [.] __memmove_ssse3_back
40,16% python multiarray.cpython-36m-x86_64-linux-gnu.so [.] PyArray_TransferNDimToStrided
8,61% python umath.cpython-36m-x86_64-linux-gnu.so [.] DOUBLE_less
8,41% python multiarray.cpython-36m-x86_64-linux-gnu.so [.] _contig_to_contig
При n=2 подсчитывается в 8,5 раз больше событий, но только для удвоенных данных, поэтому нам нужно объяснить коэффициент замедления 4.
Еще одно важное наблюдение: во время выполнения преобладают операции с памятью для n=2 и (менее очевидно) также для n=1 (_aligned_strided_to_contig_size8_srcstride0 это все о копировании данных), они перевешивают затраты для сравнения - DOUBLE_less,
Очевидно, что PyArray_TransferNDimtoStrided называется для обоих размеров, так почему же такая большая разница в его доле времени работы?
Показанное время PyArray_TransferNDimtoStrided не время, необходимое для копирования, а накладные расходы: указатели отрегулированы так, чтобы в последнем измерении можно было скопировать за один проход через stransfer:
PyArray_TransferNDimToStrided(npy_intp ndim,
....
/* A loop for dimensions 0 and 1 */
for (i = 0; i < shape1; ++i) {
if (shape0 >= count) {
stransfer(dst, dst_stride, src, src_stride0,
count, src_itemsize, data);
return 0;
}
else {
stransfer(dst, dst_stride, src, src_stride0,
shape0, src_itemsize, data);
}
count -= shape0;
src += src_stride1;
dst += shape0*dst_stride;
}
...
Эти функции переноса _aligned_strided_to_contig_size8_srcstride0 (см. сгенерированный код в списке ниже) и _contig_to_contig:
_contig_to_contigиспользуется в случаеn=2и переносы 2-х двойных (последнее измерение имеет 2 значения), накладные расходы на настройку указателей довольно высоки!_aligned_strided_to_contig_size8_srcstride0используется дляn=1и передает 1000 удвоений за вызов (как указал @Paul и, как мы скоро увидим, numpy достаточно умен, чтобы отбросить измерения, длина которых составляет 1 элемент), издержками на настройку указателей можно пренебречь.
Кстати, эти функции используются вместо простого цикла for для использования векторизации современных процессоров: с шагом, известным во время компиляции, компилятор может векторизовать код (что компиляторы часто не могут сделать для шагов, известных только в runtime), поэтому numpy анализирует схему доступа и отправляет различные предварительно скомпилированные функции.
Остался один вопрос: действительно ли numpy отбрасывает последнее измерение, если его размер равен 1, как показывают наши наблюдения?
Это легко проверить с помощью debbuger:
- данные доступа к ufunc через итератор, который создается в
iterator_loopс помощьюNpyIter_AdvancedNew - в
NpyIter_AdvancedNew, размеры анализируются (и переинтерпретируются), когдаnpyiter_coalesce_axes
Что касается фактора скорости 4 который "потерян" при сравнении n=2 в n=1: Это не имеет особого значения и является случайным значением на моей машине: изменение размера матрицы с 10^3 до 10^4 сместит преимущество еще больше (меньше накладных расходов) еще дальше n=1 случай, который приводит на моей машине к коэффициенту потери скорости 12.
run.py
import sys
import numpy as np
n=int(sys.argv[1])
x, y = (np.random.uniform(size=(1, 1000, n)),
np.random.uniform(size=(1000, 1, n)))
for _ in range(10000):
y<x
а потом:
perf record python run.py 1
perf report
....
perf record python run.py 2
perf report
Сгенерированный источник _aligned_strided_to_contig_size8_srcstride0:
/*
* specialized copy and swap for source stride 0,
* interestingly unrolling here is like above is only marginally profitable for
* small types and detrimental for >= 8byte moves on x86
* but it profits from vectorization enabled with -O3
*/
#if (0 == 0) && 1
static NPY_GCC_OPT_3 void
_aligned_strided_to_contig_size8_srcstride0(char *dst,
npy_intp dst_stride,
char *src, npy_intp NPY_UNUSED(src_stride),
npy_intp N, npy_intp NPY_UNUSED(src_itemsize),
NpyAuxData *NPY_UNUSED(data))
{
#if 8 != 16
# if !(8 == 1 && 1)
npy_uint64 temp;
# endif
#else
npy_uint64 temp0, temp1;
#endif
if (N == 0) {
return;
}
#if 1 && 8 != 16
/* sanity check */
assert(npy_is_aligned(dst, _ALIGN(npy_uint64)));
assert(npy_is_aligned(src, _ALIGN(npy_uint64)));
#endif
#if 8 == 1 && 1
memset(dst, *src, N);
#else
# if 8 != 16
temp = _NPY_NOP8(*((npy_uint64 *)src));
# else
# if 0 == 0
temp0 = (*((npy_uint64 *)src));
temp1 = (*((npy_uint64 *)src + 1));
# elif 0 == 1
temp0 = _NPY_SWAP8(*((npy_uint64 *)src + 1));
temp1 = _NPY_SWAP8(*((npy_uint64 *)src));
# elif 0 == 2
temp0 = _NPY_SWAP8(*((npy_uint64 *)src));
temp1 = _NPY_SWAP8(*((npy_uint64 *)src + 1));
# endif
# endif
while (N > 0) {
# if 8 != 16
*((npy_uint64 *)dst) = temp;
# else
*((npy_uint64 *)dst) = temp0;
*((npy_uint64 *)dst + 1) = temp1;
# endif
# if 1
dst += 8;
# else
dst += dst_stride;
# endif
--N;
}
#endif/* @elsize == 1 && 1 -- else */
}
#endif/* (0 == 0) && 1 */
Я не могу доказать это, но я почти уверен, что это связано с одной простой оптимизацией, которая доступна только при n==1.
В настоящее время реализация numpy ufunc основана на сгенерированном компьютером коде для самого внутреннего цикла, который отображается на простой цикл C. Закрывающие циклы требуют использования полноценного объекта итератора, который в зависимости от полезной нагрузки, то есть размера самого внутреннего цикла и стоимости атомарной операции, может быть значительным дополнительным расходом.
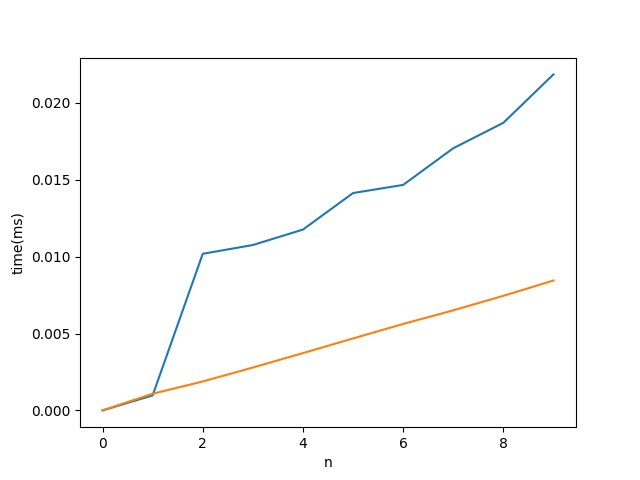
Теперь, при n == 1, проблема по существу двумерная (numpy достаточно умен, чтобы обнаружить это), с самым внутренним циклом размером 1000, следовательно, 1000 шагов объекта итератора. От n==2 и выше самый внутренний цикл имеет размер n, и у нас есть 1 000 000 шагов объекта итератора, который учитывает скачок, который вы наблюдаете.
Как я уже сказал, я не могу доказать это, но я могу сделать так, чтобы это выглядело правдоподобно: если мы переместим размер переменной вперед, то самый внутренний цикл будет иметь постоянный размер 1000, а внешний цикл будет линейно расти за 1000 шагов итерации. И действительно, это заставляет прыжок уйти.
Код:
import numpy as np
import time
import matplotlib.pyplot as plt
def compute_time(n, axis=2):
xs, ys = [1, 10], [10, 1]
xs.insert(axis, n)
ys.insert(axis, n)
x, y = (np.random.uniform(size=xs),
np.random.uniform(size=ys))
t = time.perf_counter()
x > y
return time.perf_counter() - t
a = [
[
n,
np.asarray([compute_time(n) for _ in range(100)]).mean(),
np.asarray([compute_time(n, 0) for _ in range(100)]).mean()
]
for n in range(0, 10, 1)
]
a = np.asarray(a)
plt.plot(a[:, 0], a[:, 1:])
plt.xlabel('n')
plt.ylabel('time(ms)')
plt.show()