Как создать линию произвольной толщины, используя Брезенхем?
В настоящее время я использую алгоритм Брезенхэма для рисования линий, но они (конечно) имеют толщину в один пиксель. У меня вопрос, какой самый эффективный способ рисовать линии произвольной толщины?
Я использую язык C.
10 ответов
Я думаю, что лучший способ - нарисовать прямоугольник, а не линию, поскольку линия с шириной - это двухмерный объект. Попытка нарисовать набор параллельных линий, чтобы избежать перерисовки (чтобы уменьшить пропускную способность записи) и перерисовки (отсутствующие пиксели), была бы довольно сложной. Нетрудно вычислить угловые точки прямоугольника из начальной и конечной точек и ширины.
Итак, следуя комментарию ниже, процесс для этого будет:
- Создайте прямоугольник той же длины, что и требуемая линия, и ширины, равной требуемой ширине, чтобы (от 0,0) до (ширина, длина)
- Поверните и переведите координаты углов прямоугольников в нужное положение, используя 2D-преобразование
- Растрируйте повернутый прямоугольник, используя аппаратное ускорение рендеринга (например, квадроцикл OpenGL *) или программный растеризатор. Он может быть визуализирован с использованием четырехугольного растеризатора или пары треугольников (например, вверху слева и внизу справа).
Примечание *: Если вы используете OpenGL, вы также можете выполнить Шаг 2 одновременно. Конечно, использование OpenGL означает понимание OpenGL (большого и сложного), и это приложение может сделать это сложной задачей для реализации на столь позднем этапе разработки.
Возьмите другую петлю Брезенхэма и используйте ее, чтобы изменить начальное и конечное положение исходной линии в прямоугольном направлении. Проблема состоит в том, чтобы эффективно найти правильную начальную точку и не рисовать ни один пиксель дважды (или пропустить пиксель) при рисовании следующей линии.
Рабочий и протестированный C-код доступен в Github C-коде.
Вот тестовая страница с несколькими примерами строк, созданных этим кодом. Черные пиксели являются отправной точкой для алгоритма.
Вот статья и реализация Delphi модифицированной версии алгоритма Брезенхема для рисования утолщенных линий.
Вы также можете взглянуть на Anti-Grain Geometry, библиотеку для высококачественного и высокопроизводительного программного рендеринга 2D-графики. Взгляните на демонстрационную страницу, чтобы понять, на что она способна.
Для лучшей точности, а также хорошей производительности для более толстых линий, вы можете нарисовать линию в виде многоугольника. Некоторый псевдокод:
draw_line(x1,y1,x2,y2,thickness)
Point p[4];
angle = atan2(y2-y1,x2-x1);
p[0].x = x1 + thickness*cos(angle+PI/2);
p[0].y = y1 + thickness*sin(angle+PI/2);
p[1].x = x1 + thickness*cos(angle-PI/2);
p[1].y = y1 + thickness*sin(angle-PI/2);
p[2].x = x2 + thickness*cos(angle-PI/2);
p[2].y = y2 + thickness*sin(angle-PI/2);
p[3].x = x2 + thickness*cos(angle+PI/2);
p[3].y = y2 + thickness*sin(angle+PI/2);
draw_polygon(p,4)
И, возможно, круг может быть нарисован в каждой конечной точке.
Самый простой способ создать линию практически произвольной толщины - это сначала выполнить брезенхем, а затем применить столько итераций расширения, сколько пожелаете. Каждая расширительная прокладка с обеих сторон вашей линии одинаково, но, используя разные маски, вы можете добиться как равномерной, так и неравномерной толщины:
Толщина 1:
Маска:
1 1 1
1 1 1
1 1 1
Результирующая толщина: 3
Маска:
0 1 0
1 1 1
0 1 0
Результирующая толщина: 2
Несколько простых маршрутов для использования:
- для любой ширины n, где n нечетно. для любой построенной точки p также нарисуйте точки выше / ниже ее для n/2 (если линия имеет угол> 45 градусов, то рисуйте из стороны в сторону).
- не совсем правильная линия правильной толщины, скорее как курсив, но очень быстрая.
- для начальной точки p(x,y) выберите точки t0 и b так, чтобы они центрировались на p, но на расстоянии n пикселей. для конечной точки сделайте то же самое, что приведет к t1 b1. Нарисуйте линии от t0 -> t1, t1->b1, b1 -> t0, b0 -> t1. Заполните полученный прямоугольник.
- Хитрость здесь в том, чтобы выбрать точки так, чтобы они казались ортогональными к направлению пути.
- для каждой точки p на линии вместо рисования точки нарисуйте круг.
- Это дает преимущество в том, что конечные точки становятся "чистыми" независимо от ориентации.
- не должно быть необходимости делать какие-либо круги сплошными, кроме первых.
- немного медленно
http://members.chello.at/~easyfilter/bresenham.html
Пример внизу этой ссылки - javascript, но он должен быть достаточно простым для адаптации к C. Это довольно простой алгоритм сглаживания для рисования линий переменной толщины.
Я предполагаю, что вы бы нарисовали горизонтальные отрезки от одной ограничительной линии к другой и вычислили бы значение x каждой из линий по методу Брезенхэма (по ходу цикла).
Не пробовал это.
Конечные точки могут нуждаться в некотором внимании, чтобы они не выглядели странно обрезанными.
Для тех, кто хочет версию Python, здесь приведен код (на основе ответа @Fabel):
def drawline(x1,y1,x2,y2,**kwargs):
if kwargs.get('thickness')==None:
thickness=1
else:
thickness=kwargs['thickness']
if kwargs.get('roundcap')==None:
roundcap=False
else:
roundcap=True
angle = np.arctan2(y2-y1,x2-x1)
xx = np.zeros(4)
yy = np.zeros(4)
xx[0] = np.round(x1 + thickness*np.cos(angle+np.pi/2))
yy[0] = np.round(y1 + thickness*np.sin(angle+np.pi/2))
xx[1] = np.round(x1 + thickness*np.cos(angle-np.pi/2))
yy[1] = np.round(y1 + thickness*np.sin(angle-np.pi/2))
xx[2] = np.round(x2 + thickness*np.cos(angle-np.pi/2))
yy[2] = np.round(y2 + thickness*np.sin(angle-np.pi/2))
xx[3] = np.round(x2 + thickness*np.cos(angle+np.pi/2))
yy[3] = np.round(y2 + thickness*np.sin(angle+np.pi/2))
u,v=polygon(xx,yy)
if roundcap:
temp1x, temp1y = circle(x1,y1,thickness)
temp2x, temp2y = circle(x1,y1,thickness)
u = np.append(u,temp1x,temp2x)
v = np.append(v,temp1y,temp2y)
return u,v
При вызове функции вы можете при желании указать толщину и круглую крышку. Например:
drawline(10,10,50,50,thickness=3,roundcap=False)
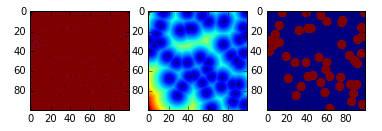
Я делаю это довольно часто, чтобы генерировать изображения волокон и сфер для моделирования пористых сред. У меня есть хороший простой способ сделать это, используя очень стандартную технику анализа изображений, известную как "преобразование расстояния". Это требует наличия доступа к некоторому пакету анализа изображений. Я использую Python со Scipy, так что это не проблема. Вот демонстрационная программа для преобразования случайно распределенных точек в сферы:
import scipy as sp
import scipy.ndimage as spim
im1 = sp.rand(100, 100) < 0.995 # Create random points in space
dt = spim.distance_transform_edt(im1)
im2 = dt < 5 # To create sphere with a radius of 5
И это все! Преобразование расстояния может быть медленным для очень больших изображений, но есть эффективная версия. Например, ImageJ имеет распараллеленный. Очевидно, что для создания толстых волокон вы просто создаете свое изображение из тонких, затем примените шаги 2 и 3 выше.
Для моего встроенного термопринтера, использующего алгоритм Брезенхэма, линия была слишком тонкой. У меня нет GL или чего-то необычного. В итоге я просто уменьшил значение Y и нарисовал больше линий под первым. Каждое число толщины добавил еще одну строку. Очень быстро внедряется и производится для получения желаемых результатов печать от монохромного растрового изображения до термического.