Что такое ссылочная прозрачность?

Question

Что означает термин ссылочная прозрачность? Я слышал, что это описывается как "это означает, что вы можете заменить равные равными", но это выглядит как неадекватное объяснение.

Answer 1

Термин "ссылочная прозрачность" происходит от аналитической философии, отрасли философии, которая анализирует конструкции, утверждения и аргументы естественного языка, основанные на методах логики и математики. Другими словами, это самая близкая тема вне компьютерной науки к тому, что мы называем семантикой языка программирования. Философ Уиллард Куайн был ответственен за инициирование концепции ссылочной прозрачности, но это также подразумевалось в подходах Бертрана Рассела и Альфреда Уайтхеда.

По своей сути "ссылочная прозрачность" - очень простая и понятная идея. Термин "референт" используется в аналитической философии, чтобы говорить о том, на что ссылается выражение. Это примерно то же самое, что мы подразумеваем под "значением" или "обозначением" в семантике языка программирования. Используя пример Эндрю Биркетта ( сообщение в блоге), термин "столица Шотландии" относится к городу Эдинбургу. Это простой пример "референта".

Контекст в предложении является "ссылочно-прозрачным", если замена термина в этом контексте другим термином, относящимся к той же сущности, не меняет смысла. Например

Шотландский парламент собирается в столице Шотландии.

означает так же, как

Парламент Шотландии встречается в Эдинбурге.

Таким образом, контекст "Шотландский парламент встречается в..." является референтно прозрачным контекстом. Мы можем заменить "столицу Шотландии" на "Эдинбург", не меняя смысла. Иными словами, контекст заботится только о том, к чему относится этот термин, и ничего более. В этом смысле контекст "ссылочно прозрачен".

С другой стороны, в предложении

Эдинбург был столицей Шотландии с 1999 года.

мы не можем сделать такую ​​замену. Если бы мы это сделали, мы бы получили "Эдинбург был Эдинбургом с 1999 года", что является сумасшедшей вещью и не имеет того же значения, что и первоначальное предложение. Таким образом, может показаться, что контекст "Эдинбург был... с 1999 года" является непрозрачным в отношении ссылок (противоположность прозрачному в отношении ссылок). По-видимому, он заботится о чем-то большем, чем то, к чему относится этот термин. Что это?

Такие вещи, как "столица Шотландии", называются определенными терминами, и в течение долгого времени они не причиняли головной боли логикам и философам. Рассел и Куайн разобрались с ними, сказав, что они на самом деле не являются "ссылочными", то есть ошибочно думать, что приведенные выше примеры используются для обозначения сущностей. Правильный способ понять, что "Эдинбург был столицей Шотландии с 1999 года", это сказать

Столица Шотландии существует с 1999 года, и эта столица - Эдинбург.

Это предложение не может быть преобразовано в сумасшедшее. Задача решена! Смысл Куайна состоял в том, чтобы сказать, что естественный язык является грязным или, по крайней мере, сложным, потому что он сделан удобным для практического использования, но философы и логики должны вносить ясность, правильно понимая их. Ссылочная прозрачность - это инструмент, который используется для придания такой ясности значения.

Какое отношение все это имеет к программированию? Не очень, на самом деле. Как мы уже говорили, ссылочная прозрачность - это инструмент, который используется для понимания языка, т. Е. При назначении значения. Кристофер Стрейчи, который основал семантику языка программирования, использовал его в своем исследовании значения. Его основополагающая статья " Основные понятия в языках программирования" доступна в Интернете. Это красивая бумага, и каждый может ее прочитать и понять. Поэтому, пожалуйста, сделайте это. Вы будете очень просветленным. Он вводит термин "ссылочная прозрачность" в этом параграфе:

Одним из наиболее полезных свойств выражений является то, что Куайн называет ссылочной прозрачностью. По сути это означает, что если мы хотим найти значение выражения, которое содержит подвыражение, единственное, что нам нужно знать о подвыражении, это его значение. Любые другие особенности подвыражения, такие как его внутренняя структура, количество и характер его компонентов, порядок, в котором они оцениваются, или цвет чернил, в которых они написаны, не имеют отношения к значению основного выражение.

Использование "по существу" предполагает, что Стрейчи перефразирует его, чтобы объяснить его простыми словами. Функциональные программисты, кажется, понимают этот абзац по-своему. Есть 9 других случаев "ссылочной прозрачности" в статье, но они, кажется, не беспокоятся ни о каких других. Фактически вся статья Стрейчи посвящена объяснению значения императивных языков программирования. Но сегодня функциональные программисты утверждают, что императивные языки программирования не являются ссылочно прозрачными. Стрейчи будет превращаться в его могилу.

Мы можем спасти ситуацию. Мы сказали, что естественный язык "грязный или, по крайней мере, сложный", потому что он сделан удобным для практического использования. Языки программирования одинаковы. Они "грязные или, по крайней мере, сложные", потому что они сделаны так, чтобы они были удобны для практического использования. Это не значит, что они должны нас смущать. Они просто должны быть поняты правильно, используя мета-язык, который является ссылочно прозрачным, чтобы у нас была ясность смысла. В статье, которую я цитировал, Стрейчи делает именно это. Он объясняет значение императивных языков программирования, разбивая их на элементарные понятия, нигде не теряя ясности. Важной частью его анализа является указание на то, что выражения в языках программирования имеют два вида "значений", называемых l-значениями и r-значениями. До статьи Стрейчи это не было понято, и воцарилась путаница. Сегодня определение C упоминает об этом регулярно, и каждый программист C понимает это различие. (Понимают ли программисты на других языках это одинаково хорошо, трудно сказать.)

И Куайн, и Стрейчи были обеспокоены значением языковых конструкций, которые включают некоторую форму зависимости от контекста. Например, наш пример "Эдинбург является столицей Шотландии с 1999 года" означает тот факт, что "столица Шотландии" зависит от времени, в которое она рассматривается. Такая зависимость от контекста является реальностью, как на естественных языках, так и на языках программирования. Даже в функциональном программировании свободные и связанные переменные должны интерпретироваться с учетом контекста, в котором они появляются. Зависимость от контекста любого вида так или иначе блокирует ссылочную прозрачность. Если вы попытаетесь понять значение терминов без учета контекста, от которого они зависят, вы снова получите путаницу. Куайна интересовало значение модальной логики. Он считал, что модальная логика была непрозрачной по ссылкам, и ее следует очистить, переведя ее в референтно прозрачную структуру (например, рассматривая необходимость как доказуемость). Он в значительной степени проиграл эту дискуссию. Логики и философы одинаково сочли возможную мировую семантику Крипке совершенно адекватной. Подобная ситуация также царит с императивным программированием. Зависимость от состояния, объясненная Стрейчи, и зависимость от магазина, объясненная Рейнольдсом (аналогично возможной мировой семантике Крипке) вполне адекватны. Функциональные программисты не знают многого из этого исследования. Их идеи относительно ссылочной прозрачности следует воспринимать с большой долей соли.

[Дополнительное примечание: Приведенные выше примеры показывают, что простая фраза, такая как "столица Шотландии", имеет несколько уровней значения. На одном уровне мы можем говорить о столице в настоящее время. На другом уровне мы могли бы говорить о всех возможных столицах, которые Шотландия могла иметь с течением времени. Мы можем "увеличить" конкретный контекст и "уменьшить", чтобы довольно легко охватить все контексты в обычной практике. Эффективность естественного языка использует нашу способность сделать это. Императивные языки программирования эффективны практически так же. Мы можем использовать переменную x в правой части присваивания (значение r), чтобы говорить о ее значении в определенном состоянии. Или мы можем говорить о его l-значении, которое охватывает все состояния. Людей редко смущают такие вещи. Однако они могут или не могут точно объяснить все слои значения, присущие языковым конструкциям. Все такие слои значения не обязательно являются "очевидными", и это вопрос науки, чтобы изучить их должным образом. Однако неспособность простых людей объяснять такие многоуровневые значения не означает, что они смущены ими.]

Отдельный "постскриптум" ниже связывает это обсуждение с проблемами функционального и императивного программирования.

Answer 2

Ссылочная прозрачность, термин, обычно используемый в функциональном программировании, означает, что при наличии функции и входного значения вы всегда будете получать один и тот же результат. То есть в функции не используется внешнее состояние.

Вот пример ссылочной прозрачной функции:

int plusOne(int x)
{
  return x+1;
}

С помощью ссылочной прозрачной функции, с учетом входных данных и функции, вы можете заменить ее значением вместо вызова функции. Таким образом, вместо вызова plusOne с параметром 5, мы могли бы просто заменить его на 6.

Еще один хороший пример - математика в целом. В математике с заданной функцией и входным значением она всегда будет отображаться на одно и то же выходное значение. f(x) = x + 1. Поэтому функции в математике являются ссылочно прозрачными.

Эта концепция важна для исследователей, потому что она означает, что когда у вас есть ссылочно-прозрачная функция, она легко поддается автоматическому распараллеливанию и кешированию.

Ссылочная прозрачность всегда используется в функциональных языках, таких как Haskell.

-

В отличие от этого существует понятие ссылочной непрозрачности. Это означает обратное. Вызов функции может не всегда давать один и тот же вывод.

//global G
int G = 10;

int plusG(int x)
{//G can be modified externally returning different values.
  return x + G;
}

Другой пример - функция-член на объектно-ориентированном языке программирования. Функции-члены обычно работают с переменными-членами и, следовательно, будут непрозрачными для ссылок. Функции-члены могут, конечно, быть прозрачными по ссылкам.

Еще один пример - функция, которая читает текстовый файл и печатает вывод. Этот внешний текстовый файл может измениться в любое время, поэтому функция будет непрозрачной.

Answer 3

Ссылочно-прозрачная функция - это функция, которая зависит только от ее ввода.

Answer 4

[Это постскриптум к моему ответу от 25 марта, чтобы приблизить обсуждение к проблемам функционального / императивного программирования.]

Представление функциональных программистов о ссылочной прозрачности, кажется, отличается от стандартного понятия тремя способами:

• В то время как философы / логики используют такие термины, как "ссылка", "обозначение", "designatum" и "bedeutung" (немецкий термин Фреге), функциональные программисты используют термин "значение". (Это не совсем их работа. Я замечаю, что Лэндин, Стрейчи и их потомки также использовали термин "ценность", чтобы говорить об упоминании / обозначении. Это может быть просто терминологическое упрощение, которое представили Ландин и Стрейчи, но, похоже, оно делает большая разница при использовании наивно.)

• Функциональные программисты, похоже, считают, что эти "ценности" существуют внутри языка программирования, а не снаружи. При этом они отличаются как от философов, так и от семантиков языка программирования.

• Кажется, они считают, что эти "ценности" должны быть получены путем оценки.

Например, в статье в Википедии о прозрачности ссылок сегодня утром говорится:

Выражение называется прозрачным по ссылкам, если его можно заменить значением, не изменяя поведение программы (другими словами, получая программу с такими же эффектами и выходными данными на одном входе).

Это полностью противоречит тому, что говорят философы / логики. Они говорят, что контекст является ссылочным или прозрачным по ссылкам, если выражение в этом контексте может быть заменено другим выражением, которое ссылается на то же самое (выражение coreferential). Кто эти философы / логики? Среди них Фреге, Рассел, Уайтхед, Карнап, Куайн, Черч и многие другие. Каждый из них - высокая фигура. Объединенная интеллектуальная сила этих логиков потрясающая, если не сказать больше. Все они единодушны в том положении, что ссылки / обозначения существуют вне формального языка, и выражения в языке могут говорить только о них. Таким образом, все, что можно сделать в языке, - это заменить одно выражение другим выражением, относящимся к той же сущности. Сами ссылки / обозначения не существуют внутри языка. Почему функциональные программисты отклоняются от этой устоявшейся традиции?

Можно предположить, что семантики языка программирования могли ввести их в заблуждение. Но они этого не сделали.

Landin:

(a) каждое выражение имеет вложенную структуру подвыражения, (b) каждое подвыражение обозначает что-то (обычно число, значение истинности или числовую функцию), (c) то, что обозначает выражение, т. е. его "значение", зависит только от значения его подвыражений, а не о других их свойствах. [Добавлен акцент]

Стой:

Единственное, что имеет значение в выражении, - это его значение, и любое подвыражение может быть заменено любым другим равным по значению значением [Добавлено выделение]. Более того, значение выражения в определенных пределах одинаково, когда бы оно ни происходило ".

Птица и Вадлер:

значение выражения зависит только от значений составляющих его выражений (если они есть), и эти подвыражения могут быть свободно заменены другими, имеющими такое же значение [Добавлено выделение].

Таким образом, в ретроспективе, попытки Ландина и Стрейчи упростить терминологию путем замены "ссылки"/"обозначения" на "значение" могли быть неразумными. Как только кто-то слышит о "ценности", возникает соблазн думать о процессе оценки, который ведет к нему. Не менее заманчиво думать о том, что оценка производит, как о "ценности", хотя может быть совершенно ясно, что это не означает. Это то, что я понимаю, что случилось с понятием "ссылочной прозрачности" в глазах функциональных программистов. Но "ценность", о которой говорили ранние семантики, не является результатом оценки или результата функции или любой другой вещи. Это обозначение термина.

Как только мы понимаем так называемую "ценность" выражения ("ссылка" или "обозначение" в дискурсе классических философов) как сложный математический / концептуальный объект, открываются все виды возможностей.

• Стрейчи интерпретировал переменные в императивных языках программирования как L-значения, как упоминалось в моем ответе от 25 марта, который представляет собой сложный концептуальный объект, который не имеет прямого представления в синтаксисе языка программирования.
• Он также интерпретировал команды на таких языках как функции от состояния к состоянию, еще один пример сложного математического объекта, который не является "значением" в синтаксисе.
• Даже вызов функции с побочным эффектом в C имеет четко определенное "значение" в качестве преобразователя состояний, который отображает состояния в пары состояний и значений (так называемая "монада" в терминологии функциональных программистов).

Нежелание функциональных программистов называть такие языки "ссылочно-прозрачными" просто подразумевает, что они не хотят признавать такие сложные математические / концептуальные объекты как "ценности". С другой стороны, они, похоже, совершенно готовы назвать преобразователь состояния "значением", когда он помещен в их собственный любимый синтаксис и дополнен модным словом "монада". Я должен сказать, что они совершенно непоследовательны, даже если мы дадим им понять, что их идея "ссылочной прозрачности" имеет некоторую согласованность.

Немного истории может пролить свет на то, как возникли эти заблуждения. Период между 1962 и 1967 годами был очень интенсивным для Кристофера Стрейчи. В период с 1962 по 1965 год он работал неполный рабочий день в качестве помощника исследователя в Морисе Уилксе для разработки и реализации языка программирования, получившего название CPL. Это был императивный язык программирования, но он должен был также иметь мощные функциональные возможности языка программирования. Ландин, который был сотрудником Strachey в своей консалтинговой компании, оказал огромное влияние на взгляды Strachey на языки программирования. В знаковой статье 1965 года " Следующие 700 языков программирования" Ландин безоговорочно продвигает функциональные языки программирования (называя их денотативными языками) и описывает императивные языки программирования как их "антитезу". В последующем обсуждении мы видим, что Стрейчи вызывает сомнения в сильной позиции Лэндина.

... DL образуют подмножество всех языков. Это интересное подмножество, но его неудобно использовать, если вы к нему не привыкли. Мы нуждаемся в них, потому что в настоящее время мы не знаем, как построить доказательства с языками, которые включают императивы и скачки. [Добавлен акцент]

В 1965 году Стрейчи занял должность читателя в Оксфорде и, по-видимому, работал практически полный рабочий день над разработкой теории императивов и прыжков. К 1967 году он был готов с теорией, которую он преподавал в своем курсе " Фундаментальные концепции в языках программирования" в летней школе в Копенгагене. Предполагалось, что конспекты лекций были опубликованы, но "к сожалению, из-за расточительного редактирования материалы так и не были реализованы; как и большая часть работы Стрэчи в Оксфорде, однако, газета имела влиятельный частный тираж". ( Мартин Кэмпбелл-Келли)

Трудность получения работ Стрейчи могла привести к распространению путаницы, когда люди полагались на вторичные источники и слухи. Но теперь, когда " Фундаментальные концепции" легко доступны в Интернете, нет необходимости прибегать к угадыванию работы. Мы должны прочитать это и решить, что имел в виду Стрейчи. Особенно:

• В разделе 3.2 он имеет дело с "выражениями", где он говорит о "ссылочной прозрачности R-значения".
• Его раздел 3.3 посвящен "командам", где он говорит о "ссылочной прозрачности L-значения".
• В разделе 3.4.5 он говорит о "функциях и процедурах" и заявляет, что "любое отклонение ссылочной прозрачности R-значения в контексте R-значения должно быть либо устранено путем разложения выражения на несколько команд и более простых выражений, либо, если это оказывается трудным, предметом комментария."

Любой разговор о "ссылочной прозрачности" без понимания различия между L-значениями, R-значениями и другими сложными объектами, которые населяют концептуальную вселенную императивного программиста, в корне ошибочен.

Answer 5

Выражение является ссылочно прозрачным, если его можно заменить его значением, не изменяя алгоритм, что приводит к алгоритму, который имеет те же эффекты и выводит на тот же вход.

Answer 6

Ссылочно-прозрачная функция - это функция, которая действует как математическая функция; при одинаковых входах он всегда будет давать одинаковые выходы. Это означает, что переданное состояние не изменяется, и что функция не имеет собственного состояния.

Answer 7

Для тех, кто нуждается в кратком объяснении, я рискну (но прочитайте раскрытие ниже).

Ссылочная прозрачность в языке программирования способствует рациональному рассуждению - чем больше у вас ссылочной прозрачности, тем легче проводить эквациональное рассуждение. Например, с (псевдо) определением функции,

fx = x + x,

Простота, с которой вы можете (безопасно) заменить f (foo) на foo + foo в рамках этого определения, не имея слишком много ограничений на то, где вы можете выполнить это сокращение, является хорошим показателем того, насколько ссылочная прозрачность вашего языка программирования есть.

Например, если бы foo был x++ в смысле программирования на C, то вы не могли бы безопасно выполнить это сокращение (то есть, если бы вы выполняли это сокращение, вы не получили бы ту же самую программу, с которой начали).

В практических языках программирования вы не увидите идеальной ссылочной прозрачности, но функциональные программисты заботятся об этом больше, чем о большинстве (см. Haskell, где это является основной целью).

(Полное раскрытие: я функциональный программист, поэтому в качестве главного ответа вы должны взять это объяснение с небольшим количеством соли.)

Answer 8

Если вы интересуетесь этимологией (т. Е. Почему у этой концепции именно такое название), посмотрите мой пост в блоге на эту тему. Терминология происходит от философа / логика Куайна.

Answer 9

1. Denotational-семантика основана на языках моделирования путем создания доменов, которые составляют денотируемые значения.
2. Функциональные программисты используют термин " значение" для описания сходимости вычислений, основанных на правилах переписывания языка, т.е. его операционная семантика.

В 1 есть ясность двух рассматриваемых языков:

• моделируемый объектный язык
• язык моделирования, метаязык

Во 2, благодаря близости объекта и метаязыка, их можно спутать.

Как разработчик языка, я считаю, что мне нужно постоянно помнить это различие.

Профессор Редди, могу я перефразировать вас так:-)

В контексте функционального программирования и семантики термин ссылочная прозрачность не является ссылочно прозрачным.

Answer 10

Когда я прочитал принятый ответ, я подумал, что нахожусь на другой странице, а не в stackoverflow.

Ссылочная прозрачность - это более формальный способ определения чистой функции. Следовательно, если функция последовательно выдает один и тот же результат на одном и том же входе, она называется ссылочно прозрачной.

      let counter=0
function count(){
  return count++
}

это не является ссылочно прозрачным, потому что возвращаемое значение зависит от внешней переменной «counter» и продолжает меняться.

Вот как мы делаем его ссылочно прозрачным:

      function count(counter){
       return count+1
   }

Теперь эта функция стабильна и всегда возвращает один и тот же вывод, если ему предоставлен один и тот же ввод.

Answer 11

Следующий ответ, я надеюсь, добавляет и уточняет спорные 1-й и 3-й ответы.

Допустим, что выражение обозначает или ссылается на некоторый референт. Однако вопрос заключается в том, можно ли эти ссылки изоморфно кодировать как часть самих выражений, называя такие выражения "значениями". Например, значения литеральных чисел являются подмножеством набора арифметических выражений, значения истинности являются подмножеством набора логических выражений и т. Д. Идея состоит в том, чтобы вычислить выражение по его значению (если оно есть). Таким образом, слово "значение" может относиться к обозначению или к выделенному элементу набора выражений. Но если между референтом и значением существует изоморфизм (биекция), мы можем сказать, что это одно и то же. (При этом нужно быть осторожным, чтобы определить референты и изоморфизм, что доказано областью денотационной семантики. Чтобы привести пример, упомянутый в ответах на 3-й ответ, определение алгебраического типа данных data Nat = Zero | Suc Nat не соответствует ожидаемому набору натуральных чисел.)

Давайте напишем E[·] для выражения с дырой, также известной в некоторых кругах как "контекст". Два примера контекста для C-подобных выражений: [·]+1 а также[·]++,

Давайте напишем [[·]] для функции, которая принимает выражение (без дыры) и передает его значение (референт, обозначение и т. д.) в некоторый универсум, обеспечивающий смысл. (Я заимствую обозначения из области денотационной семантики.)

Давайте адаптируем определение Куайна несколько формально следующим образом: контекст E[·]является ссылочно прозрачным, если даны любые два выражения E1 а также E2 (без дырок там) так, что [[E1]] = [[E2]] (т.е. выражения обозначают / ссылаются на один и тот же референт), тогда это тот случай, когда [[E[E1]]] = [[E[E2]]] (т.е. заполнение отверстия либо E1 или же E2 приводит к выражениям, которые также обозначают одного и того же референта).

Правило Лейбница о замене равных на равных обычно выражается как "еслиE1 = E2 затем E[E1] = E[E2]', который говорит, что E[·] это функция. Функция (или, в этом отношении, программа, вычисляющая функцию) - это отображение от источника к цели, так что существует не более одного целевого элемента для каждого элемента источника. Недетерминированные функции - это неправильные числа, это либо отношения, функции, предоставляющие множества и т. Д. Если в правлении Лейбница равенство = означает, что двойные скобки просто принимаются как должное и исключаются. Таким образом, ссылочно-прозрачный контекст - это функция. И правило Лейбница является основным компонентом эквалайзерного мышления, поэтому эквалайзерное мышление определенно связано с прозрачностью ссылок.

Хотя [[·]] является функцией от выражений до обозначений, она может быть функцией от выражений до "значений", понимаемых как ограниченное подмножество выражений, и [[·]] можно понимать как оценку.

Сейчас если E1 это выражение и E2 это значение, которое у нас есть, как я думаю, подразумевается большинством людей при определении ссылочной прозрачности с точки зрения выражений, ценностей и оценки. Но, как показано в первом и третьем ответах на этой странице, это неточное определение.

Проблема с контекстами, такими как [·]++ не является побочным эффектом, но то, что его значение не определено в C изоморфно его значению. Функции не являются значениями (ну, это указатели на функции), тогда как в функциональных языках программирования они есть. Ландин, Стрейчи и пионеры денотационной семантики были достаточно умны в использовании функциональных миров для придания смысла.

Для императивных C-подобных языков мы можем (приблизительно) предоставить семантику для выражений, используя функцию [[·]] : Expression -> (State -> State x Value),

Value это подмножество Expression, State содержит пары (идентификатор, значение). Семантическая функция принимает выражение и доставляет в качестве значения функцию из текущего состояния в пару с обновленным состоянием и значением. Например, [[x]] является функцией от текущего состояния к паре, первый компонент которой является текущим состоянием, а второй компонент - значением x. По сравнению, [[x++]] является функцией от текущего состояния к паре, первый компонент которой является состоянием, в котором значение x увеличивается, а вторым компонентом является то же самое значение. В этом смысле контекст [·]++ является ссылочно прозрачным, если он удовлетворяет определению, данному выше.

Я думаю, что функциональные программисты имеют право использовать ссылочную прозрачность в том смысле, что они естественным образом восстанавливаются. [[·]] как функция от выражений к значениям. Функции являются первоклассными значениями, и состояние также может быть значением, а не обозначением. Монада состояний является (частично) чистым механизмом для передачи (или многопоточности) состояния.

Answer 12

Обратите внимание, что это понятие "смысл" происходит в сознании наблюдателя. Таким образом, одна и та же "ссылка" может означать разные вещи для разных людей. Так, например, у нас есть эдинбургская страница для устранения неоднозначности в Википедии.

Связанная проблема, которая может проявиться в контексте программирования, может быть полиморфизмом.

И, возможно, у нас должно быть название для особого случая полиморфизма (или, возможно, даже приведения), где для наших целей различные полиморфные случаи семантически эквивалентны (в отличие от просто сходства. Например, число 1 - которое может быть представлено используя целочисленный тип, или сложный тип, или любой из множества других типов - можно лечить полиморфно).

Answer 13

Ссылочная прозрачность может быть просто сформулирована как:

• Выражение, всегда оценивающее один и тот же результат в любом контексте [1],
• Функция, если заданы одни и те же параметры дважды, должна давать один и тот же результат дважды [2].

Например, язык программирования Haskell является чисто функциональным языком; Это означает, что он является прозрачным.

Answer 14

Я нашел определение ссылочной прозрачности в книге "Структура и реализация компьютерных программ" (книга мастера) полезным, потому что оно дополняется объяснением того, как ссылочная прозрачность нарушается введением операции присваивания. Проверьте следующую слайд-колоду, которую я сделал по этому вопросу: https://www.slideshare.net/pjschwarz/introducing-assignment-invalidates-the-substitution-model-of-evaluation-and-violates-referential-transparency-as-explained-in-sicp-the-wizard-book

Answer 15

Ссылочная прозрачность - это термин, используемый в компьютерных науках. Оно происходит от математической логики, но имеет широко используемое и, следовательно, верное значение в информатике.

Это означает: конструкцию (например, функцию), которую можно заменить своим результатом без изменения его значения.

В обычном использовании он похож, но не полностью эквивалентен чистым выражениям. Чистое выражение состоит исключительно из других чистых выражений. Ссылочно прозрачное выражение может быть внутренне нечистым, например, с использованием изменяемого состояния в процессе его вычисления, но не имеет побочных эффектов вне выражения в целом.

Все чистые функции, в силу их конструкции, ссылочно прозрачны, но не обязательно наоборот.

Многие языковые функции поддерживают нечеткую ссылочную прозрачность, например ST монада в Haskell и constexprs и некоторые лямбды в C++.

Иногда требуется ссылочная прозрачность, а иногда программист должен гарантировать ее самостоятельно.

Answer 16

В функциональном программировании ссылочная прозрачность обычно определяется как факт, что выражение в программе может быть заменено его значением (или чем-либо, имеющим то же значение) без изменения результата программы. Это подразумевает, что методы всегда должны возвращать одно и то же значение для данного аргумента, не оказывая никакого другого влияния. Эта концепция функционального программирования также применима к императивному программированию и может помочь вам сделать ваш код более понятным.

Ссылочная прозрачность

Выражение ссылочной прозрачности используется в различных областях, таких как математика, логика, лингвистика, философия и программирование. Это имеет совершенно разные значения в каждой из этих областей. Здесь мы будем иметь дело только с компьютерными программами, хотя мы покажем аналогию с математикой (простая математика, не волнуйтесь). Обратите внимание, однако, что ученые-компьютерщики не согласны со значением прозрачности ссылок в программировании. Мы рассмотрим ссылочную прозрачность, поскольку она используется функциональными программистами.

Ссылочная прозрачность в математике В математике ссылочная прозрачность - это свойство выражений, которое может быть заменено другими выражениями, имеющими такое же значение, без какого-либо изменения результата. Рассмотрим следующий пример:

x = 2 + (3 * 4)

Мы можем заменить подвыражение (3 * 4) любым другим выражением, имеющим такое же значение, без изменения результата (значение x). Наиболее очевидное выражение для использования, конечно, 12:

x = 2 + 12

Любое другое выражение, имеющее значение 12 (возможно (5 + 7)), может использоваться без изменения результата. Как следствие, подвыражение (3 * 4) является ссылочно прозрачным.

Мы также можем заменить выражение 2 + 12 другим выражением, имеющим такое же значение, без изменения значения x, поэтому оно также является прозрачным по ссылкам:

x = 14

Вы можете легко увидеть преимущество ссылочной прозрачности: она позволяет рассуждать. Без этого мы не могли бы разрешить любое выражение, не рассматривая некоторые другие элементы.

Ссылочная прозрачность в программировании В программировании ссылочная прозрачность применяется к программам. Поскольку программы состоят из подпрограмм, которые являются самими программами, это относится и к этим подпрограммам. Подпрограммы могут быть представлены, среди прочего, методами. Это означает, что метод может быть ссылочно прозрачным, что является случаем, если вызов этого метода может быть заменен его возвращаемым значением:

int add(int a, int b) {
        return a + b
    }

int mult(int a, int b) {
        return a * b;
    }

int x = add(2, mult(3, 4));

В этом примере метод mult ссылочно прозрачен, потому что любой вызов этого метода может быть заменен соответствующим возвращаемым значением. Это можно наблюдать, заменив mult(3, 4) на 12:

int x = add(2, 12)

Таким же образом add(2, 12) можно заменить соответствующим возвращаемым значением 14:

int x = 14;

Ни одна из этих замен не изменит результат программы, что бы она ни делала. Обратите внимание, что мы можем использовать любое другое выражение с таким же значением, что полезно при рефакторинге.

С другой стороны, рассмотрим следующую программу:

int add(int a, int b) {
    int result = a + b;
    System.out.println("Returning " + result);
    return result;
}

Замена вызова метода add на соответствующее возвращаемое значение изменит результат программы, поскольку сообщение больше не будет печататься. В этом случае это только устранит побочный эффект, но в других случаях это может изменить значение, возвращаемое методом:

public static void main(String... args) {
    printFibs(10);
}

public static void printFibs(int limit) {
    Fibs fibs = new Fibs();
    for (int i = 0; i < limit; i++) {
        System.out.println(fibs.next());
    }
}

static class Fibs {
    private int previous = -1;
    private int last = 1;

    public Integer next() {
        last = previous + (previous = last);
        return previous + last;
    }
}

Здесь следующий метод не может быть заменен чем-либо, имеющим такое же значение, так как метод предназначен для возврата разных значений при каждом вызове.

Использование таких нереферентно прозрачных методов требует строгой дисциплины, чтобы не использовать изменяемое состояние, участвующее в вычислениях. Функциональный стиль избегает таких методов в пользу ссылочно-прозрачных версий.

Ссылочная прозрачность в императивном программировании Функции императивного и функционального программирования используют. Хотя функциональное программирование использует только функции, императивное программирование использует:

• чистые функции: методы, возвращающие значения и не имеющие других эффектов
• чистые эффекты: методы, не возвращающие ничего, кроме изменения чего-либо вне их)
• функции с побочными эффектами: методы, возвращающие значение и изменяющие что-либо

Как мы все знаем, хорошей практикой является избегать функций с побочными эффектами. Это оставляет императивных программистов с чистыми функциями и чистыми эффектами. Тогда ссылочная прозрачность является мощным инструментом для императивных программистов, который упрощает анализ и тестирование их программ.

Answer 17

Ссылочная прозрачность в программировании относится к тому, когда функция получает ввод, она всегда будет возвращать одно и то же значение для заданного ввода. Взяв пример функции ниже.

      Int plusFive(int x){

return x+5

}

Функция всегда будет возвращать одно и то же значение для заданного входного целого числа x. Вывод вышеуказанной функции можно заменить возвращаемым значением, и код должен работать так же. Например, если x=10, код можно записать так:

Int output = plusFive(10)

ИЛИ

Int output = 15

Answer 18

Со страницы 176 книги « Функциональное программирование с Мирандой » Яна Холиера:

8.1 Ценности и поведение

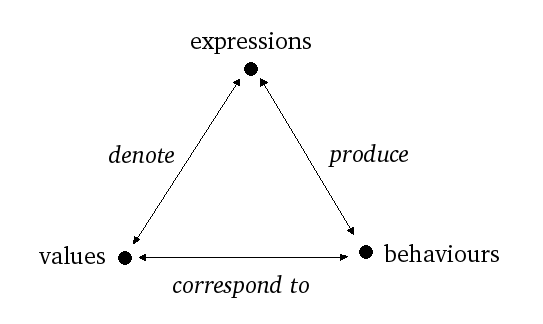
Наиболее важным свойством семантики чистого функционального языка является то, что декларативное и операционное представления языка точно совпадают следующим образом:

Этот принцип, который обычно довольно непрозрачно называют ссылочной прозрачностью , также можно изобразить следующим образом:

Условие чистоты приближает это определение к определению термина «денотативный», данному Питером Ландином в его статье «Следующие 700 языков программирования» :

Особенно,

(а) каждое выражение имеет структуру вложенного подвыражения,

(б) каждое подвыражение что-то обозначает (обычно число, значение истинности или числовую функцию),

(c) вещь, которую обозначает выражение, т. е. его «значение», зависит только от значений его подвыражений, а не от других их свойств.

... но в наши дни у вас с большей вероятностью будет реализация Haskell, которая, как отмечалось в другом месте , не считается денотативной, в значительной степени из-за ее механизма ввода-вывода:

[...] IO магический (имеет реализацию, но без обозначения) [..]

К сожалению, денотативный способ справиться с взаимодействиями вне программы остается труднодостижимым - со страницы 353 из 600 в Анатомии языков программирования Алисы Э. Фишер и Фрэнсис С. Гродзински:

В 1960-х годах несколько исследователей начали работу над доказательством того, что есть в программах. Были предприняты усилия, чтобы доказать, что:

• Программа была правильной.

• Две программы с разным кодом вычисляли одинаковые ответы при одинаковых входных данных.

• Одна программа была быстрее другой.

• Данная программа всегда завершалась.

Хотя это абстрактные цели, на самом деле все они совпадают с практической целью «отладки программы».

Становится хуже:

В результате этой работы возникло несколько сложных проблем. Одна из них заключалась в спецификации : прежде чем можно будет доказать, что программа верна, нужно указать значение слова «правильная» формально и недвусмысленно. Были разработаны формальные системы для определения смысла программы, которые подозрительно напоминали языки программирования .

^{(выделено мной.)}

... в те времена, когда «традиционные языки» были необходимы. Несомненно, такая упрямая задача сделает ее достойной Института математики Клэя ...

Мы не можем просто ждать решения - нам нужны эти веб-серверы и операционные системы сегодня . Более того, мы можем обнаружить, что решения никогда не было .

Конечно, некоторые части наших программ все еще могут быть написаны весьма знаменательно, но что касается всего остального ... необходимо практическое решение. К счастью, Ф. Уоррен Бертон описывает один из них в своей статье « Недетерминизм с ссылочной прозрачностью в языках функционального программирования» , в которой ссылочная прозрачность просто описывается как:

[...] свойство, что выражение всегда имеет одно и то же значение в одной и той же среде [...]