.Net напротив GraphicsPath.Widen()

Question

Мне нужна противоположность GraphicsPath.Widen() метод в.Net:

public GraphicsPath Widen()

Widen() Метод не принимает отрицательный параметр, поэтому мне нужен эквивалент Inset метод:

public GraphicsPath Inset()

Вы можете сделать это в приложении Inkscape с открытым исходным кодом (www.Inkscape.org), перейдя в меню и выбрав "Путь / Врезка" (количество вставок сохраняется в диалоговом окне "Свойства Inkscape"). Поскольку Inkscape является открытым исходным кодом, это должно быть возможно сделать в C#.Net, но я не могу следовать исходному коду Inkscape C++ для меня (и мне просто нужна эта одна функция, поэтому я не могу оправдать изучение C++ чтобы завершить это).

В основном мне нужен метод расширения GraphicsPath с этой подписью:

public static GraphicsPath Inset(this GraphicsPath original, float amount)
{
   //implementation
}

Как говорится в подписи, потребуется GraphicsPath объект и .Inset() путь на пройденное количество... так же, как Inkscape делает сегодня. Если это упрощает какие-либо вопросы, все графические пути создаются из .PolyBezier метод (и ничего больше), поэтому нет необходимости учитывать риты, эллипсы или любые другие формы, если вы не хотите сделать это для полноты.

К сожалению, у меня нет опыта работы с кодом C++, поэтому для меня почти невозможно следовать логике C++, содержащейся в Inkscape.

,

[РЕДАКТИРОВАТЬ:] В соответствии с просьбой, вот код Inkscape "MakeOffset". Второй параметр (double dec) будет отрицательным для Inset, а абсолютное значение этого параметра - это количество, которое нужно внести в форму.

Я знаю, что здесь много зависимостей. Если вам нужно увидеть больше исходных файлов Inkscape, они находятся здесь: http://sourceforge.net/projects/inkscape/files/inkscape/0.48/

int
Shape::MakeOffset (Shape * a, double dec, JoinType join, double miter, bool do_profile, double cx, double cy, double radius, Geom::Matrix *i2doc)
{
  Reset (0, 0);
  MakeBackData(a->_has_back_data);

    bool done_something = false;

  if (dec == 0)
  {
    _pts = a->_pts;
    if (numberOfPoints() > maxPt)
    {
      maxPt = numberOfPoints();
      if (_has_points_data) {
        pData.resize(maxPt);
        _point_data_initialised = false;
        _bbox_up_to_date = false;
        }
    }

    _aretes = a->_aretes;
    if (numberOfEdges() > maxAr)
    {
      maxAr = numberOfEdges();
      if (_has_edges_data)
    eData.resize(maxAr);
      if (_has_sweep_src_data)
        swsData.resize(maxAr);
      if (_has_sweep_dest_data)
        swdData.resize(maxAr);
      if (_has_raster_data)
        swrData.resize(maxAr);
      if (_has_back_data)
        ebData.resize(maxAr);
    }
    return 0;
  }
  if (a->numberOfPoints() <= 1 || a->numberOfEdges() <= 1 || a->type != shape_polygon)
    return shape_input_err;

  a->SortEdges ();

  a->MakeSweepDestData (true);
  a->MakeSweepSrcData (true);

  for (int i = 0; i < a->numberOfEdges(); i++)
  {
    //              int    stP=a->swsData[i].stPt/*,enP=a->swsData[i].enPt*/;
    int stB = -1, enB = -1;
    if (dec > 0)
    {
      stB = a->CycleNextAt (a->getEdge(i).st, i);
      enB = a->CyclePrevAt (a->getEdge(i).en, i);
    }
    else
    {
      stB = a->CyclePrevAt (a->getEdge(i).st, i);
      enB = a->CycleNextAt (a->getEdge(i).en, i);
    }

    Geom::Point stD, seD, enD;
    double stL, seL, enL;
    stD = a->getEdge(stB).dx;
    seD = a->getEdge(i).dx;
    enD = a->getEdge(enB).dx;

    stL = sqrt (dot(stD,stD));
    seL = sqrt (dot(seD,seD));
    enL = sqrt (dot(enD,enD));
    MiscNormalize (stD);
    MiscNormalize (enD);
    MiscNormalize (seD);

    Geom::Point ptP;
    int stNo, enNo;
    ptP = a->getPoint(a->getEdge(i).st).x;

        double this_dec;
        if (do_profile && i2doc) {
            double alpha = 1;
            double x = (Geom::L2(ptP * (*i2doc) - Geom::Point(cx,cy))/radius);
            if (x > 1) {
                this_dec = 0;
            } else if (x <= 0) {
                this_dec = dec;
            } else {
                this_dec = dec * (0.5 * cos (M_PI * (pow(x, alpha))) + 0.5);
            }
        } else {
            this_dec = dec;
        }

        if (this_dec != 0)
            done_something = true;

    int   usePathID=-1;
    int   usePieceID=0;
    double useT=0.0;
    if ( a->_has_back_data ) {
      if ( a->ebData[i].pathID >= 0 && a->ebData[stB].pathID == a->ebData[i].pathID && a->ebData[stB].pieceID == a->ebData[i].pieceID
           && a->ebData[stB].tEn == a->ebData[i].tSt ) {
        usePathID=a->ebData[i].pathID;
        usePieceID=a->ebData[i].pieceID;
        useT=a->ebData[i].tSt;
      } else {
        usePathID=a->ebData[i].pathID;
        usePieceID=0;
        useT=0;
      }
    }
    if (dec > 0)
    {
      Path::DoRightJoin (this, this_dec, join, ptP, stD, seD, miter, stL, seL,
                         stNo, enNo,usePathID,usePieceID,useT);
      a->swsData[i].stPt = enNo;
      a->swsData[stB].enPt = stNo;
    }
    else
    {
      Path::DoLeftJoin (this, -this_dec, join, ptP, stD, seD, miter, stL, seL,
                        stNo, enNo,usePathID,usePieceID,useT);
      a->swsData[i].stPt = enNo;
      a->swsData[stB].enPt = stNo;
    }
  }

  if (dec < 0)
  {
    for (int i = 0; i < numberOfEdges(); i++)
      Inverse (i);
  }

  if ( _has_back_data ) {
    for (int i = 0; i < a->numberOfEdges(); i++)
    {
      int nEd=AddEdge (a->swsData[i].stPt, a->swsData[i].enPt);
      ebData[nEd]=a->ebData[i];
    }
  } else {
    for (int i = 0; i < a->numberOfEdges(); i++)
    {
      AddEdge (a->swsData[i].stPt, a->swsData[i].enPt);
    }
  }

  a->MakeSweepSrcData (false);
  a->MakeSweepDestData (false);

  return (done_something? 0 : shape_nothing_to_do);
}

,

[Редактирует]

@ Симон Мурье - Удивительная работа. Код был даже чистым и читабельным! Хорошая работа, сэр. У меня есть пара вопросов для вас.

Во-первых, что представляет собой положительное число для суммы? Я думал, что для метода смещения положительный будет "начальным", а отрицательный будет "встроенным", но ваш пример, похоже, делает обратное.

Во-вторых, я провел базовое тестирование (просто расширил ваш пример) и обнаружил некоторые странности.

Вот то, что происходит с "l" в клёве, когда смещение увеличивается (для такого простого письма оно наверняка любит создавать проблемы!).

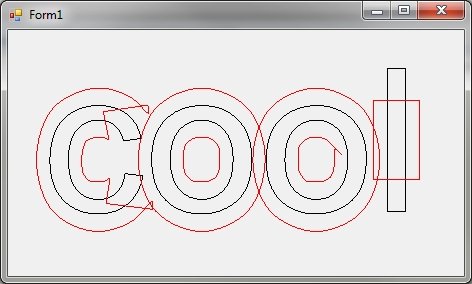
... и код для воспроизведения этого:

    private void Form1_Paint(object sender, PaintEventArgs e)
    {
            GraphicsPath path = new GraphicsPath();

            path.AddString("cool", new FontFamily("Arial"), 0, 200, new PointF(), StringFormat.GenericDefault);

            GraphicsPath offset1 = path.Offset(32);

            e.Graphics.DrawPath(new Pen(Color.Black, 1), path);
            e.Graphics.DrawPath(new Pen(Color.Red, 1), offset1);
    }

Наконец, что-то немного другое. Вот символ "S" из Wingdings (выглядит как слеза):

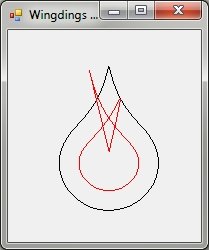
Вот код:

    private void Form1_Paint(object sender, PaintEventArgs e)
    {
        GraphicsPath path = new GraphicsPath();
        path.AddString("S", new FontFamily("Wingdings"), 0, 200, new PointF(), StringFormat.GenericDefault);
        GraphicsPath offset1 = path.Offset(20);

        e.Graphics.DrawPath(new Pen(Color.Black, 1), path);
        e.Graphics.DrawPath(new Pen(Color.Red, 1), offset1);
    }

Чувак, это так близко, что мне хочется плакать. Это все еще не работает, хотя.

Я думаю, что бы исправить это, чтобы увидеть, когда векторы врезки пересекаются, и прекратить вставку после этой точки. Если величина Inset настолько велика (или путь настолько мал), что ничего не осталось, путь должен исчезнуть (стать нулевым), вместо того, чтобы поворачиваться на себя и повторно расширяться.

Опять же, я не сбиваю с толку то, что вы сделали, но мне было интересно, знаете ли вы, что может происходить с этими примерами.

(PS - я добавил ключевое слово 'this', чтобы сделать его методом расширения, поэтому вам может понадобиться вызвать код с использованием нотации метода (параметров), чтобы эти примеры запускались)

,

@RAN Ran придумала аналогичный вывод, повторно используя собственные методы GraphicsPath. Чувак, это сложно. Оба они так близко.

Вот снимок экрана обоих примеров с использованием символа "S" из Wingdings:

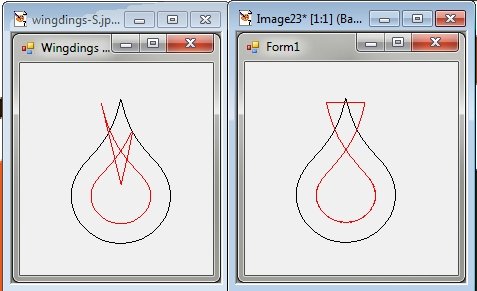
@ Симон слева, @ Ран справа.

Вот тот же символ слезы "S" после выполнения "Inset" в Inkscape. Вставка чистая:

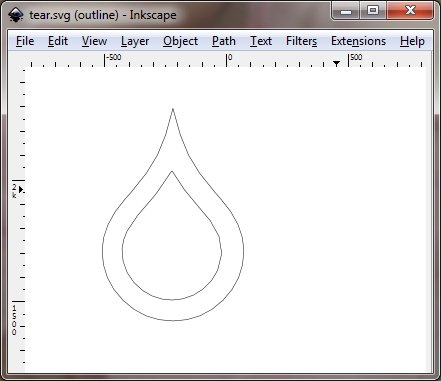
Кстати, вот код для теста @Ran:

    private void Form1_Paint(object sender, PaintEventArgs e)
    {
        GraphicsPath path = new GraphicsPath();
        path.AddString("S", new FontFamily("Wingdings"), 0, 200, new PointF(), StringFormat.GenericDefault);
        e.Graphics.DrawPath(new Pen(Color.Black, 1), path);

        GraphicsPath offset1 = path.Shrink(20);
        e.Graphics.DrawPath(new Pen(Color.Red, 1), offset1);
    }

Answer 1

Я все еще выложу свое новое решение, хотя оно и не идеальное, с некоторым списком проблем, которые необходимо исправить. Возможно, вы захотите взять его части и улучшить их, или, может быть, в этом есть некоторая ценность для обучения.

Прежде всего, картинка - моя лучшая вставка слезинки:

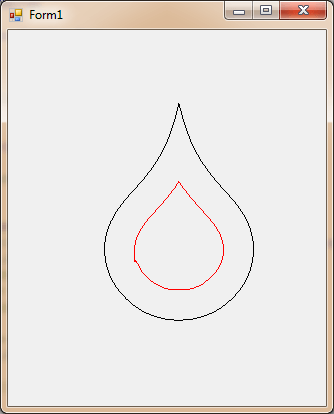
Что я сделал

1. я использовал GraphicsPath.Widen генерировать "внутренние" и "внешние" ребра данного рисунка.

2. Я отсканировал точки в результате GraphicsPath, чтобы удалить внешний край и оставить только внутренний.

3. Я сплющил внутренний край, используя GraphicsPath.Flatten так что фигуры состоят только из отрезков (без кривых).

4. Затем я отсканировал все точки на внутреннем пути и для каждого текущего сегмента:

   4.1. Если текущая точка p находится за пределами исходного пути или находится слишком близко к сегменту на исходном пути, я вычисляю новую точку на текущем ребре, которое находится на желаемом расстоянии от исходного пути, и я беру это укажите вместо p и подключите его к уже отсканированной части.

   4.2. Текущее ограничение в решении: я продолжаю с расчетной точки, чтобы продолжить сканирование. Это означает, что нет хорошей поддержки для фигур с отверстиями (например, Arial "o"). Чтобы это исправить, нужно было бы вести список "отключенных" фигур и повторно соединять фигуры, концы которых находятся в одной и той же точке (или концы, которые "достаточно близки" друг к другу).

Проблемы

Сначала я опишу основные проблемы и ограничения, а затем выложу сам код.

1. Кажется, что GraphicsPath.Widen не производит чистую форму. Внутренняя фигура, которую я получаю, имеет маленькую (но в основном невидимую) "неровность". Значение этого в том, что A) мой алгоритм отбора генерирует больше шума, а B) на рисунке больше точек, поэтому производительность ухудшается.

2. Производительность едва ли приемлема, если вообще, на данном этапе. Мое решение в настоящее время сканирует очень наивным способом (в O (n ^ n)), чтобы найти отрезки линий, которые "слишком близки" к точкам-кандидатам на внутреннем крае. Это приводит к тому, что алгоритм работает очень медленно. Это можно улучшить, поддерживая некоторую структуру данных, в которой сегменты сортируются по x, так что количество вычислений расстояния значительно сокращается.

3. Я не удосужился оптимизировать код для использования structs и во многих других местах код можно оптимизировать, чтобы он был намного быстрее.

4. Не существует поддержки для фигур с отверстиями, где внутренняя фигура должна "делиться" на несколько фигур (например, Arial "o"). Я знаю, как это реализовать, но на это нужно больше времени:)

5. Я бы подумал об адаптации подхода Саймона к перемещению существующих точек, чтобы получить внутреннюю фигуру, с моим подходом, чтобы очистить этот путь. (Но я не мог сделать это на данный момент из-за ошибки в решении Саймона, которая, например, приводит к смещению заостренного конца символа "Слеза" в допустимое местоположение внутри фигуры. Мой алгоритм считает, что это местоположение допустимо и не убирает это).

Код

Я не мог не придумать свои собственные математические / геометрические утилиты. Так вот код...

Лично я думаю, что это может быть достойно награды, даже если это не идеальное решение...:)

public class LineSegment
{
    private readonly LineEquation line;
    private RectangleF bindingRectangle;

    public PointF A { get; private set; }
    public PointF B { get; private set; }

    public LineSegment(PointF a, PointF b)
    {
        A = a;
        B = b;

        line = new LineEquation(a, b);
        bindingRectangle = new RectangleF(
            Math.Min(a.X, b.X), Math.Min(a.Y, b.Y), 
            Math.Abs(a.X - b.X), Math.Abs(a.Y - b.Y));
    }

    public PointF? Intersect(LineSegment other)
    {
        var p = line.Intersect(other.line);
        if (p == null) return null;

        if (bindingRectangle.Contains(p.Value) &&
            other.bindingRectangle.Contains(p.Value))
        {
            return p;
        }
        return null;
    }

    public float Distance(PointF p)
    {
        if (LineEquation.IsBetween(line.GetNormalAt(A), p, line.GetNormalAt(B)))
        {
            return line.Distance(p);
        }
        return Math.Min(Distance(A, p), Distance(B, p));

    }

    static float Distance(PointF p1, PointF p2)
    {
        var x = p1.X - p2.X;
        var y = p1.Y - p2.Y;
        return (float) Math.Sqrt(x*x + y*y);
    }

    public PointF? IntersectAtDistance(LineSegment segmentToCut, float width)
    {
        // always assuming other.A is the farthest end
        var distance = width* (line.IsAboveOrRightOf(segmentToCut.A) ? 1 : -1);
        var parallelLine = line.GetParallelLine(distance);

        var p = parallelLine.Intersect(segmentToCut.line);
        if (p.HasValue)
        {
            if (LineEquation.IsBetween(line.GetNormalAt(A), p.Value, line.GetNormalAt(B)) &&
                segmentToCut.bindingRectangle.Contains(p.Value))
            {
                return p;
            }
        }

        List<PointF> points = new List<PointF>();
        points.AddRange(segmentToCut.line.Intersect(new CircleEquation(width, A)));
        points.AddRange(segmentToCut.line.Intersect(new CircleEquation(width, B)));

        return GetNearestPoint(segmentToCut.A, points);
    }

    public static PointF GetNearestPoint(PointF p, IEnumerable<PointF> points)
    {
        float minDistance = float.MaxValue;
        PointF nearestPoint = p;
        foreach (var point in points)
        {
            var d = Distance(p, point);
            if (d < minDistance)
            {
                minDistance = d;
                nearestPoint = point;
            }
        }
        return nearestPoint;
    }
}

public class LineEquation
{
    private readonly float a;
    private readonly float b;

    private readonly bool isVertical;
    private readonly float xConstForVertical;

    public LineEquation(float a, float b)
    {
        this.a = a;
        this.b = b;
        isVertical = false;
    }

    public LineEquation(float xConstant)
    {
        isVertical = true;
        xConstForVertical = xConstant;
    }

    public LineEquation(float a, PointF p)
    {
        this.a = a;
        b = p.Y - a*p.X;
        isVertical = false;
    }

    public LineEquation(PointF p1, PointF p2)
    {
        if (p1.X == p2.X)
        {
            isVertical = true;
            xConstForVertical = p1.X;
            return;
        }

        a = (p1.Y - p2.Y)/(p1.X - p2.X);
        b = p1.Y - a * p1.X;
        isVertical = false;
    }

    public PointF? Intersect(float x)
    {
        if (isVertical)
        {
            return null;
        }
        return new PointF(x, a*x + b);
    }

    public PointF? Intersect(LineEquation other)
    {
        if (isVertical && other.isVertical) return null;
        if (a == other.a) return null;

        if (isVertical) return other.Intersect(xConstForVertical);
        if (other.isVertical) return Intersect(other.xConstForVertical);

        // both have slopes and are not parallel
        var x = (b - other.b) / (other.a - a);
        return Intersect(x);
    }

    public float Distance(PointF p)
    {
        if (isVertical)
        {
            return Math.Abs(p.X - xConstForVertical);
        }
        var p1 = Intersect(0).Value;
        var p2 = Intersect(100).Value;

        var x1 = p.X - p1.X;
        var y1 = p.Y - p1.Y;
        var x2 = p2.X - p1.X;
        var y2 = p2.Y - p1.Y;

        return (float) (Math.Abs(x1*y2 - x2*y1) / Math.Sqrt(x2*x2 + y2*y2));
    }

    public bool IsAboveOrRightOf(PointF p)
    {
        return isVertical ? 
            xConstForVertical > p.X : 
            a*p.X + b > p.Y;
    }

    public static bool IsBetween(LineEquation l1, PointF p, LineEquation l2)
    {
        return l1.IsAboveOrRightOf(p) ^ l2.IsAboveOrRightOf(p);
    }

    public LineEquation GetParallelLine(float distance)
    {
        if (isVertical) return new LineEquation(xConstForVertical + distance);

        var angle = Math.Atan(a);
        float dy = (float) (distance/Math.Sin(angle));
        return new LineEquation(a, b - dy);
    }

    public LineEquation GetNormalAt(PointF p)
    {
        if (isVertical) return new LineEquation(p.X);

        var newA = -1/a;
        var newB = (a + 1/a)*p.X + b;
        return new LineEquation(newA, newB);
    }

    public PointF[] Intersect(CircleEquation circle)
    {
        var cx = circle.Center.X;
        var cy = circle.Center.Y;
        var r = circle.Radius;

        if (isVertical)
        {
            var distance = Math.Abs(cx - xConstForVertical);
            if (distance > r) return new PointF[0];
            if (distance == r) return new[] {new PointF(xConstForVertical, cy) };

            // two intersections
            var dx = cx - xConstForVertical;

            var qe = new QuadraticEquation(
                1,
                -2 * cy,
                r * r - dx * dx);

            return qe.Solve();
        }

        var t = b - cy;
        var q = new QuadraticEquation(
            1 + a*a,
            2*a*t - 2*cx,
            cx*cx + t*t - r*r);

        var solutions = q.Solve();
        for (var i = 0; i < solutions.Length; i++) 
           solutions[i] = Intersect(solutions[i].X).Value;
        return solutions;
    }
}

public class CircleEquation
{
    public float Radius { get; private set; }
    public PointF Center { get; private set; }

    public CircleEquation(float radius, PointF center)
    {
        Radius = radius;
        Center = center;
    }
}

public class QuadraticEquation
{
    public float A { get; private set; }
    public float B { get; private set; }
    public float C { get; private set; }

    public QuadraticEquation(float a, float b, float c)
    {
        A = a;
        B = b;
        C = c;
    }

    public PointF Intersect(float x)
    {
        return new PointF(x, A*x*x + B*x + C);
    }
    public PointF[] Solve()
    {
        var d = B*B - 4*A*C;
        if (d < 0) return new PointF[0];
        if (d == 0)
        {
            var x = -B / (2*A);
            return new[] { Intersect(x) };
        }

        var sd = Math.Sqrt(d);
        var x1 = (float) ((-B - sd) / (2f*A));
        var x2 = (float) ((-B + sd) / (2*A));
        return new[] { Intersect(x1), Intersect(x2) };
    }
}

public static class GraphicsPathExtension
{
    public static GraphicsPath Shrink(this GraphicsPath originalPath, float width)
    {
        originalPath.CloseAllFigures();
        originalPath.Flatten();
        var parts = originalPath.SplitFigures();
        var shrunkPaths = new List<GraphicsPath>();

        foreach (var part in parts)
        {
            using (var widePath = new GraphicsPath(part.PathPoints, part.PathTypes))
            {
                // widen the figure
                widePath.Widen(new Pen(Color.Black, width * 2));

                // pick the inner edge
                var innerEdge = widePath.SplitFigures()[1];
                var fixedPath = CleanPath(innerEdge, part, width);
                if (fixedPath.PointCount > 0)
                    shrunkPaths.Add(fixedPath);
            }
        }

        // build the result
        originalPath.Reset();
        foreach (var p in shrunkPaths)
        {
            originalPath.AddPath(p, false);
        }
        return originalPath;
    }

    public static IList<GraphicsPath> SplitFigures(this GraphicsPath path)
    {
        var paths = new List<GraphicsPath>();
        var position = 0;
        while (position < path.PointCount)
        {
            var figureCount = CountNextFigure(path.PathData, position);

            var points = new PointF[figureCount];
            var types = new byte[figureCount];

            Array.Copy(path.PathPoints, position, points, 0, figureCount);
            Array.Copy(path.PathTypes, position, types, 0, figureCount);
            position += figureCount;

            paths.Add(new GraphicsPath(points, types));
        }
        return paths;
    }

    static int CountNextFigure(PathData data, int position)
    {
        var count = 0;
        for (var i = position; i < data.Types.Length; i++)
        {
            count++;
            if (0 != (data.Types[i] & (int)PathPointType.CloseSubpath))
            {
                return count;
            }
        }
        return count;
    }

    static GraphicsPath CleanPath(GraphicsPath innerPath, GraphicsPath originalPath, float width)
    {
        var points = new List<PointF>();
        Region originalRegion = new Region(originalPath);

        // find first valid point
        int firstValidPoint = 0;
        IEnumerable<LineSegment> segs;

        while (IsPointTooClose(
                   innerPath.PathPoints[firstValidPoint], 
                   originalPath, originalRegion, width, out segs))
        {
            firstValidPoint++;
            if (firstValidPoint == innerPath.PointCount) return new GraphicsPath();
        }

        var prevP = innerPath.PathPoints[firstValidPoint];
        points.Add(prevP);

        for (int i = 1; i < innerPath.PointCount; i++)
        {
            var p = innerPath.PathPoints[(firstValidPoint + i) % innerPath.PointCount];

            if (!IsPointTooClose(p, originalPath, originalRegion, width, out segs))
            {
                prevP = p;
                points.Add(p);
                continue;
            }

            var invalidSegment = new LineSegment(prevP, p);

            // found invalid point (too close or external to original figure)
            IEnumerable<PointF> cutPoints = 
                segs.Select(seg => seg.IntersectAtDistance(invalidSegment, width).Value);
            var cutPoint = LineSegment.GetNearestPoint(prevP, cutPoints);

            // now add the cutPoint instead of 'p'.
            points.Add(cutPoint);
            prevP = cutPoint;
        }

        var types = new List<byte>();
        for (int i = 0; i < points.Count - 1; i++)
        {
            types.Add(1);
        }
        types.Add(129);

        return points.Count == 0 ?
            new GraphicsPath() :
            new GraphicsPath(points.ToArray(), types.ToArray());
    }

    static bool IsPointTooClose(
        PointF p, GraphicsPath path, Region region, 
        float distance, out IEnumerable<LineSegment> breakingSegments)
    {
        if (!region.IsVisible(p))
        {
            breakingSegments = new LineSegment[0];
            return true;
        }

        var segs = new List<LineSegment>();
        foreach (var seg in GetSegments(path))
        {
            if (seg.Distance(p) < distance)
            {
                segs.Add(seg);
            }
        }
        breakingSegments = segs;
        return segs.Count > 0;
    }

    static public IEnumerable<LineSegment> GetSegments(GraphicsPath path)
    {
        for (var i = 0; i < path.PointCount; i++)
        {
            yield return 
                new LineSegment(path.PathPoints[i], path.PathPoints[(i + 1) % path.PointCount]);
        }
    }
}

Answer 2

Вот хорошая альтернатива. Он не такой сложный, как у @Simon's, но он дает хорошие результаты (которые можно еще улучшить) с гораздо более простым кодом.

Идея состоит в том, чтобы повторно использовать существующую функциональность GraphicsPath.Widen для того, чтобы получить очки.

Когда мы звоним Widen на GraphicsPath который состоит из n замкнутых фигур, результирующий путь имеет 2n ребер. Внешний и внутренний край для каждой оригинальной фигуры.

Итак, я создаю временный путь, расширяю его и копирую только внутренние края.

Вот код:

public static GraphicsPath Shrink(this GraphicsPath path, float width)
{
    using (var p = new GraphicsPath())
    {
        p.AddPath(path, false);
        p.CloseAllFigures();
        p.Widen(new Pen(Color.Black, width*2));

        var position = 0;
        var result = new GraphicsPath();
        while (position < p.PointCount)
        {
            // skip outer edge
            position += CountNextFigure(p.PathData, position);
            // count inner edge
            var figureCount = CountNextFigure(p.PathData, position);
            var points = new PointF[figureCount];
            var types = new byte[figureCount];

            Array.Copy(p.PathPoints, position, points, 0, figureCount);
            Array.Copy(p.PathTypes, position, types, 0, figureCount);
            position += figureCount;
            result.AddPath(new GraphicsPath(points, types), false);
        }
        path.Reset();
        path.AddPath(result, false);
        return path;
    }
}

static int CountNextFigure(PathData data, int position)
{
    int count = 0;
    for (var i = position; i < data.Types.Length; i++)
    {
        count++;
        if (0 != (data.Types[i] & (int) PathPointType.CloseSubpath))
        {
            return count;
        }
    }
    return count;
}

И вот пример:

GraphicsPath path = new GraphicsPath();
path.AddString("cool", new FontFamily("Times New Roman"), 0, 300, 
    new PointF(), StringFormat.GenericDefault);
e.Graphics.DrawPath(new Pen(Color.Black, 1), path); 
path.Shrink(3);
e.Graphics.DrawPath(new Pen(Color.Red), path);

По общему признанию, мое решение также имеет нежелательные артефакты, когда смещение достаточно велико, чтобы заставить форму пересекаться с собой.

РЕДАКТИРОВАТЬ:

Я могу легко обнаружить все точки пересечения в O (n ^ 2), или с некоторым усилием - обнаружить их в O (n logn), используя алгоритм линии развертки (n - это число точек).

Но как только я нашел точки пересечения, я не уверен, как решить, какие части пути удалить. У кого-нибудь есть идея?:)

РЕДАКТИРОВАТЬ 2:

На самом деле нам не нужно находить пересечения фигур.

Что мы можем сделать, это отсканировать все точки на рисунке. Как только мы нашли точку, которая находится за пределами исходной фигуры или слишком близко к краю исходной фигуры, мы должны это исправить.

Чтобы зафиксировать точку, мы смотрим на край между этой точкой и предыдущей, и нам нужно обрезать этот край, чтобы он теперь заканчивался в новой точке на правильном расстоянии от исходной фигуры.

Я провел несколько экспериментов с приближенным к этому алгоритму (с грубым, но простым алгоритмом, в котором я полностью удалял "точки отключения" вместо того, чтобы перемещать их, чтобы сократить их край, и я проверял расстояния до точек на исходной фигуре вместо того, чтобы края на это). Это дало хорошие результаты удаления большинства нежелательных артефактов.

Для реализации полного решения, вероятно, потребуется несколько часов...

РЕДАКТИРОВАТЬ 3:

Хотя я все еще далек от совершенства, я разместил свое улучшенное решение в отдельном ответе.

Answer 3

Вот код, который, кажется, работает. Он поддерживает закрытые и открытые цифры (это сложная часть...), положительные и отрицательные смещения.

По сути, в каждой точке пути вычисляется точка смещения. Точка смещения определяется с использованием вектора нормали, но на самом деле она рассчитывается с использованием пересечения двух линий смещения (что эквивалентно). В некоторых случаях это не будет отображаться красиво (если фрагменты пути расположены слишком близко, например, ближе, чем смещение).

Обратите внимание, что он не объединяет / объединяет смещения для пересекающихся фигур, но это другая история. Теоретическую статью можно найти здесь: Алгоритм смещения для полилинейных кривых.

Вы можете попробовать это с этим примером:

protected override void OnPaint(PaintEventArgs e)
{
    GraphicsPath path = new GraphicsPath();

    path.AddString("cool", new FontFamily("Arial"), 0, 200, new PointF(), StringFormat.GenericDefault);
    path.AddEllipse(150, 50, 80, 80);
    path.AddEllipse(150 + 100, 50 + 100, 80 + 100, 80 + 100);

    GraphicsPath offset1 = Offset(path, -5);
    GraphicsPath offset2 = Offset(path, 5);

    e.Graphics.DrawPath(new Pen(Color.Black, 1), path);
    e.Graphics.DrawPath(new Pen(Color.Red, 1), offset1);
    e.Graphics.DrawPath(new Pen(Color.Blue, 1), offset2);
}

Полный код:

public static GraphicsPath Offset(GraphicsPath path, float offset)
{
    if (path == null)
        throw new ArgumentNullException("path");

    // death from natural causes
    if (path.PointCount < 2)
        throw new ArgumentException(null, "path");

    PointF[] points = new PointF[path.PointCount];

    for (int i = 0; i < path.PointCount; i++)
    {
        PointF current = path.PathPoints[i];
        PointF prev = GetPreviousPoint(path, i);
        PointF next = GetNextPoint(path, i);

        PointF offsetPoint = Offset(prev, current, next, offset);
        points[i] = offsetPoint;
    }

    GraphicsPath newPath = new GraphicsPath(points, path.PathTypes);
    return newPath;
}

// get the closing point for a figure or null if none was found
private static PointF? GetClosingPoint(GraphicsPath path, ref int index)
{
    for (int i = index + 1; i < path.PointCount; i++)
    {
        if (IsClosingPoint(path, i))
        {
            index = i;
            return path.PathPoints[i];
        }
    }
    return null;
}

// get the starting point for a figure or null if none was found
private static PointF? GetStartingPoint(GraphicsPath path, ref int index)
{
    for (int i = index - 1; i >= 0; i--)
    {
        if (IsStartingPoint(path, i))
        {
            index = i;
            return path.PathPoints[i];
        }
    }
    return null;
}

// get a previous point to compute normal vector at specified index
private static PointF GetPreviousPoint(GraphicsPath path, int index)
{
    if (IsStartingPoint(path, index))
    {
        int closingIndex = index;
        PointF? closing = GetClosingPoint(path, index, ref closingIndex);
        if (closing.HasValue)
        {
            if (closing.Value != path.PathPoints[index])
                return closing.Value;

            return GetPreviousPoint(path, closingIndex);
        }
    }
    else
    {
        return path.PathPoints[index - 1];
    }

    // we are on an unclosed end point, emulate a prev point on the same line using next point
    PointF point = path.PathPoints[index];
    PointF next = path.PathPoints[index + 1];
    return VectorF.Add(point, VectorF.Substract(point, next));
}

// get a next point to compute normal vector at specified index
private static PointF GetNextPoint(GraphicsPath path, int index)
{
    if (IsClosingPoint(path, index))
    {
        int startingIndex = index;
        PointF? starting = GetStartingPoint(path, ref startingIndex);
        if (starting.HasValue)
        {
            // some figures (Ellipse) are closed with the same point as the starting point
            // in this case, we need the starting point's next point
            if (starting.Value != path.PathPoints[index])
                return starting.Value;

            return GetNextPoint(path, startingIndex);
        }
    }
    else if ((index != (path.PointCount - 1)) && (!IsStartingPoint(path, index + 1)))
    {
        return path.PathPoints[index + 1];
    }

    // we are on an unclosed end point, emulate a next point on the same line using previous point
    PointF point = path.PathPoints[index];
    PointF prev = path.PathPoints[index - 1];
    return VectorF.Add(point, VectorF.Substract(point, prev));
}

// determine if a point is a closing point
private static bool IsClosingPoint(GraphicsPath path, int index)
{
    return (path.PathTypes[index] & (byte)PathPointType.CloseSubpath) == (byte)PathPointType.CloseSubpath;
}

// determine if a point is a starting point
private static bool IsStartingPoint(GraphicsPath path, int index)
{
    return (path.PathTypes[index] == (byte)PathPointType.Start);
}

// offsets a Point using the normal vector (actually computed using intersection or 90° rotated vectors)
private static PointF Offset(PointF prev, PointF current, PointF next, float offset)
{
    VectorF vnext = VectorF.Substract(next, current);
    vnext = vnext.DegreeRotate(Math.Sign(offset) * 90);
    vnext = vnext.Normalize() * Math.Abs(offset);
    PointF pnext1 = current + vnext;
    PointF pnext2 = next + vnext;

    VectorF vprev = VectorF.Substract(prev, current);
    vprev = vprev.DegreeRotate(-Math.Sign(offset) * 90);
    vprev = vprev.Normalize() * Math.Abs(offset);
    PointF pprev1 = current + vprev;
    PointF pprev2 = prev + vprev;

    PointF ix = VectorF.GetIntersection(pnext1, pnext2, pprev1, pprev2);
    if (ix.IsEmpty)
    {
        // 3 points on the same line, just translate (both vectors are identical)
        ix = current + vnext;
    }
    return ix;
}

// a useful Vector class (does not exists in GDI+, why?)
[Serializable, StructLayout(LayoutKind.Sequential)]
public struct VectorF : IFormattable, IEquatable<VectorF>
{
    private float _x;
    private float _y;

    public VectorF(float x, float y)
    {
        _x = x;
        _y = y;
    }

    public float X
    {
        get
        {
            return _x;
        }
        set
        {
            _x = value;
        }
    }

    public float Y
    {
        get
        {
            return _y;
        }
        set
        {
            _y = value;
        }
    }

    public double Length
    {
        get
        {
            return Math.Sqrt(_x * _x + _y * _y);
        }
    }

    public VectorF Rotate(double angle)
    {
        float cos = (float)Math.Cos(angle);
        float sin = (float)Math.Sin(angle);
        return new VectorF(_x * cos - _y * sin, _x * sin + _y * cos);
    }

    public VectorF DegreeRotate(double angle)
    {
        return Rotate(DegreeToGradiant(angle));
    }

    public static PointF GetIntersection(PointF start1, PointF end1, PointF start2, PointF end2)
    {
        float denominator = ((end1.X - start1.X) * (end2.Y - start2.Y)) - ((end1.Y - start1.Y) * (end2.X - start2.X));
        if (denominator == 0) // parallel
            return PointF.Empty;

        float numerator = ((start1.Y - start2.Y) * (end2.X - start2.X)) - ((start1.X - start2.X) * (end2.Y - start2.Y));
        float r = numerator / denominator;

        PointF result = new PointF();
        result.X = start1.X + (r * (end1.X - start1.X));
        result.Y = start1.Y + (r * (end1.Y - start1.Y));
        return result;
    }

    public static PointF Add(PointF point, VectorF vector)
    {
        return new PointF(point.X + vector._x, point.Y + vector._y);
    }

    public static VectorF Add(VectorF vector1, VectorF vector2)
    {
        return new VectorF(vector1._x + vector2._x, vector1._y + vector2._y);
    }

    public static VectorF Divide(VectorF vector, float scalar)
    {
        return vector * (1.0f / scalar);
    }

    public static VectorF Multiply(float scalar, VectorF vector)
    {
        return new VectorF(vector._x * scalar, vector._y * scalar);
    }

    public static VectorF Multiply(VectorF vector, float scalar)
    {
        return Multiply(scalar, vector);
    }

    public static VectorF operator *(float scalar, VectorF vector)
    {
        return Multiply(scalar, vector);
    }

    public static VectorF operator *(VectorF vector, float scalar)
    {
        return Multiply(scalar, vector);
    }

    public static PointF operator -(PointF point, VectorF vector)
    {
        return Substract(point, vector);
    }

    public static PointF operator +(VectorF vector, PointF point)
    {
        return Add(point, vector);
    }

    public static PointF operator +(PointF point, VectorF vector)
    {
        return Add(point, vector);
    }

    public static VectorF operator +(VectorF vector1, VectorF vector2)
    {
        return Add(vector1, vector2);
    }

    public static VectorF operator /(VectorF vector, float scalar)
    {
        return Divide(vector, scalar);
    }

    public static VectorF Substract(PointF point1, PointF point2)
    {
        return new VectorF(point1.X - point2.X, point1.Y - point2.Y);
    }

    public static PointF Substract(PointF point, VectorF vector)
    {
        return new PointF(point.X - vector._x, point.Y - vector._y);
    }

    public static double AngleBetween(VectorF vector1, VectorF vector2)
    {
        double y = (vector1._x * vector2._y) - (vector2._x * vector1._y);
        double x = (vector1._x * vector2._x) + (vector1._y * vector2._y);
        return Math.Atan2(y, x);
    }

    private static double GradiantToDegree(double angle)
    {
        return (angle * 180) / Math.PI;
    }

    private static double DegreeToGradiant(double angle)
    {
        return (angle * Math.PI) / 180;
    }

    public static double DegreeAngleBetween(VectorF vector1, VectorF vector2)
    {
        return GradiantToDegree(AngleBetween(vector1, vector2));
    }

    public VectorF Normalize()
    {
        if (Length == 0)
            return this;

        VectorF vector = this / (float)Length;
        return vector;
    }

    public override string ToString()
    {
        return ToString(null, null);
    }

    public string ToString(string format, IFormatProvider provider)
    {
        return string.Format(provider, "{0:" + format + "};{1:" + format + "}", _x, _y);
    }

    public override int GetHashCode()
    {
        return _x.GetHashCode() ^ _y.GetHashCode();
    }

    public override bool Equals(object obj)
    {
        if ((obj == null) || !(obj is VectorF))
            return false;

        return Equals(this, (VectorF)obj);
    }

    public bool Equals(VectorF value)
    {
        return Equals(this, value);
    }

    public static bool Equals(VectorF vector1, VectorF vector2)
    {
        return (vector1._x.Equals(vector2._x) && vector1._y.Equals(vector2._y));
    }
}

Answer 4

Хорошо, я думаю, что у меня есть преимущество для вас, ребята... но это совершенно другое направление.

Во всяком случае, я понял, что "подпуть" большего пути на самом деле сжимается (вставки) во время .Widen операция, поэтому я решил посмотреть, есть ли что-нибудь плодотворное на этом пути (не каламбур).

На самом деле, идея здесь заключается в .Widen путь... снаружи!

Что делать, если мы взяли оригинал GraphicsPath и "завернул" его в больший Rectangle (делает Inflate из 10 на .GetBounds из GraphicsPath должен достать нам легкую обертку).

Затем сначала добавляется обертка, а реальная GraphicsPath добавляется как подпуть к этому. Вся вещь тогда получает .Widenи, наконец, новый GraphicsPath создается с нуля, используя .PathPoints а также .PathTypes расширенного пути, который удаляет ненужную обертку (к счастью, GraphicsPath принимает PathPoints а также PathTypes в одной из перегрузок конструктора).

Я буду вне офиса до конца дня, так что я не могу довести это до конца, но в этом вся суть.

Просто поместите этот код в обычную форму:

        private void Form1_Paint(object sender, PaintEventArgs e)
        {
            GraphicsPath g = new GraphicsPath();
            g.AddRectangle(new Rectangle(0, 0, 200, 200));
            g.AddEllipse(50, 50, 100, 100);

            //Original path
            e.Graphics.DrawPath(new Pen(Color.Black,2), g);

            //"Inset" path
            g.Widen(new Pen(Color.Black, 10));
            e.Graphics.DrawPath(new Pen(Color.Red, 2), g);
        }

Из этого простого эксперимента вы увидите, что целевой путь (круг) теперь имеет неуловимую вставку (красного цвета)!

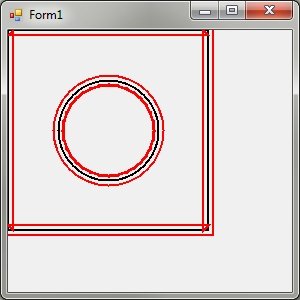
Там также есть какая-то другая ерунда, которую я не совсем понимаю там (которая также появляется на обертке прямоугольника), но из PathPoints а также PathTypes, должна быть возможность выполнять итерацию массивов и удалять ненужные файлы при создании virgin GraphicsPath (или выяснить, откуда поступил этот ненужный файл и предотвратить его возникновение). Затем верните новый, чистый GraphicsPath,

Эта техника избегает всей сложной математики, но это немного далеко.