Логический вывод с системой Fitch

Question

Я работал с некоторой логикой, и я нашел трудность, которую не могу решить,

Как я могу доказать из предпосылки p=>q, что ¬q=>¬p?

Спасибо

Answer 1

Тонкая настройка с удалением лишнего шага:

Использование системы Fitch:

1. р => д............ Предпосылка
2. | ¬q............ Успенская
3. |. | р............ Успенская
4. |. | ¬q............ повтор: 2
5. | p => ¬q............ Импликация Введение: 4
6. | ¬p............ Отрицание Введение: 1,5
7. ¬q => ¬p............ Последствия Введение: 6

Answer 2

Использование системы Fitch:

1. р => д............ Предпосылка
2. . | ¬q............ Успенская
3. . |. | р............ Успенская
4. . |. | q............ Устранение последствий: 1,3
5. . |. | ¬q............ повтор: 2
6. . | p => ¬q............ Импликация Введение: 5
7. . | ¬p............ Отрицание Введение: 1,6
8. ¬q => ¬p............ Последствия Введение: 7

Не такой аккуратный макет, но каждый "отступ" представляет собой подзаказы, сделанные с помощью предположений.

Answer 3

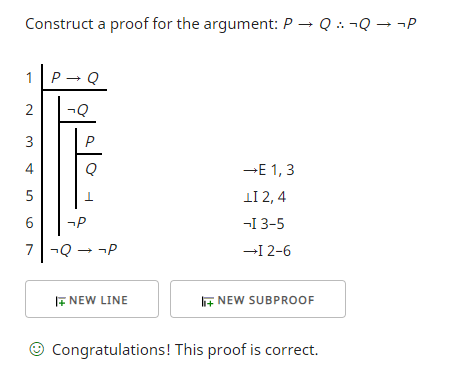
Вот доказательство с использованием проверки в стиле Fitch. Пояснения к правилам находятся в forallx. Обе ссылки доступны онлайн и перечислены ниже:

---

Ссылка

Редактор и средство проверки естественных дедукций Кевина Клемента в стиле JavaScript/PHP Fitch http://proofs.openlogicproject.org/

П.Д. Магнус, Тим Баттон с дополнениями Дж. Роберта Лофтиса, ремикс и рецензия Аарона Томаса-Болдука, Ричарда Зака, forallx Калгари Ремикс: Введение в формальную логику, зима 2018. http://forallx.openlogicproject.org/