Как запланировать различные типы досок для формирования мостов

Question

Предположим, мы хотим пройти от места $A$ до места $B$, но между ними есть несколько рек. Чтобы пройти от места $A$ к месту $B$, нам нужно построить мост для каждой реки.

У нас есть несколько видов досок. Различные типы досок имеют разную стоимость и длину, но одинаковые типы досок имеют одинаковую стоимость и длину. Мы можем использовать доски для строительства мостов. Однако количество доступных досок ограничено. Наша цель - построить мост для каждой реки, одновременно сводя к минимуму общую стоимость досок.

Чтобы лучше описать проблему, мы нарисуем фигуру, чтобы описать нашу проблему.

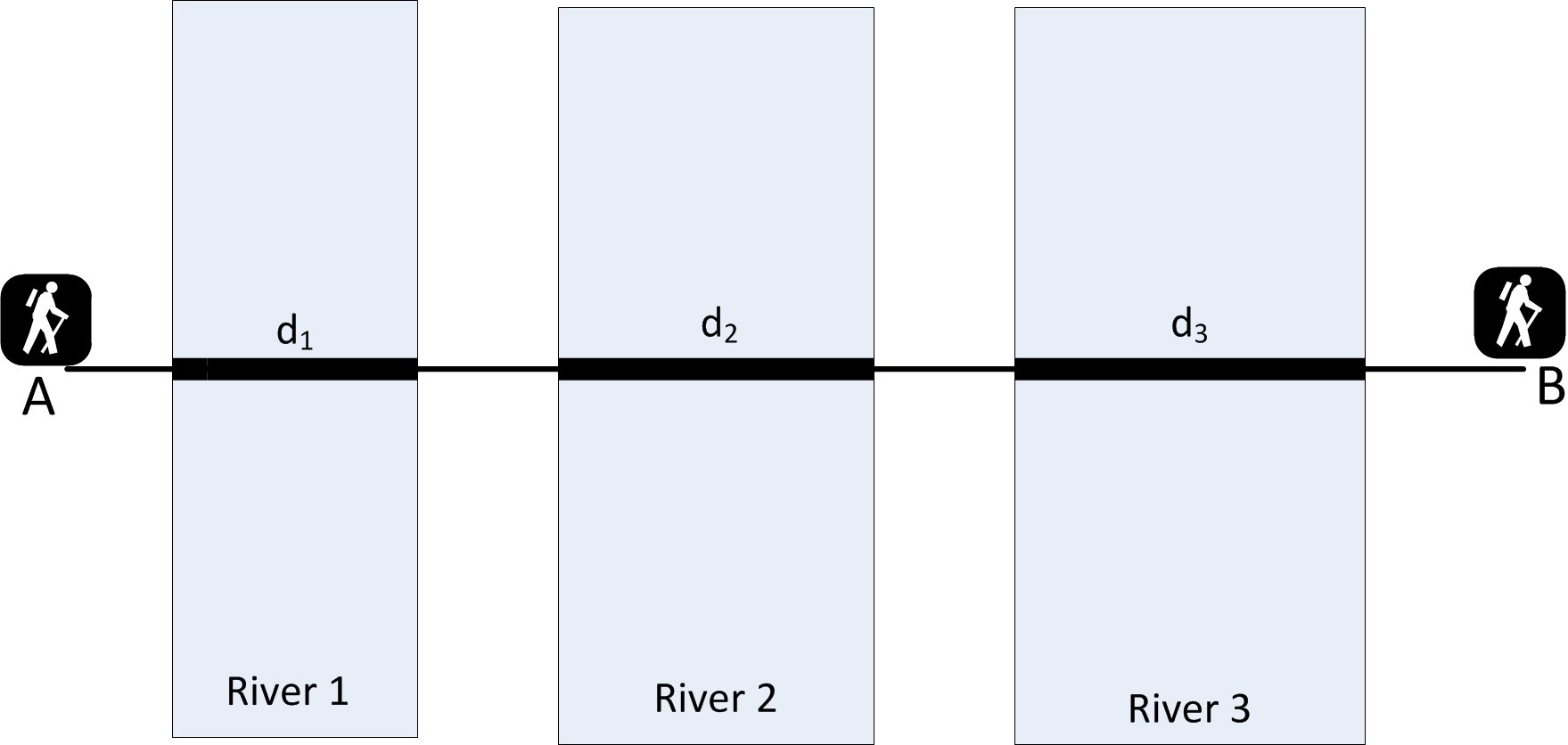
В трех реках длина мостов составляет $ d_1 $, $ d_2 $ и $ d_3 $ соответственно.

У нас есть $4$ типов досок. Пусть $ l_i $ и $ c_i $ обозначают длину и стоимость планки $ i $ -го типа. Пусть $\delta_i$ обозначает доступное количество досок $ i $ -го типа. Пусть $n_{ij}$ обозначает количество досок, используемых для построения моста $j$.

Тогда проблема может быть сформулирована следующим образом:

Минимизируйте $\sum_{j=1}^3 \sum_{i=1}^4 n_{ij}c_i$

улица

$ \ sum_ {i = 1} ^ 4 n_ {ij} l_i \ geq d_j $

$ \ sum_ {j = 1} ^ 3 n_ {ij} \ leq \ delta_i $

$ n_ {ij} \ geq 0 $ & $ n_ {ij} \ in Z $

Я думаю, что эта проблема должна быть NP-Hard, так как это целочисленная проблема программирования. Это правда? кто-нибудь знает, как решить эту проблему? Даже решение, которое не является оптимальным.

Answer 1

Если вы можете разделить планки и использовать элементы на нескольких мостах, и вы можете использовать планки разных типов на одном мосту, это не является NP-завершенным, потому что вы сначала используете самую дешевую планку на метр и продолжаете.

В противном случае он, вероятно, является NP-полным, потому что это тоже проблема упаковки бункера. Например, если вы не можете разделить доски, чтобы использовать части на нескольких мостах, предположим, что у вас есть этот набор данных:

• Река 1 имеет разрыв 7 метров
• Река 2 имеет разрыв 6 метров

С досками:

• 10 досок по 7 метров каждая. Цена: 60 ​​$ за доску. Это 8,57 доллара за метр.
• 10 досок по 6 метров каждая. Цена: 40$ за доску. Это 6,66 доллара за метр.

Самый дешевый вариант - купить 1 доску каждой на общую сумму 100$, а не покупать 3 доски самого дешевого вида на общую сумму 120$.

Что касается решения: обратите внимание на метаэвристику (поиск по Табу, имитация отжига, позднее принятие) и программное обеспечение, такое как OptaPlanner (Java, открытый исходный код).