Взвешенная оценка плотности ядра Гаусса в `python`

Question

В настоящее время невозможно использовать scipy.stats.gaussian_kde оценить плотность случайной величины на основе взвешенных выборок. Какие методы доступны для оценки плотности непрерывных случайных величин на основе взвешенных выборок?

Answer 1

Ни sklearn.neighbors.KernelDensity ни statsmodels.nonparametric кажется, поддерживают взвешенные образцы. Я модифицировал scipy.stats.gaussian_kde учесть разнородные веса выборки и полагать, что результаты могут быть полезны для других. Пример показан ниже.

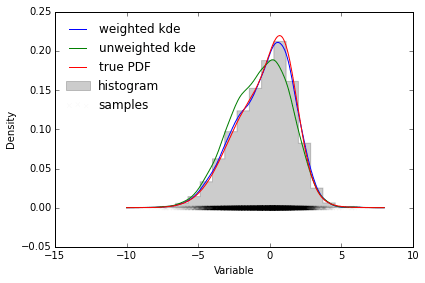
ipython блокнот можно найти здесь: http://nbviewer.ipython.org/gist/tillahoffmann/f844bce2ec264c1c8cb5

Детали реализации

Взвешенное среднее арифметическое

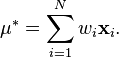
Затем несмещенная ковариационная матрица данных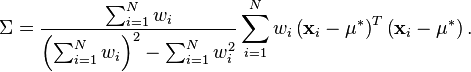

Пропускная способность может быть выбрана scott или же silverman правила как в scipy, Однако количество выборок, используемых для расчета полосы пропускания, является приближением Киша для эффективного размера выборки.

Answer 2

Для одномерных дистрибутивов вы можете использовать KDEUnivariate из statsmodels. Это не очень хорошо задокументировано, но fit методы принимают weights аргумент. Тогда вы не можете использовать БПФ. Вот пример:

import matplotlib.pyplot as plt
from statsmodels.nonparametric.kde import KDEUnivariate

kde1= KDEUnivariate(np.array([10.,10.,10.,5.]))
kde1.fit(bw=0.5)
plt.plot(kde1.support, [kde1.evaluate(xi) for xi in kde1.support],'x-')

kde1= KDEUnivariate(np.array([10.,5.]))
kde1.fit(weights=np.array([3.,1.]), 
         bw=0.5,
         fft=False)
plt.plot(kde1.support, [kde1.evaluate(xi) for xi in kde1.support], 'o-')

который производит эту цифру:

Answer 3

Проверьте пакеты PyQT-Fit и статистику для Python. Кажется, они имеют оценку плотности ядра с помощью взвешенных наблюдений.