Подгонка кривой к распределению Вейбулла в R с использованием nls

Question

Я пытаюсь приспособить эти данные к распределению Вейбулла:

мой x а также y переменные:

y <- c(1, 1, 1, 4, 7, 20, 7, 14, 19, 15, 18, 3, 4, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1)
x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24)

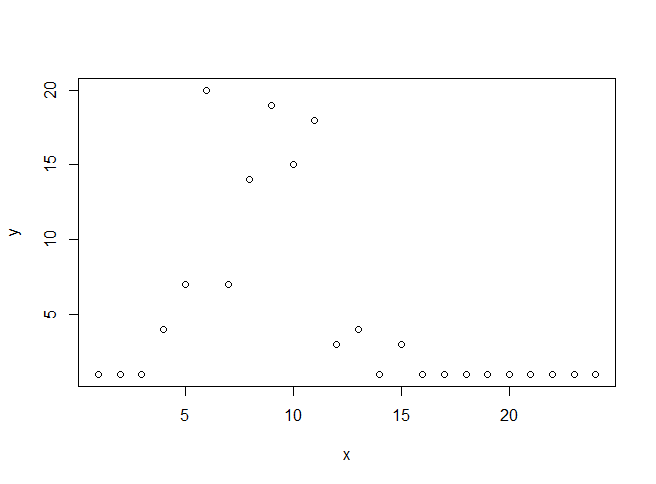
Сюжет выглядит так:

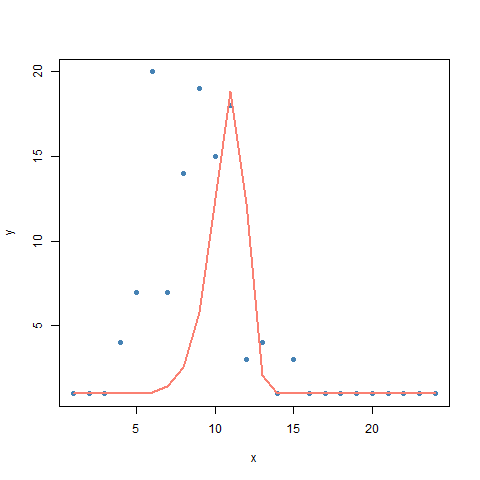
Я ищу что-то вроде этого: встроенный участок

и я хочу подогнать к нему кривую Вейбулла. Я использую функцию NLS в R, как это:

nls(y ~ ((a/b) * ((x/b)^(a-1)) * exp(- (x/b)^a)))

Эта функция всегда выдает ошибку, говорящую:

Error in numericDeriv(form[[3L]], names(ind), env) : 
  Missing value or an infinity produced when evaluating the model
In addition: Warning message:
In nls(y ~ ((a/b) * ((x/b)^(a - 1)) * exp(-(x/b)^a))) :
  No starting values specified for some parameters.
Initializing ‘a’, ‘b’ to '1.'.
Consider specifying 'start' or using a selfStart model

Итак, сначала я попробовал разные начальные значения без какого-либо успеха. Я не могу понять, как сделать "хорошее" предположение при начальных значениях. Затем я пошел с SSweibull(x, Asym, Drop, lrc, pwr) функция, которая является функцией самозапуска. Теперь функция SSWeibull ожидает значения для Asym,Drop,lrc и pwr, и я понятия не имею, какими могут быть эти значения.

Я был бы признателен, если бы кто-нибудь мог помочь мне понять, как поступить.

Справочная информация: я взял некоторые данные из bugzilla, и моя переменная "y" - это число ошибок, о которых сообщалось в конкретном месяце, а переменная "x" - это номер месяца после выпуска.

Answer 1

Вы можете рассмотреть возможность изменения формулы для лучшего соответствия данным. Например, вы можете добавить перехват (поскольку ваши данные выровнены по 1 вместо 0, что и делает модель) и скалярный множитель, поскольку вы на самом деле не подбираете плотность.

Всегда стоит потратить некоторое время на обдумывание того, какие параметры имеют смысл, потому что процедуры подбора моделей часто весьма чувствительны к первоначальным оценкам. Вы также можете выполнить поиск по сетке, где вы найдете диапазоны возможных параметров и попробуйте согласовать модель с различными комбинациями, используя функции обнаружения ошибок. nls2 имеет возможность сделать это для вас.

Так, например,

## Put the data in a data.frame
dat <- data.frame(x=x, y=y)

## Try some possible parameter combinations
library(nls2)
pars <- expand.grid(a=seq(0.1, 100, len=10),
                    b=seq(0.1, 100, len=10),
                    c=1,
                    d=seq(10, 100, len=10))

## brute-force them
## note the model has changed slightly
res <- nls2(y ~ d*((a/b) * ((x/b)^(a-1)) * exp(- (x/b)^a)) + c, data=dat,
           start=pars, algorithm='brute-force')

## use the results with another algorithm
res1 <- nls(y ~ d*((a/b) * ((x/b)^(a-1)) * exp(- (x/b)^a)) + c, data=dat,
           start=as.list(coef(res)))

## See how it looks
plot(dat, col="steelblue", pch=16)
points(dat$x, predict(res), col="salmon", type="l", lwd=2)

Не идеально, но это начало.