Лево-линейная и праволинейная грамматика

Question

Лево-линейная и праволинейная грамматика

Мне нужна помощь в построении лево-линейной и праволинейной грамматики для языков ниже?

a)  (0+1)*00(0+1)*
b)  0*(1(0+1))*
c)  (((01+10)*11)*00)*

Для а) у меня есть следующее:

Left-linear
S --> B00 | S11
B --> B0|B1|011

Right-linear
S --> 00B | 11S
B --> 0B|1B|0|1

Это правильно? Мне нужна помощь с B & C.

22

grammar regular-language computation-theory formal-languages

Источник

user1585646 11 дек '12 в 08:38

2 ответа

Решение

Правила преобразования регулярных выражений в левую или правую линейную регулярную грамматику

5

Источник

user2532763 20 янв '18 в 12:43

Другие вопросы по тегам grammar regular-language computation-theory formal-languages

user1673391 19 дек '12 в 05:13 2012-12-19 05:13 · Accepted Answer · 2012-12-19 05:13

Построение эквивалентной регулярной грамматики из регулярного выражения

Сначала я начну с нескольких простых правил построения регулярной грамматики (RG) из регулярного выражения (RE).
Я пишу правила для правой линейной грамматики (оставляя в качестве упражнения написание аналогичных правил для левой линейной грамматики)

ПРИМЕЧАНИЕ: заглавные буквы используются для переменных, и маленькие для терминалов в грамматике. NULL символ ^, Термин "любое число" означает ноль или более раз, которые означают * закрытие звезды.

[ ОСНОВНАЯ ИДЕЯ ]

ОДИНОЧНЫЙ ТЕРМИНАЛ: если RE просто e (e being any terminal) мы можем написать G только с одним правилом производства S --> e (где S is the start symbol), является эквивалентом RG.
РАБОТА СОЮЗА: если RE имеет форму e + f где оба e and f are terminals мы можем написать G с двумя правилами производства S --> e | f, является эквивалентом RG.
КОНКАТЕНЦИЯ: если RE имеет форму ef где оба e and f are terminals мы можем написать G с двумя правилами производства S --> eA, A --> f, является эквивалентом RG.
ЗАКРЫТИЕ ЗВЕЗДЫ: Если RE имеет форму e*, где e is a terminal а также * Kleene star closure операции, мы можем написать два правила производства в G, S --> eS | ^, является эквивалентом RG.
ПЛЮС ЗАКРЫТИЕ: если RE имеет форму е ⁺, где e is a terminal а также + Kleene plus closure операции, мы можем написать два правила производства в G, S --> eS | e, является эквивалентом RG.
ЗАКРЫТИЕ ЗВЕЗДЫ НА СОЮЗЕ: Если RE имеет форму (e + f)*, где оба e and f are terminals мы можем написать три правила производства в G, S --> eS | fS | ^, является эквивалентом RG.
ПЛЮС ЗАКРЫТИЕ НА СОЮЗЕ: Если RE имеет форму (e + f) ⁺, где оба e and f are terminals мы можем написать четыре правила производства в G, S --> eS | fS | e | f, является эквивалентом RG.
ЗАКРЫТИЕ ЗВЕЗДЫ НА КОНКАТЕНЦИИ: Если RE имеет форму (ef)*, где оба e and f are terminals мы можем написать три правила производства в G, S --> eA | ^, A --> fS, является эквивалентом RG.
ПЛЮС ЗАКРЫТИЕ НА КОНКАТЕНЦИИ: Если RE имеет форму (ef) ⁺, где оба e and f are terminals мы можем написать три правила производства в G, S --> eA, A --> fS | f, является эквивалентом RG.

Убедитесь, что вы понимаете все вышеперечисленные правила, вот сводная таблица:

+-------------------------------+--------------------+------------------------+
| TYPE                          | REGULAR-EXPRESSION | RIGHT-LINEAR-GRAMMAR   |
+-------------------------------+--------------------+------------------------+
| SINGLE TERMINAL               | e                  | S --> e                |
| UNION OPERATION               | e + f              | S --> e | f            |
| CONCATENATION                 | ef                 | S --> eA, A --> f      |
| STAR CLOSURE                  | e*                 | S --> eS | ^           |
| PLUS CLOSURE                  | e+                 | S --> eS | e           |
| STAR CLOSURE ON UNION         | (e + f)*           | S --> eS | fS | ^      |
| PLUS CLOSURE ON UNION         | (e + f)+           | S --> eS | fS | e | f  |
| STAR CLOSURE ON CONCATENATION | (ef)*              | S --> eA | ^, A --> fS |
| PLUS CLOSURE ON CONCATENATION | (ef)+              | S --> eA, A --> fS | f |
+-------------------------------+--------------------+------------------------+

примечание: символ e а также f являются терминалами, ^ является нулевым символом, и S переменная начала

[ОТВЕТ]

Теперь мы можем прийти к вам проблемы.

а) (0+1)*00(0+1)*

Описание языка: Все строки состоят из 0 и 1, содержащие как минимум одну пару 00,

Правильная линейная грамматика:
S -> 0S | 1S | 00A
A -> 0A | 1А | ^
Строка может начинаться с любой строки 0 с и 1 Вот почему включены правила s --> 0S | 1S и потому, что по крайней мере одна пара 00, нет нулевого символа. S --> 00A включен, потому что 0, 1 может быть после 00, Символ A заботится о 0 и 1 после 00,
Левая линейная грамматика:
S -> S0 | S1 | A00
A -> A0 | A1 | ^

б) 0*(1(0+1))*

Описание языка: любое число от 0 до 10 и 11.
{потому что 1(0 + 1) = 10 + 11 }

Правильная линейная грамматика:
S -> 0S | A | ^
A -> 1B
B -> 0A | 1А | 0 | 1
Строка начинается с любого числа 0 так правило S --> 0S | ^ включены, то правило для генерации 10 а также 11 за любое количество раз, используя A --> 1B and B --> 0A | 1A | 0 | 1,
Другая альтернативная правая линейная грамматика может быть
S -> 0S | A | ^
A -> 10A | 11А | 10 | 11
Левая линейная грамматика:
S -> A | ^
A -> A10 | A11 | В
B -> B0 | 0
Альтернативная форма может быть
S -> S10 | S11 | Б | ^
B -> B0 | 0

с) (((01+10)*11)*00)*

Описание языка: Во-первых, язык содержит пустую строку (^), потому что внутри каждой вещи, присутствующей внутри (), есть * (звезда). Кроме того, если строка в языке не является нулевой, которая демонстративно заканчивается на 00. Можно просто думать, что это регулярное выражение в виде ( ( (A)* B)* C)*, где (A) * равно (01 + 10)* это любое число повторений от 01 до 10. Если в строке есть экземпляр A, то будет вызывающе B, потому что (A) * B и B равно 11.
Некоторые примеры строк { ^, 00, 0000, 000000, 1100, 111100, 1100111100, 011100, 101100, 01110000, 01101100, 0101011010101100, 101001110001101100 ....}

Левая линейная грамматика:
S -> A00 | ^
A -> B11 | S
B -> B01 | B10 |
S --> A00 | ^ потому что любая строка либо нулевая, либо, если она не нулевая, она заканчивается 00, Когда строка заканчивается 00 переменная A соответствует шаблону ((01 + 10)* + 11)*, Опять же, этот шаблон может быть либо нулевым, либо должен заканчиваться 11, Если его ноль, то A совпадает с S опять то есть строка заканчивается шаблоном как (00)*, Если шаблон не является нулевым, B соответствует (01 + 10)*, когда B соответствует все, что может, A начинает сопоставлять строку снова. Это закрывает самый-самый * в ((01 + 10)* + 11)*,
Правильная линейная грамматика:
S -> A | 00S | ^
A -> 01A | 10А | 11S

Вторая часть вашего вопроса:

For a) I have the following:
Left-linear
S --> B00 | S11
B --> B0|B1|011

Right-linear
S --> 00B | 11S
B --> 0B|1B|0|1

(ответ)
Ваше решение неверно по следующим причинам,

Левая линейная грамматика неверна, потому что строка 0010 не возможно генерировать. Правильно-линейная грамматика неверна, потому что строка 1000 не возможно генерировать. Хотя оба языка написаны регулярным выражением вопроса (а).

РЕДАКТИРОВАТЬ
Добавление DFA для каждого регулярного выражения. так что можно найти это полезным.

а) (0+1)*00(0+1)*

DFA

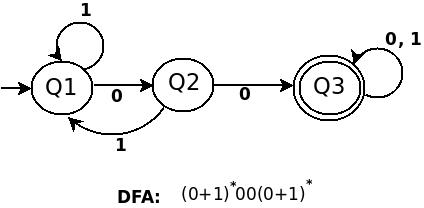
б) 0*(1(0+1))*

DFA

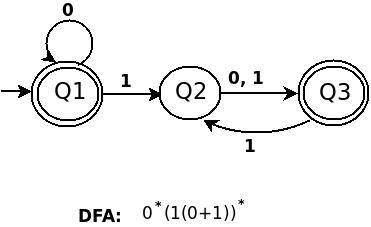
с) (((01+10)*11)*00)*

Рисование DFA для этого регулярного выражения является хитрым и сложным.
_{Для этого я хотел добавить DFA's}

Чтобы упростить задачу, нам следует подумать о том, как мне нужно сформировать своеобразие RE. (((01+10)*11)*00)* похоже (a*b)*

(((01+10)*11)* 00 )*
(          a*   b )*

На самом деле в выражении выше a это само в форме (a*b)* то есть ((01+10)*11)*

RE (a*b)* равно (a + b)*b + ^, DFA для (a b) является следующим:

DFA

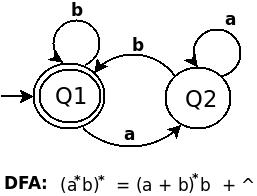
ДФА для ((01+10)*11)* является:

DFA

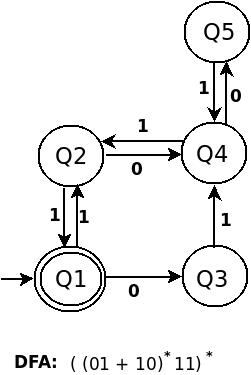
ДФА для (((01+10)*11)* 00 )* является:

DFA

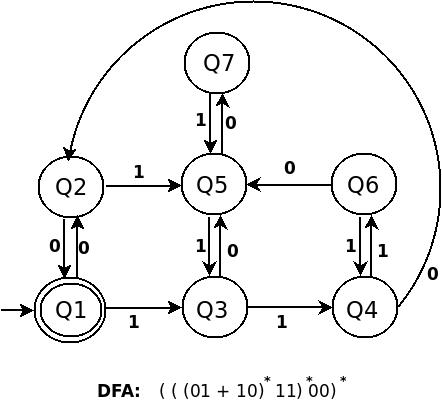
_{Попробуйте найти сходство в построении выше трех DFA.} _{не двигайтесь вперед, пока не поймете первый}